Чистый сдвиг и его особенности

Сдвиг

Сдвиг, КРУЧЕНИЕ

Сдвигом называется такой вид нагружения, при котором в поперечных сечениях бруса из шести внутренних усилий отличными от нуля являются только поперечные силы.

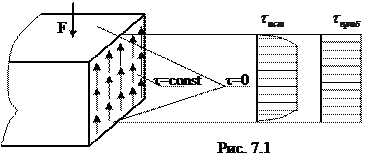Такой вид нагружения встречается редко. Чаще всего он сопровождается изгибающими мо-ментами. Однако, в некоторых случаях, например, в заклёпочных, болтовых, сварных сое-динениях имеет место нагружение близкое к сдвигу. При этом распределение касательных напряжений неравномерно. Так как внешние поверхности свободны от осевых нагрузок, топо закону парности касательных напряжений в верхних и нижних точках сечения 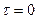. Из уравнения равновесия следует 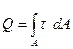. Как показывают исследования, распределение 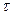по высоте сечения близко к равномерному (τ=const), поэтому 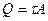и 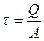, где А – площадь среза.

Условие прочности: 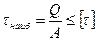, (7.1)

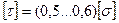- для пластических материалов и 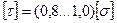- для хрупких материалов.

Чистым сдвигом называется такой вид плоского напряженного состояния, при котором по граням элементарного параллелепипеда, выделенного в окрестности рассматриваемой точки, действуют одни лишь касательные напряжения.

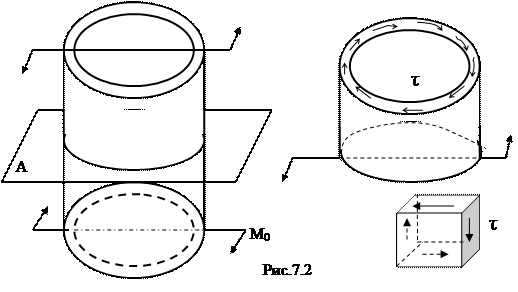
В качестве примера такого напряженного состояния можно рассмотреть тонкостенную цилиндрическую трубку, нагруженную по торцам парами сил (рис.7.2). Рассечем её плоскостью А, отбросим верхнюю часть и покажем оставшуюся нижнюю часть. В сечении действуют касательные напряжения τ, величина которых определится из условия равенства момента равномерно распределенных по сечению внутренних сил внешнему моменту М₀: 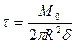, где R – средний радиус трубки, δ – её толщина.

Нормальных напряжений в этом сечении не будет. Вырежем из стенки бесконечно малый элемент в виде кубика. На его нижней грани будут действовать касательные напряжения такие же, как и на верхней, но в противоположном направлении. На передней и задней стенках напряжений нет. Так как элемент должен находиться в равновесии, то на боковых стенках также должны быть касательные напряжения, которые создают пару сил, но направленную в противоположную сторону.

При чистом сдвиге длины ребер элементарного параллелепипеда не изменяются, а изменяются углы между гранями (рис. 7.3). Верхняя грань параллелепипеда перемещается относительно противоположной грани на величину δ, называемую абсолютным сдвигом.

маций tgγ = γ, тогда 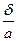= γ(рад).

Как показывает опыт, угол сдвига γ прямо пропорционален касательным напряжениям. Эта зависимость между γ и τ называется законом Гука при сдвиге и записывается выражением

, или 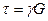. (7.2)

Коэффициент пропорциональности G называется модулем сдвига (или модулем упругости второго рода). Он как и модуль продольной упругости Е измеряется в паскалях (Па) или в мегапаскалях (МПа).

Дата добавления: 2014-10-23