Пример. Инвариантное управление

Инвариантное управление.

Как отмечалось в разделе 8, ошибка регулирования зависит от точности воспроизведения задающего воздействия и влияния на выходную координату внешних воздействий. Рассмотрим системы управления, которые позволяют полностью или частично компенсировать ошибки регулирования, т.е. системы инвариантного управления.

Ошибка регулирования по заданию и возмущению были получены в разделе 8 и равны соответственно:

ошибка по воспроизведению задания:

(9.14)

,

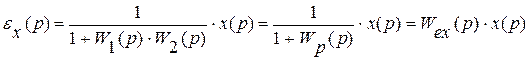ошибка по возмущению:

(9.15)

.

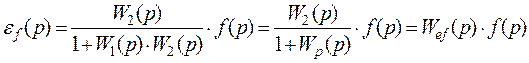Как видно, ошибка регулирования будет зависеть как параметров самой системы, так и от входного и возмущающих воздействий.

Точность систем можно повысить путем компенсации влияния сигналов задания и возмущения за счет применения комбинированного управления. При полной компенсации система получается полностью инвариантна к внешним воздействиям. При этом повышается порядок астатизма.

Системы, инвариантные по заданию.

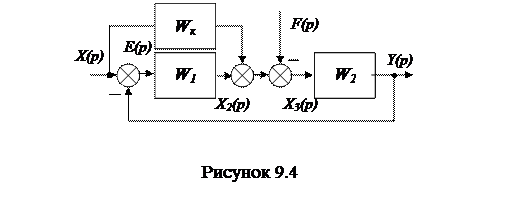Рассмотрим параллельную коррекцию, введенную в систему по заданию (рисунок 9.4).

Положим, что F(p)=0. Тогда:

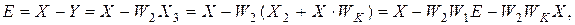
Отсюда:

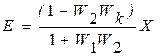. (9.16)

Для того, чтобы ошибка была бы равна нулю, необходимо 1- W₂W_k =0, или условием инвариантности системы по заданию является уравнение:

(9.5)

_. (9.17)

Чем больше порядок передаточной функции звена W ₂, тем сложнее реализовать корректирующее инвариантное звено. Поэтому при большой сложности W ₂ удовлетворяются частичные условия. При этом система не будет полностью инвариантна к задающему воздействию. Так на практике чаще всего используют такие звенья, которые позволяют скорректировать статическую ошибку и скоростную ошибку.

Системы, инвариантные к возмущению.

Рассмотрим параллельную коррекцию, введенную в систему по возмущению (рисунок 9.5).

Требуется выбрать такое корректирующее звено W _к, чтобы ошибка

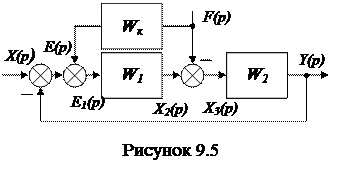по возмущению была бы равна 0.

Будем считать, что задающее воздействие равна нулю. Выведем зависимость ошибки регулирования от возмущения.

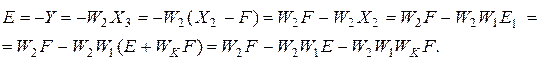(9.18)

Отсюда:

(9.19)

.

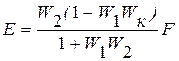Условием инвариантности системы по возмущению является уравнение:

(9.6)

_.

(9.7)

. (9.20)

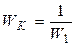Для систем, инвариантных по возмущающему воздействию накладываются такие же ограничения по реализуемости корректирующего звена.

Пусть система имеет структуру как показано на рисунке 9.6.

Ошибка нескорректированной системы по возмущению будет иметь вид:

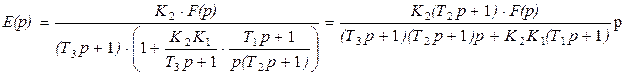
Как видно система будет иметь порядок астатизма равный 1 (т.е. система будет астатична только в статическом режиме).

При полной инвариантности по возмущению передаточная функция корректирующего звена должна иметь вид (см. формулу 9.20):

.

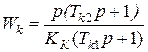где =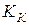

= ,

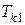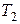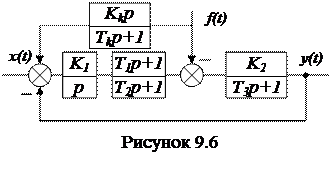
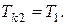
Из-за сложности реализации такого звена сделаем упрощение:

.

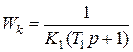Ошибка скорректированной системы из (9.19):

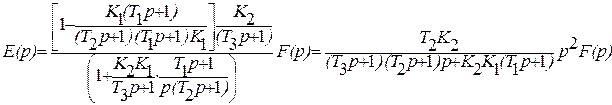
Порядок астатизма увеличился на единицу (т.о. ошибка по положению и по скорости будет равна нулю).

Чаще всего на практике передаточную функцию корректирующего звена выбирают такой, чтобы скомпенсировать ошибки в статическом режиме и скоростную ошибку.

Инвариантное управление используют чаще всего в системах, где ставится требование к высокой точности выходной координаты (например. в следящих системах).

Дата добавления: 2014-10-23