Эмиссия электронов из твердого тела

ПО ПРЯМЫМ РИЧАРДСОНА

ОПРЕДЕЛЕНИЕ РАБОТЫ ВЫХОДА ЭЛЕКТРОНА

ЛАБОРАТОРНАЯ РАБОТА № 5

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Существует ряд возможностей стимуляции эмиссии свободных электронов, в особенности металлов. В техническом отношении главную роль играет термоэлектронная эмиссия, получаемая с помощью накальных (термоэлектронных) катодов.

Термоэлектронная эмиссия

Металлические накальные катоды

Потенциальный барьер, существующий на границе любого металлического тела, препятствует свободному выходу электронов из металла. Это весьма наглядно демонстрирует модель потенциальной ямы, предложенная Шоттки, со всеми вытекающими из нее следствиями. Поэтому необходимо принять специальные меры, чтобы электроны из металла смогли преодолеть этот барьер. При термоэлектронной эмиссии это достигается путем увеличения кинетической энергии электронов за счет нагрева катода. Поскольку распределение кинетической энергии электронов в металле известно (распределение Ферми), можно рассчитать плотность тока на накальном катоде при заданной температуре. При этом нужно учитывать следующие обстоятельства. Поскольку температура отлична от нуля, распределение Ферми изменяется таким образом, что уровень Ферми теперь уже не является четкой верхней границей для энергии электронов. В принципе могут существовать электроны с энергией, лежащей сколь угодно выше уровня Ферми, причем вероятность этого тем больше, чем выше температура катода. Если энергия электрона станет равной энергии выхода, то электрон может покинуть металл. В механике аналогом потенциального барьера на границе металл - вакуум служит поле тяжести Земли. Например, чтобы перекинуть мяч через стенку, ему необходимо сообщить кинетическую энергию, по меньшей мере равную потенциальной энергии мяча, лежащего на стенке сверху. Если кинетическая энергия будет для этого недостаточна, то мяч упадет обратно. Если она будет больше указанной, то мяч не только преодолеет стенку, но и, преодолев ее, будет обладать определенной скоростью. Условие перелета мяча через стенку можно записать следующим образом:

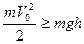, (1)

где 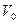- начальная скорость мяча, 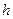- высота стенки, 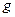- ускорение свободного падения. Разумеется, начальная скорость 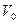должна быть направлена вертикально вверх, т. е. против силы тяжести, поскольку при броске под угломк горизонту потребовалась более высокая скорость, так как эффект определяется только вертикальной компонентой .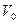

В случае выхода электронов из потенциальной ямы металла это означает, что следует учитывать только перпендикулярную стенке компоненту скорости 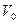, т. е. компоненту 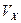, если направление 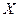перпендикулярно барьеру. Поэтому нужно подсчитать, сколько электронов в электронном газе (ферми-газе) внутри металла обладают 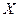-компонентой скорости, превышающей значение, при которой кинетическая энергия электрона равна работе выхода. Чтобы ответить на этот вопрос, нужно использовать полученное ранее распределение Ферми:

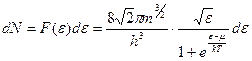, (2)

где 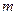- масса электрона, 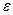- кинетическая энергия электрона, 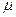- энергия Ферми, 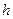- постоянная Планка, - абсолютная температура и преобразовать его таким образом, чтобы выделить распределение по отдельным компонентам скорости. Для этого рассмотрим пространство скоростей, т. е. трехмерное пространство, координатами которого являются три взаимно перпендикулярные компоненты скорости. Электрон, движущийся со скоростью 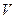, изображается в этой системе координат точкой с координатами 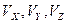. Распределение Ферми (2) описывает совокупность точек, отражающих все электроны, кинетические энергии которых заключены между 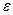и 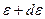. Эти точки лежат внутри шарового слоя, ограниченного поверхностями с радиусам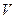и и 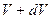, причем

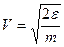и .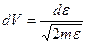

Объем этого шарового слоя равен

.

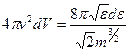В силу сферической симметрии уравнения, описывающего распределения по энергиям, точки заполняют этот объем равномерно с одинаковой плотностью. Разделив выражение (2) на этот объем и умножив на элементарный объем 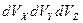, получим число электронов, для которых изображающие точки в пространстве скоростей содержатся в этом элементарном объеме, а компоненты скоростей – в област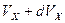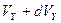и , и 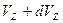. Эта величина необходима для решения нашей задачи. Она равна

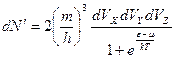, (3)

где .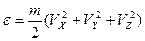

Для электронов, тепловая энергия которых достаточна для того, чтобы они могли выйти из металла, должно лишь выполняться требование 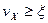, в то время как на две другие компоненты скорости не накладывается никаких ограничений. Минимальную скорость 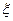можно рассчитать исходя из энергетического соотношения

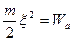, (4)

где 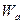- разность энергий, соответствующих дну потенциальной ямы и ее краю.

Если в единице объема содержится 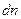электронов, 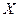-компоненты скоростей которых лежат между 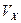и 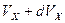и удовлетворяют условию , то именно эта группа электронов определяет плотность эмиссионного тока

.

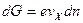Для полной плотности тока с учетом выражения (3) получаем

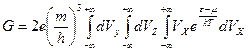, (5)

здесь учтено, что при 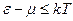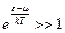. Интегрируя, находим, наконец, для 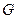соотношение:

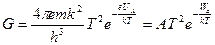, (6)

которое называется формулой Ричардсона. Здесь 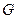- максимальная плотность электронного тока, которую может дать накальный катод при температуре (плотность тока насыщения). Так называемая постоянная Ричардсона рассчитывается следующим образом:

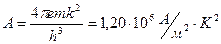, (7)

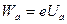- работа выхода. Ее связь с глубиной 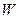потенциальной ямы и уровнем Ферми 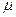можно найти по рис. 1. Легко видеть, что

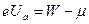. (8)

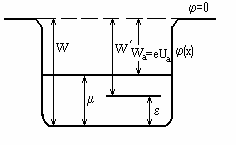
Рис. 1. Модель распределения потенциала в металле по Шоттки (потенциальная яма)

Формулу (6) можно непосредственно проверить экспериментально. Для рассмотрения результатов лучше всего построить график зависимости 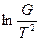от 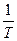. Тогда согласно формуле (6) должна получиться прямая (прямая Ричардсона), по наклону которой можно определить работу выхода. Если же экстраполировать прямую на 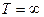, то отрезок, отсекаемый ею на оси ординат, будет равен .

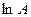Работа выхода чистых металлов, измеренная таким образом, составляет несколько электрон-вольт. У вольфрама, который благодаря своей теплостойкости имеет большое значение как материал для накальных катодов и на котором поэтому часто проводят измерения, работа выхода равна 4,52 эВ.

Работа выхода чистых металлов несколько зависит от температуры: она линейно возрастает с ростом температуры. Это связано с двумя причинами. Во-первых, положение уровня Ферми 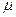зависит от , а именно более точный расчет дает для 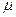выражение в виде ряда

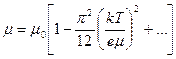. (9)

Однако описываемая этим выражением зависимость от несущественна, и ею в большинстве случаев можно пренебречь. Во-вторых, термическое расширение металла по мере повышения температуры вызывает уменьшение концентрации электронов и, следовательно, приводит к понижению уровня Ферми 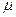. Однако согласно (8) уровень Ферми связан с работой выхода таким образом, что повышение температуры будет вызывать незначительное увеличение работы выхода. Теория и эксперимент, например, для вольфрама дают значение .

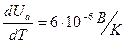Значение постоянной Ричардсона 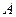, найденной путем измерений, всегда вытекающих из теории, равно 120 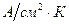. Это обусловлено двумя причинами. Лежащее в основе вывода формулы (6) условие 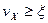является необходимым, но не достаточным. Электроны, удовлетворяющие этому условию, не обязательно выйдут из металла в вакуум, а могут отразиться от поверхности раздела между ними и вновь вернуться внутрь металла. Ввиду того что эти электроны не могут быть обнаружены как ток эмиссии, значение постоянной 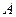снижается. В вольфраме доля отраженных электронов составляет 50%, так что величина 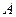будет вдвое меньше значения (7). Для объяснения этой ситуации целесообразно снова обратиться к волновому представлению об электроне и привлечь к рассмотрению известные оптические явления. Луч света, попадающий на оптическую неоднородность (границу раздела), например на границу между воздухом и стеклом, не полностью переходит из одной среды в другую, а частично отражается, причем доля отраженного света зависит от показателя преломления. То же происходит с отраженной волной, идущей из металла и достигающей поверхности. Аналогично можно продолжить еще дальше. Если на поверхность, на которую падает световой луч, нанести покрытие, например напыленную тонкую металлическую пленку, то отражение будет существенно возрастать до тех пор, пока, наконец, при достаточной толщине покрытия не начнет отражаться весь свет, т. е. получится идеальное зеркало, вообще не пропускающее света. В соответствии с этим можно ожидать, что при термоэлектронной эмиссии наличие на первоначально чистой металлической поверхности какого-либо чужеродного слоя будет увеличивать число отраженных от поверхности электронов, т. е. постоянная Ричардсона 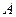будет уменьшаться. Этот вывод находится в согласии с результатами измерений, которые показывают, что постоянная 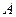всегда уменьшается, если вместо чистого металлического катода используется катод с покрытием, например торий на вольфраме, оксидный катод и т.п.

Другой причиной того, что измеренное значение постоянной Ричардсона ниже теоретического, является указанная температурная зависимость работы выхода: 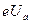слегка возрастает с температурой. В первом приближении для 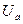оказывается справедливой линейная зависимость 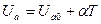, причем у металлов температурный коэффициент по порядку величины составляет 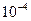. Если температурную зависимость работы выхода ввести в формулу Ричардсона, то из (6) находим

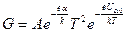. (10)

Отсюда сразу же получаем (при положительном значении 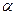) уменьшение постоянной .

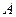Эффект Шоттки

Если вакуумный диод включить не в обратном, а в прямом направлении, т. е. приложить положительное анодное напряжение, то можно заметить следующее. Согласно формуле (6) ток не должен зависеть от анодного напряжения, поскольку оно даже не входит в формулу Ричардсона – Дэшмана. Однако в действительности всегда наблюдается возрастание тока при увеличении напряжения, и только начиная с определенного значения 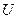, которое зависит от геометрии межэлектродного зазора диода, ток имеет постоянную величину, соответствующую получающейся по формуле (6). Таким образом, лишь этот ток насыщения можно использовать для определения работы выхода и постоянной 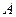с помощью описанных методов. Однако и ток насыщения также не остается все время постоянным; при достаточно большом анодном напряжении снова начинается, хотя и медленное, увеличение тока при возрастании напряжения. Это возрастание тока, называемое эффектом Шоттки, можно наглядно объяснить исходя из модели потенциальной ямы, если одновременно рассмотреть ход потенциала в вакуумном промежутке, как показано на рис. 2. Как видно из него, поле в вакуумном промежутке получается в результате наложения создаваемого анодом поля (которое, например, между плоскопараллельными электродами однородно) и поля, притягивающего электрон, выходящий на катод. На достаточном расстоянии от катода это поле можно представить как поле сил изображения, потенциал которого, как показывает расчет, равен 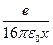. Таким образом, получаем следующее выражение для суммарного потенциала между пластинами:

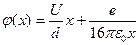, (11)

где 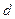- расстояние между пластинами. Потенциал 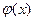имеет минимум (положительный потенциал на рис. 2 откладывается вниз), положение 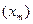и величину 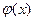которого можно рассчитать следующим образом:

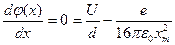
и при :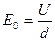

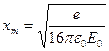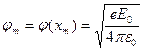, . (12)

Как следует из рис. 2, работа выхода 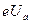уменьшается на 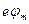, так как потенциальный барьер, препятствующий выходу электронов, снижается на величину 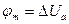. За счет воздействия поля анода край потенциальной ямы изгибается вниз. Плотность тока эмиссии по-прежнему определяется формулой Ричардсона – Дэшмана, только вместо работы выхода 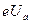нужно поставить уменьшенное значение этой величины 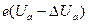. Благодаря этому ток возрастает в 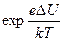раз по сравнению с током, который существовал бы при исчезающей малой напряженности приложенного поля.

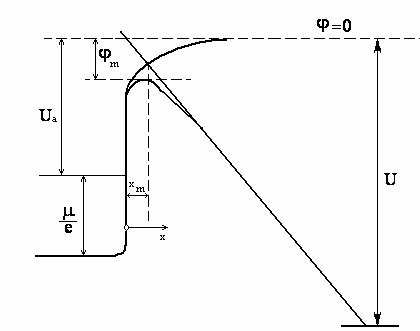
Рис. 2. К теоретическому рассмотрению эффекта Шоттки

Логарифмируя формулу (10), получим:

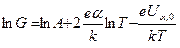, (14)

или

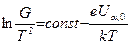. (15)

Построив график зависимости lnG/T²) = f(1/T), получим прямую линию (прямую Ричардсона), угловой коэффициент которой равен 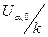. Отсюда можно найти значение .

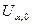В задаче используется вакуумная лампа 2Ц2С с вольфрамовым катодом. Катод нагревается постоянным током. Величина тока регулируется реостатом в цепи накала. Амперметр и вольтметр в этой цепи служат для определения сопротивления катода, величина которого необходима для определения температуры катода (см. табл. 2). Площадь поверхности катода для лампы 2Ц2С равна 0.54 см². Сопротивление катода лампы при T = 273⁰K составляет 0,307 Ом. При выполнении работы необходимо учитывать, что анодный ток равен току эмиссии лишь в режиме насыщения и для каждого тока накала анодное напряжение должно быть равно U_нас. Температура катода определяется по данным таблицы.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

1. Собрать схему для измерений по рис. 3. Познакомиться с классом точности каждого прибора.

2. Изучить зависимость анодного тока от анодного напряжения при токах накала 1,2; 1,3А и построить соответствующие графики.

3. Получить данные о зависимости тока эмиссии от температуры катода при токах накала 1,2 - 1,35 А и построить график зависимости плотности термоэлектрического тока от температуры катода. При измерениях следует изменять ток накала так, чтобы ток эмиссии возрастал каждый раз на 20 - 30%.

4. Построить график зависимости ln G/T² от 1/T и рассчитать по нему значение работы выхода электрона из вольфрама.

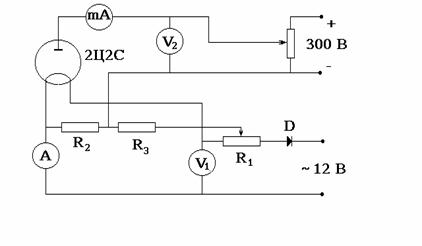
Рис. 3. Схема установки

Л - лампа 2Ц2С; mA - миллиамперметр с пределами 1mA и 7,5mA; V₂ - вольтметр 300В; R₂ = R₃ = 80 Ом; V₁ - вольтметр 3В; R₁ - реостат 33 Ом;

Д - диод.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. Что такое работа выхода электрона?

2. Из каких теоретических предпосылок можно определить работу выхода?

3. Нарисуйте схему установки для определения работы выхода и объясните её работу.

4. Выведите уравнение термоэлектронной эмиссии.

5. Какую информацию о строении твердых тел можно получить из данных по работе выхода?

6. Какова вольт-амперная характеристика вакуумного диода при различных температурах?

7. Какова вольт-амперная характеристика полупроводникового диода?

Таблица

Зависимость относительного сопротивления вольфрама от температуры.

T, ^0K	R/R273	T, ^0K	R/R273	T, ^0K	R/R273
	1.12 1.50 2.07 2.59 3.11 3.65 4.21 4.78 5.36 5.95 6.65		7.16 7.78 8.41 9.04 9.69 10.34 11.00 11.65 12.33 13.01 13.69		14.38 15.08 16.48 17.19 17.90 18.62 19.35 20.06 20.83 21.56 22.30

Дата добавления: 2014-10-23