Алгоритм построения проекций отрезка прямой линии

Построение комплексного чертежа прямой линии

Координаты точек

Пример решения типовой задачи

Задача 1. Даны координаты X, Y, Z точек A,B,C,D,E,F (табл. 3.3)

Таблица 3.3

Ось	A	B	C	D	E	F
X				–20		–10
Y		–50		–30
Z		–40

По заданным координатам построить наглядное изображение и комплексный чертёж точек A, B, C, D, E, F в системе плоскостей проекций П₁П₂П₃.

Алгоритм решения.

1. Проанализировать координаты точки, соотнося знаки координат с осями координат.

2. Определить четверть, в которой расположена точка.

3. Построить наглядное изображение системы трех плоскостей проекций (рис. 3.2).

4. Следовать этапам алгоритма построения наглядного изображения точки и ее проекций по координатам (табл. 3.1).

5. Построить комплексный чертеж системы трех плоскостей проекций (табл. 3.2).

4. КОМПЛЕКСНЫЙ ЧЕРТЁЖ ПРЯМОЙ ЛИНИИ

Прямая линия определяется двумя принадлежащими ей точками, которые задаются на чертеже своими проекциями. Таким образом, для получения комплексного чертежа прямой достаточно построить проекции двух её точек и соединить одноимённые проекции между собой: горизонтальную [А₁В₁], фронтальную [А₂В₂] и профильную [А₃В₃] проекции прямой линии.
В табл. 4.1 дан алгоритм построения комплексного чертежа отрезка прямой линии по координатам двух её точек.

Таблица 4.1

Словесная форма	Графическая форма
1. Отложить значения координат для точек А и В на осях x, y, z. Получаем вспомогательные точки: Ax, Bx на оси OX; Aу, By на оси OY; Az Bz на оси OZ. При построении этих точек необходимо учитывать знаки координат и откладывать их на осях в соответствующем направлении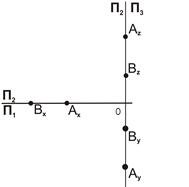
2. Построить проекции точек А и В: А1(x; y), В1(x; y); А2(x; z), В2 (x;z). 3. Соединить соответствующие проекции точек А1 с В1, А2 с В2. Получаем проекции отрезка АВ: [А1В1] и [А2В2]. [А1В1] – это проекция отрезка прямой линии на П1. [А2В2] – это проекция отрезка прямой линии на П2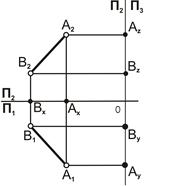
4. Отложить значение координаты Y на оси OY профильной плоскости: Ay By, где A3(y; z), B3 (y; z)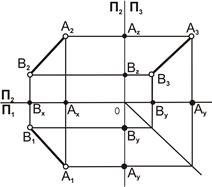

4.2. Положение прямой линии относительно
плоскостей проекций

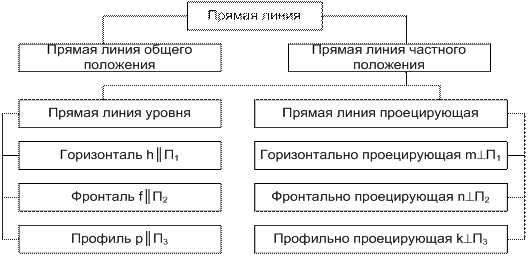
По положению прямой линии относительно плоскостей проекций различают прямые общего положения и частного положения (рис. 4.1).

Рис. 4.1. Классификация прямых линий

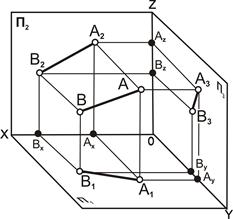
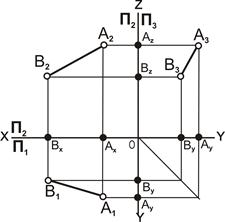
Прямая линия общего положения не параллельная ни одной из плоскостей проекций. В системе плоскостей проекций П₁П₂П₃ прямая АВ будет иметь следующие проекции: [А₁В₁] на П₁, [А₂В₂] на П₂, и [А₃В₃] на П₃ (рис. 4.2).

а	б
Рис. 4.2. Прямая линия общего положения: а – наглядное изображение; б – комплексный чертёж

Прямая линия частного положения – прямая, параллельная либо перпендикулярная одной из плоскостей проекций.

Прямая линия уровня – прямая, параллельная одной из плоскостей проекций: горизонтали, фронтали, профильной прямой.

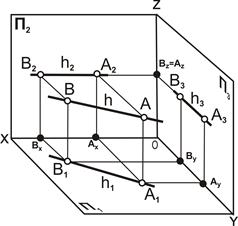
Горизонталь h – прямая линия, параллельная горизонтальной плоскости проекций П₁ (рис. 4.3).

Свойства проекций горизонтали.

1. Проекция прямой линии h₁(A₁B₁) равна самому отрезку, [A₁B₁]=|AB|.

2. Фронтальная и профильная проекции параллельны осям проекций, h₂[А₂В₂]II Ox, [A₃B₃]IIOY.

3. Угол наклона β к плоскости П₂ проецируется в натуральную величину на плоскость П₁.

4. На комплексном чертеже определяется двумя проекциями h₁, h₂.

а	б
Рис. 4.3. Горизонталь h: а – наглядное изображение; б – комплексный чертёж

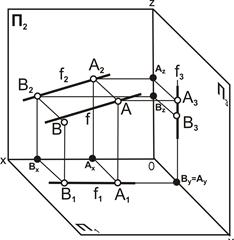
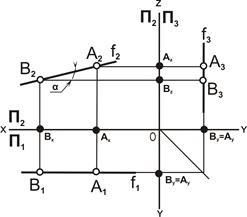
Фронталь f – прямая линия, параллельная фронтальной плоскости проекций П₂ (рис. 4.4).

Свойства проекций фронтали.

1. Проекция фронтали f₂(A₂B₂) равна самому отрезку, [A₂B₂]=|AB|.

2. Горизонтальная и профильная проекции параллельны осям проекций: [А₁В₁]II Ox,[A₃B₃]IIOZ.

3. Угол наклона a к плоскости П₁ проецируется в натуральную величину на плоскость П₂.

4. На комплексном чертеже определяется двумя проекциями f₁, f₂.

а	б
Рис. 4.4. Фронталь f: а – наглядное изображение; б – комплексный чертёж

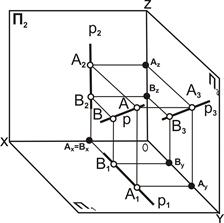
Профильная прямая р – это прямая линия, параллельная профильной плоскости проекций П₃ (рис. 4.5).

Свойства проекций профильной прямой.

1. Проекция профильной прямой p₃(A₃B₃) равна самому отрезку, [A₃B₃]=|AB|.

2. Горизонтальная и фронтальная проекции параллельны осям проекций: [А₁В₁]II y, [A₂B₂]IIOZ.

3. Углы наклона a и β проецируются в натуральную величину на плоскость П₃.

4. На комплексном чертеже определяется двумя проекциями p₂, p₃.

а	б
Рис. 4.5. Профильная прямая p: а – наглядное изображение; б – комплексный чертёж

Проецирующая прямая линия – это прямая, перпендикулярная плоскости проекций.

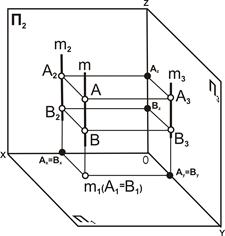
Горизонтально проецирующая прямая – прямая, перпендикулярная горизонтальной плоскости проекций П₁ (рис. 4.6).

а	б
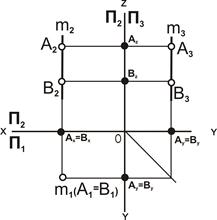
Рис. 4.6. Горизонтально проецирующая прямая: а – наглядное изображение; б – комплексный чертёж

Свойства проекций горизонтально проецирующей прямой.

1. Проекция прямой линии m₂(A₁B₁) вырождается в точку, А₁=В₁.

2. Проекция m₂(А₂В₂) параллельна линиям связи.

3. Горизонтально проецирующая прямая параллельна одновременно П₂ и П₃, следовательно, [А₂В₂] = [А₃В₃] = |АВ|.

Фронтально проецирующая прямая – прямая линия, перпендикулярная фронтальной плоскости проекций П₂ (рис. 4.7).

а	б
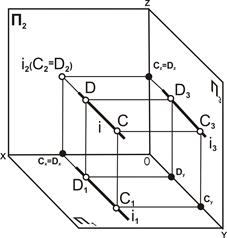
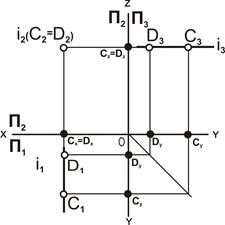
Рис. 4.7. Фронтально проецирующая прямая: а – наглядное изображение; б – комплексный чертёж

Свойства проекций фронтально проецирующей прямой.

1. Проекция прямой линии i₂(С₂D₂) вырождается в точку, C₂=D₂.

2. Проекция i₁(С₁D₁) и проекция i₃(С₃D₃) параллельны линиям связи.

3. Фронтально проецирующая прямая параллельна одновременно П₁ и П₃, следовательно, [C₁D₁] = [C₃D₃] = |CD|.

Профильно проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций П₃ (рис. 4.8).

а	б
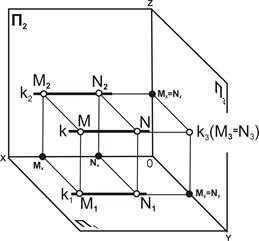
Рис. 4.8. Профильно проецирующая прямая: а – наглядное изображение; б – комплексный чертёж

Свойства проекций профильно проецирующей прямой.

1. Проекция прямой линии k₃(M₃N₃) вырождается в точку, M₃=N₃.

2. Горизонтальная k₁(M₁N₁) и фронтальная k₂(M₂N₂) проекции перпендикулярны линиям связи.

3. Профильно проецирующая прямая параллельна одновременно П₁ и П₂, следовательно, [M₂N₂] = [M₁N₁] = |MN|.

Дата добавления: 2014-10-23