Геометрические построения в задаче 2 а

Определить натуральную величину отрезка прямой линии и углы наклона к плоскостям проекций способом прямоугольного треугольника.

Пример решения типовых задач

Задача 2 а. Даны точки с координатами – А(70; 30; 15), В(10; 30; 65).

1. По заданным координатам построить проекции отрезка в системе плоскостей П₁П₂.

Алгоритм решения.

1. По данным координатам определить положение прямой линии относительно плоскостей проекций: координаты Y у точек А и В равны, Y_A=Y_B=30, следовательно, точки А и В равноудалены от фронтальной плоскости проекций П₂, отрезок прямой линии АВ параллелен фронтальной плоскости проекций П₂, ABIIП₂. Таким образом, отрезок прямой линии АВ является фронтальной прямой.

2. Выделить свойства проекций прямых, параллельных плоскостям проекций: так как отрезок прямой линии АВ параллелен фронтальной плоскости П₂, ABIIП₂, то согласно свойству проецирования [14] фронтальная проекция отрезка прямой линии А₂В₂ равна натуральной величине АВ, lАВl = А₂В₂ .

3. Построить проекции отрезка прямой линии AB по координатам двух её точек (табл. 4.2).

4. Применить метод прямоугольного треугольника для определения натуральной величины отрезка прямой линии АВ на плоскости П₁ (табл. 4.2).

Таблица 4.2

Словесная форма	Графическая форма
1. Отложить на осях координат x, y, z значение координат для точек А и В. 2. Построить проекции точек A и B:А1(x; –y), В1(x; –y), А2(x; z), В2 (x;z)
3. Соединить одноименные проекции: А1 с В1, А2 с В2. Получим проекции отрезка АВ: [А1В1] и [А2В2]
4. Определить ΔΖ и ΔY отрезка АВ: ΔZ – это разность расстояний удален­ности точек А и В до П1; ΔΖ = Bz – Az = 65 – 15 = 50, ΔY – это разность расстояний удаленности точек А и В от П2, ΔY = By – Ay = 30 – 30 = 0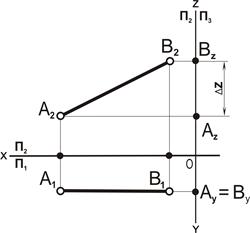

Окончание табл. 4.2

Словесная форма	Графическая форма
5. От точки В1 на перпендикуляре отложить Δz, |В1В`1|= ΔΖ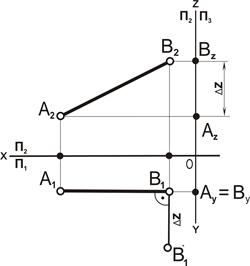
6. Соединить точки А1 с В`1. Отрезки А1 В`1 и А2В2 являются натуральной величиной отрезка АВ, так как (AB)|| П1, lАВl = |А`1 В1 | = |А`2В2|. 7. a – угол наклона отрезка АВ к плоскости П1

Задача 2 б. Даны точки с координатами А(30; –85; 45), В(20; –40; 65).

1. По заданным координатам построить проекции отрезка в системе плоскостей П₁П₂.

Дата добавления: 2014-10-23