Дипольная теория электрокардиограммы

Теория отведений Эйнтховена, три стандартных отведения

Форма и размер зубцов электрокардиограммы зависит от положения электродов на поверхности тела. Существует биполярное и униполярное отведения.

Эйнтховен предложил использовать стандартные биполярные отведения: отведение 1 - между правой и левой руками; отведение II - между правой рукой и левой ногой; отведение III - между левой рукой и левой ногой.

При записи ЭКГ в стандартных отведениях конечности рассматриваются как проводники электрического тока. Следовательно, можно сказать, что потенциалы записываются в точках прикрепления конечностей. Эти точки формируют вершины равностороннего треугольника (треугольникЭйнтховена), стороны которого являются осями соответствующих отведений (рис.6).

Рис. 6. Биполярные отведения ЭКГ, по Эйнтховену.

Для того чтобы получить униполярные отведения, 1 активный электрод устанавливается в некоторой точке поверхности тела. Есть несколько систем униполярных отведений, которые изучаются в деталях в ходе физиологии.

Чтобы понять происхождение электрокардиограммы нужно принять во внимание, что электрическое поле сердца является результатом наложения электрических полей множества сердечных клеток.

Мембранный потенциал покоящейся клетки не вызывает появления потенциала в любой точке тела. Клетка, несущая импульс, может быть поделена на две части: покоящуюся и активную. Покоящаяся часть имеет неизменный мембранный потенциал. Активная часть имеет потенциал, равный величине потенциала действия. Переход между двумя частями происходит в какой-либо точке.

На рис. 8 показана диаграмма осевого сечения клетки с волной деполяризации около центра (A). Электрический потенциал в любой внешней точке такой, какой мог бы быть получен, если бы заряды мембраны располагались в поперечном сечении (Б). Таким образом, каждая из возбужденных сердечных клеток представляет собой диполь, который имеет элементарный дипольный момент определенной величины и направления.

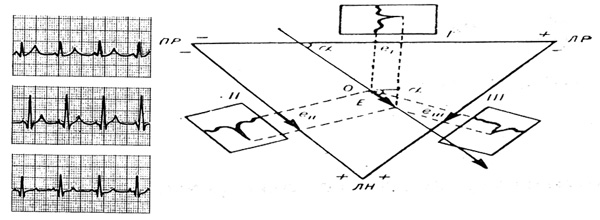
Рис. 7. Треугольник Эйнтховена и ЭКГ, записанные в соответствующих отведениях

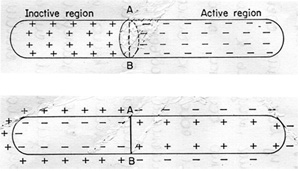Рис. 8. Диаграмма возбужденной сердечной клетки.

В любой момент возбуждения, дипольные моменты отдельных клеток суммируются, формируя суммарный дипольный момент всего сердца. Суммарный дипольный момент сердца является результатом наложения дипольных моментов клеток. Вот почему сердце можно рассматривать как дипольный электрический генератор.

Направление суммарного дипольного момента сердца часто называют электрической осью сердца. Этот дипольный момент определяет величину разности электрических потенциалов, записанную на поверхности тела. Электрический потенциал, измеренный в любой точке, отдалённой от источника, зависит главным образом от величины суммарного дипольного момента сердца и угла между его направлением и осью отведения ЭКГ (Рис. 7).

Одной из значимых проблем в электрокардиографии является определение направления электрической оси сердца. Его определяют, измеряя амплитуду (напряжение) отклонений ЭКГ в стандартных отведениях Эйнтховена. Стандартные отведения дают возможность изучать проекции электрической оси сердца на фронтальную плоскость.

Чтобы определить направление электрической оси сердца необходимо ввести некоторые упрощения:
- пренебречь электрическим сопротивлением конечностей;
- рассматривать треугольник Эйнтховена как равносторонний;
- считать, что сердце расположено в центре равностороннего треугольника.

Амплитуда (напряжение) каждого отклонения ЭКГ равна суммарному дипольному моменту сердца, умноженному на косинус угла между электрической осью сердца и осью соответствующего отведения (3). Эти амплитуды можно также определить как проекции суммарного дипольного момента сердца на соответствующие оси отведений, которые являются сторонами треугольника Эйнтховена.

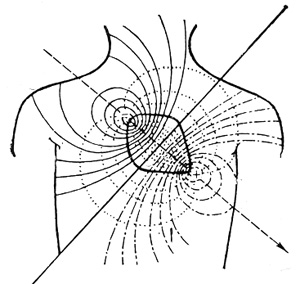Рис. 9. Электрическая ось сердца

Направление электрической оси сердца не является постоянным, но изменяется в каждый момент времени. Его удобно определять для комплекса QRS. Для этого необходимо измерить амплитуду отклонений Q, R и S в I и III стандартных отведениях и вычислить алгебраическую сумму величин положительного и отрицательного отклонений. Полученные разности отложить в произвольном масштабе на соответствующих сторонах треугольника Эйтховена, начиная от центра (в положительном или отрицательном направлении, в зависимости от того, положительна или отрицательна разность). Из полученных таким образом точек на осях отведений опустить перпендикуляры. Точка их пересечения укажет конец вектора электрической оси сердца (начало - в центре треугольника).

Чтобы определить направление электрической оси, необходимо измерить угол между полученным вектором и горизонтальной линией. В норме он составляет от 0 до +90 градусов. Существуют такие варианты направления электрической оси сердца: нормограмма (от 0⁰ до +90⁰): горизонтальное положение (от 0⁰ до 40⁰), нормальное (от 40⁰ до 70⁰)ти вертикальное (от 70⁰ до 90⁰); правограмма (от 90⁰ до 180⁰), левограмма (от 0⁰до - 90⁰).

Дата добавления: 2014-10-23