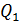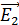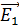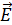КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
План решения задач. С помощью принципа суперпозиции
|
|
|
|
С помощью принципа суперпозиции
Расчет напряженности и потенциала электростатического поля
1.Изобразите на рисунке схему расположения точечных зарядов или заряженных тел в соответствии с условием задачи. На схеме: 1) покажите знаки зарядов и их символы с индексом, равным номеру заряда; 2) обозначьте точку, в которой нужно определить величины напряженности и потенциала ЭСП, например, точка 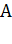 .
.
2. Запишите принцип суперпозиции для расчета напряженности поля в следующем виде:
а) если ЭСП создается системой точечных зарядов или заряженных тел, то результирующий вектор
 (1)
(1)
где 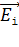 – вектор напряженности поля i-того заряда или заряженного тела; число слагаемых в уравнении (1) равно числу зарядов, создающих поле;
– вектор напряженности поля i-того заряда или заряженного тела; число слагаемых в уравнении (1) равно числу зарядов, создающих поле;
б) если ЭСП создается зарядом, распределенным равномерно, например, по длине заряженного тела, тогда
 , (2)
, (2)
где  – бесконечно малый вектор напряженности, создаваемый элементарным зарядом
– бесконечно малый вектор напряженности, создаваемый элементарным зарядом 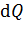 , выделенным на заряженном теле.
, выделенным на заряженном теле.
3. Так как в уравнениях (1) и (2) записана сумма векторов, которые следует складывать геометрически, то необходимо показать на рисунке направления суммируемых векторов. Для этого мысленно помещают в исследуемую точку поля А пробный положительный заряд 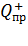 и показывают направление сил
и показывают направление сил 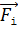 , действующих на этот пробный заряд со стороны каждого i-того заряда (естественно, что векторы всех сил, приложенных к заряду
, действующих на этот пробный заряд со стороны каждого i-того заряда (естественно, что векторы всех сил, приложенных к заряду 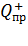 , начинаются в точке А). Поскольку векторы напряженности
, начинаются в точке А). Поскольку векторы напряженности 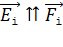 , то обозначают изображенные векторы символами
, то обозначают изображенные векторы символами 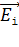 , где индекс величины
, где индекс величины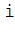 совпадает с индексом заряда, создающего поле. Аналогично определяют направление векторов
совпадает с индексом заряда, создающего поле. Аналогично определяют направление векторов 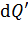 , которые выбирают, как правило, в точках заряженного тела, распложенных симметрично относительно его оси симметрии.
, которые выбирают, как правило, в точках заряженного тела, распложенных симметрично относительно его оси симметрии.
4. Сложение двух векторов 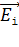 обычно выполняют с помощью правила параллелограмма (или треугольника); при этом модуль определяемого результирующего вектора находят по теореме косинусов. Если число складываемых векторов равно трем и более, в том числе и при суммировании бесконечно малых векторов
обычно выполняют с помощью правила параллелограмма (или треугольника); при этом модуль определяемого результирующего вектора находят по теореме косинусов. Если число складываемых векторов равно трем и более, в том числе и при суммировании бесконечно малых векторов 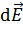 , то находят проекции результирующего вектора
, то находят проекции результирующего вектора 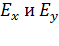 на координатные оси
на координатные оси 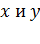 , проецируя на эти оси каждый из суммируемых векторов. В этом случае модуль результирующего вектора определяют с помощью теоремы Пифагора:
, проецируя на эти оси каждый из суммируемых векторов. В этом случае модуль результирующего вектора определяют с помощью теоремы Пифагора: 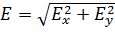 . Оси направляют таким образом, чтобы удобно было записывать проекции
. Оси направляют таким образом, чтобы удобно было записывать проекции 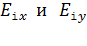 , т. е. чтобы были известны углы, образованные векторами
, т. е. чтобы были известны углы, образованные векторами 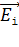 с осями координат. Либо одну из осей проводят по предполагаемому направлению результирующего вектора
с осями координат. Либо одну из осей проводят по предполагаемому направлению результирующего вектора 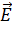 , которое можно определить, используя симметрию в расположении зарядов, если таковая имеется.
, которое можно определить, используя симметрию в расположении зарядов, если таковая имеется.
5. Потенциал электростатического поля в исследуемой точке А находят также с помощью принципа суперпозиции:
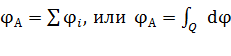 , (3)
, (3)
алгебраически суммируя потенциалы, которые создаются в данной точке А заряженными телами, в том числе, точечными зарядами  или бесконечно малыми точечными зарядами
или бесконечно малыми точечными зарядами 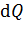 . При этом суммировании знаки потенциалов
. При этом суммировании знаки потенциалов 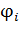 равны знакам соответствующих
равны знакам соответствующих  -тых зарядов, в частности, отрицательный заряд создает в точке А электростатическое поле с отрицательным значением потенциала.
-тых зарядов, в частности, отрицательный заряд создает в точке А электростатическое поле с отрицательным значением потенциала.
Задача 4. Два точечных заряда 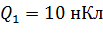 и
и 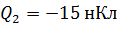 расположены в двух вершинах равностороннего треугольника со стороной
расположены в двух вершинах равностороннего треугольника со стороной  . Определите напряженность
. Определите напряженность 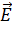 электростатического поля и его потенциал в точке А, находящейся в третьей вершине.
электростатического поля и его потенциал в точке А, находящейся в третьей вершине.
|
|
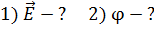
|
 Рис. 11 |
Расположение зарядов 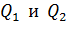 относительно точки А показано на рис. 11.
относительно точки А показано на рис. 11.
1) Для расчета напряженности 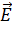 используем принцип суперпозиции ЭСП в виде:
используем принцип суперпозиции ЭСП в виде:
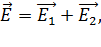 (1)
(1)
где 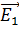 и
и 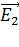 – напряженности полей, создаваемых в точке А зарядами
– напряженности полей, создаваемых в точке А зарядами  соответственно.
соответственно.
Чтобы определить направление складываемых векторов, в точку А мысленно помещаем пробный заряд 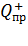 и рассматриваем действующие на него силы: первый заряд
и рассматриваем действующие на него силы: первый заряд 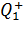 отталкивает заряд
отталкивает заряд 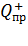 силой
силой 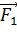 , направленной по линии соединяющей заряды
, направленной по линии соединяющей заряды 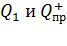 , а второй – отрицательный заряд
, а второй – отрицательный заряд  притягивает к себе положительный заряд
притягивает к себе положительный заряд 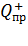 силой
силой 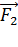 , также направленной по линии, соединяющей заряды
, также направленной по линии, соединяющей заряды  . Напряженность поля, создаваемого i-тым зарядом,
. Напряженность поля, создаваемого i-тым зарядом, 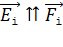 , т. Е. совпадает по направлению с соответствующей силой.
, т. Е. совпадает по направлению с соответствующей силой.
Модуль результирующего вектора  можно найти любым из двух способов: а) по теореме косинусов:
можно найти любым из двух способов: а) по теореме косинусов:
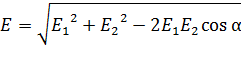 , (2)
, (2)
где напряженности ЭСП, создаваемого точечными зарядами  в точке А, находящейся на расстоянии
в точке А, находящейся на расстоянии  от каждого заряда:
от каждого заряда:
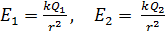 ; (3)
; (3)
б) по проекциям принципа суперпозиции (1) на координатные оси 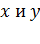 :
:
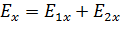 ; (4)
; (4)
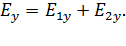 (5)
(5)
Ось 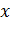 направляем вдоль вектора
направляем вдоль вектора 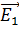 , при этом вектор
, при этом вектор 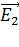 образует известные углы
образует известные углы  с осями
с осями 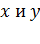 (см. рис. 11). Следовательно, проекции результирующего вектора
(см. рис. 11). Следовательно, проекции результирующего вектора  :
: 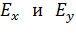 , – на координатные оси
, – на координатные оси 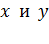 , будут определяться выражениями:
, будут определяться выражениями:


В результате
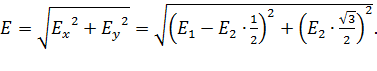 (6)
(6)
Подставим формулы (3) для напряженностей 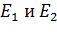 в выражение (6) и, вынося одинаковый сомножитель
в выражение (6) и, вынося одинаковый сомножитель  за скобки и из радикала, получим следующую расчетную формулу величины
за скобки и из радикала, получим следующую расчетную формулу величины  :
:
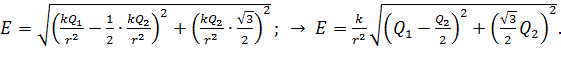 (7)
(7)
Вычисляем по формуле (7) напряженность электростатического поля в точке А, заметив, что при этом нужно подставлять модуль отрицательного заряда 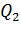 , поскольку знак его уже учтен в направлении вектора
, поскольку знак его уже учтен в направлении вектора 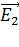 :
:
 .
.
2) Расчет потенциала  в точке А электростатического поля выполняем, используя принцип суперпозиции:
в точке А электростатического поля выполняем, используя принцип суперпозиции:
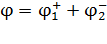 , (8)
, (8)
где потенциалы ЭСП, созданного точечными зарядами  в точке А, находящейся на расстоянии
в точке А, находящейся на расстоянии  от каждого заряда, определяются следующими формулами:
от каждого заряда, определяются следующими формулами:
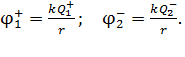 (9)
(9)
С учетом этих формул равенство (8) запишется в виде:
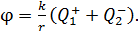 (10)
(10)
В полученной расчетной формуле каждый заряд записывается с его знаком, так как только в этом случае получим алгебраическую сумму потенциалов полей, создаваемых отдельными зарядами. Вычислим потенциал в исследуемой точке электростатического поля по формуле (10):
 .
.
Задача 5. Четыре точечных заряда 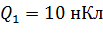 ,
, 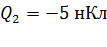 ,
, 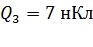 и
и 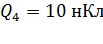 , расположены в вершинах квадрата со стороной
, расположены в вершинах квадрата со стороной 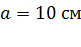 . Определите напряженность
. Определите напряженность 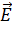 ЭСП и его потенциал
ЭСП и его потенциал  в точке О пересечения диагоналей квадрата.
в точке О пересечения диагоналей квадрата.
|
|
|
|
|
Дата добавления: 2014-10-23; Просмотров: 1231; Нарушение авторских прав?; Мы поможем в написании вашей работы!

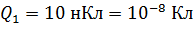 ;
;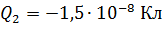 ;
; ;
;