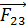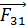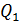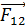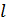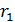КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дано Решение
|
|
|
|
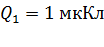 ; ;
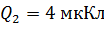 ; ;
 . .
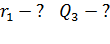
|

Рис. 8 |
Покажем на рис. 8 силы  и
и 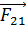 взаимного отталкивания зарядов
взаимного отталкивания зарядов  и
и 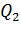 . Чтобы заряды
. Чтобы заряды  и
и 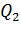 были в равновесии, нужно скомпенсировать эти силы противоположно им направленными силами
были в равновесии, нужно скомпенсировать эти силы противоположно им направленными силами  – на первый заряд и
– на первый заряд и  – на второй. Такие силы создает отрицательный заряд
– на второй. Такие силы создает отрицательный заряд 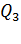 , помещенный между зарядами
, помещенный между зарядами  и
и 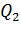 . На этот заряд
. На этот заряд 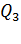 будут действовать силы
будут действовать силы  и
и 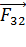 со стороны первого и второго зарядов соответственно.
со стороны первого и второго зарядов соответственно.
Запишем условия равновесия зарядов:  , – для каждого заряда.
, – для каждого заряда.
Для  :
:  ; (1)
; (1)
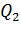 :
: 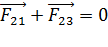 ; (2)
; (2)
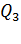 :
: 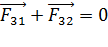 . (3)
. (3)
Отметим, что силы взаимодействия зарядов удовлетворяют третьему закону Ньютона:
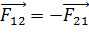 ;
; 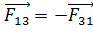 ;
;  ; (4)
; (4)
С учетом равенства модулей сил, входящих в третий закон Ньютона, и условий равновесия зарядов (1), (2) и (3) получаем, что модули всех сил парного взаимодействия зарядов одинаковы. Это очевидно и по рис. 8.
Обозначим расстояния:  – заряда
– заряда 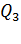 от
от  ;
;  – заряда
– заряда 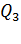 от
от 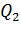 , при этом
, при этом  , – и запишем модули сил, используя закон Кулона:
, – и запишем модули сил, используя закон Кулона:
 ; (5)
; (5)
 ; (6)
; (6)
 ; (7)
; (7)
Приравниваем формулы сил (5) и (6) в соответствии с условием (3) равновесия заряда 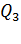 :
:
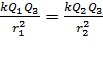 , после сокращения получаем
, после сокращения получаем 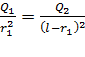 . (8)
. (8)
Решаем уравнение (8) с одной неизвестной величиной  , извлекая из обеих частей равенства квадратный корень:
, извлекая из обеих частей равенства квадратный корень:
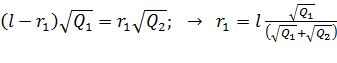 .(9)
.(9)
Вычисляем 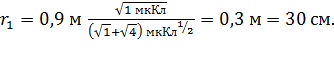 Таким образом, заряд
Таким образом, заряд 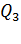 следует поместить на расстоянии
следует поместить на расстоянии  от заряда
от заряда  .
.
Величину заряда 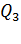 найдем, приравнивая модули сил
найдем, приравнивая модули сил 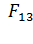 и
и 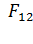 , согласно условию (1) равновесия заряда
, согласно условию (1) равновесия заряда  :
:
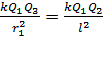 , после сокращения имеем
, после сокращения имеем  .
.
Вычислим величину заряда 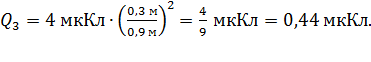
Задача 2. Два шарика одинаковых радиуса 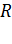 и массы
и массы 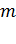 подвешены на нитях одинаковой длины
подвешены на нитях одинаковой длины  так, что они соприкасаются. После сообщения шарикам заряда
так, что они соприкасаются. После сообщения шарикам заряда  каждому, они оттолкнулись друг от друга, а нити образовали угол
каждому, они оттолкнулись друг от друга, а нити образовали угол 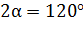 . Найдите массу шарика и силу натяжения нити. Примите, что
. Найдите массу шарика и силу натяжения нити. Примите, что 
|
|
|
|
|
Дата добавления: 2014-10-23; Просмотров: 454; Нарушение авторских прав?; Мы поможем в написании вашей работы!