Верифікація моделі

Показники якості моделі

В емпіричних економічних і соціальних дослідженнях не завжди відомо, скільки факторів має бути введено в модель і яка форма залежності краще описує реальні зв'язки. Щоб забезпечити найбільш адекватне відтворення досліджуваного явища чи процесу, необхідно вибрати регресійну функцію середбагатьох варіантів, використовуючи спеціальні критерії якості моделі.

Для перевірки коректності побудови моделі визначають насамперед:

- стандартну похибку рівняння;

- коефіцієнт детермінації;

- коефіцієнтмножинної кореляції;

- стандартну похибку параметрів.

Зазначені показники отримують на підставі конкретних статистичних даних, тобто кожна з цих характеристик є вибірковою характеристикою і тому має бути перевірена на значущість за допомогою спеціальних статистичних критеріїв.

Стандартна похибка рівняння (точкова оцінка емпіричної дисперсії залишків) характеризує абсолютну величину розкиду випадкової складової рівняння і обчислюється за формулою

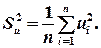
Зрозуміло, що перевага віддається моделям, у яких стандартна похибка рівняння менша порівняно з іншими моделями.

Коефіцієнт детермінації 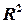показує, яка частина руху (варіації) залежної змінної описується даним регресійним рівнянням, і обчислюється за формулою

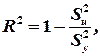
де

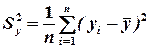– емпірична дисперсія незалежної змінної;

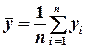– середнє значення залежної змінної.

На значення коефіцієнта детермінації виливає кількість факторів, що враховано в моделі. Уведення в модель кожної нової змінної збільшує значення коефіцієнта детермінації. Тому щоб запобігти не­виправданому розширенню моделі й мати змогу порівнювати моделі з різною кількістю факторів, уводять спеціальний оцінений ко­ефіцієнт детермінації, який враховує число параметрів моделі, число ступенів свободи:

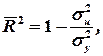
де

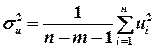– незміщена оцінка дисперсії залишків;

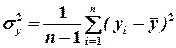– незміщена оцінка дисперсії залежної змінної.

Неважко помітити, що обидва коефіцієнти пов'язані такою залеж­ністю:

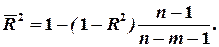
Обчислений у такий спосіб коефіцієнт детермінації називається скоригованим за Тейлом.

Зауваження. Коефіцієнт детермінації має ще хоча б одне рівноцінне оз­начення. Зокрема, він дорівнює квадрату емпіричного коефіцієнта кореляції між двома рядами спостережень: емпіричними значеннями залежної змінної 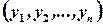та його розрахунковими (теоретичними) значеннями і обчислюється за формулою

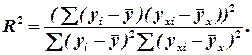
Коефіцієнт множинної кореляції 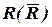визначає міру зв'язку за­лежної змінної з усіма незалежними факторами і є коренем квадрат­ним з відповідного коефіцієнта детермінації: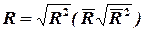

Стандартні похибки оцінок параметрів моделі обчислюються за формулою:

,

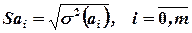де

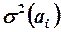– діагональні елементи матриці коваріацій оцінок параметрів моделі (коваріаційної матриці).

Коваріаційна матриця:

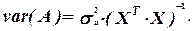
Стандартні похибки оцінок параметрів моделі порівнюються з самими оцінками шляхом обчислення відношень:

.

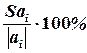Якщо таке відношення перевищує 50%, то відповідна оцінка параметру моделі може мати зміщення.

Стандартна похибка рівняння, коефіцієнт детермінації та множин­ної кореляції є характеристиками, за якими перевіряється пра­вильність вибору незалежних змінних моделі. При порівнянні регресійних рівнянь з різною кількістю незалежних змінних вирішальними критеріями є стандартна похибка рівняння (найменша) та коефіцієнт детермінації (якомога ближчий до одиниці і з більшим числом сту­пенів свободи).

Перевірка значущості та довірчі інтервали

Розглянуті показники якості моделі побудовані за даними спостережень, тобто є деякими вибірковими характеристиками генеральної сукупності. З математичної статистики відомо, що будь-яка статистика (функція від елементів вибірки) має бути перевірена на значущість. Іншими словами, за допомогою спеціальних критеріїв не­обхідно встановити, чи зумовлено значення цієї функції лише похибками вимірювання, чи вона відображає якусь суттєву (значущу) інформацію. Неперевірений статистичний результат є лише деякою гіпотезою, яка може бути прийнята чи відхилена.

Стосовно кожного статистичного результату висувається так зва­на нульова гіпотеза (про рівність нулю деякої випадкової величини) і альтернативна до неї гіпотеза (про її суттєву відмінність від нуля). У нульовій гіпотезі формулюють результат, який бажано відхилити, а в альтернативній, яка інакше називається експериментальною, – той, що його необхідно підтвердити.

Рівність двох величин у загальному випадку може розглядатися як рівність нулю їх різниці.

За заданим рівнем значущості множина допустимих значень роз­бивається на дві неперетинні множини: одна містить значення випад­кової величини, ймовірність досягнення яких перевищує заданий рівень значущості, а інша – критична область – визначає ті значен­ня, що досягаються рідко (імовірність потрапити до такої області нижча від заданого рівня), і розташована вона, як правило, на «хвос­тах розподілу».

Залежно від альтернативної гіпотези критична область може склада­тися з одного чи двох проміжків на числовій осі. Це буде один проміжок(правий чи лівий «хвіст» розподілу), якщо зазначається напрямок нерівності (більше або менше деякої величини), і два проміжки (обидва «хвости» розподілу), якщо встановлюється нерівність (не дорівнює певній величині).

За даними спостережень обчислюється значення відповідної статистики – функції від елементів вибірки. Якщо ця величина потрапляє до критичної області, це означає, що сталася практично неможлива подія, тобто подія, що має дуже малу ймовірність, а отже, від нульової гіпотези слід відмовитися і віддати перевагу альтернативній. Якщо обчислене значення статистики не потрапило до критичної області, роблять висновок, що дана вибірка не суперечить нульовій гіпотезі, тобто неправильною є експериментальна гіпотеза.

При перевірці гіпотез може бути допущена помилка, наприклад може бути відхилена нульова гіпотеза, хоча насправді вона правильна (помилка першого роду), або ж, навпаки, нульова гіпотеза може бути прийнята, хоча вона неправильна (помилка другого роду). На це слід зважати при формулюванні статистичного висновку.

Якщо значення 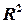«близьке» до одиниці, вважається, що регресійне рівняння досить правильно відбиває наявний зв'язок між залежною та незалежними змінними моделі. Якщо значення 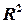«близьке» до нуля – регресійна модель неправильна. Постає питання, як визначити цю «близькість»? Для цього необхідно застосувати відповідний статистиці ний критерій, який дасть змогу встановити, чи суттєво відрізняється 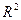від нуля, чи ця відмінність пов'язана з особливостями конкретних даних, тобто зумовлена лише похибками вимірювань.

Для перевірки статистичної значущості коефіцієнта детермінації 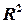висувається нульова гіпотеза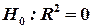. Це означає, що досліджуване рівняння не пояснює змінювання регресанта (результативного показника) під впливом відповідних регресорів (факторних показників). У такому разі всі коефіцієнти при незалежних змінних мають дорівнювати нулю. При цьому нульову гіпотезу можна подати у вигляді

Альтернативною до неї є Н_А: значення хоча б одного параметра моделі відмінне від нуля, тобто хоча б один із факторів впливає на змінювання залежної змінної.

Для перевірки цих гіпотез застосовують 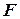-критерій Фішера з і 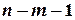ступенями свободи. За отриманими в моделі значеннями коефіцієнта детермінації 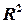обчислюють експериментальне значен­ня 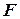-статистики:

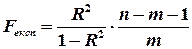
яке порівнюють з табличним значенням 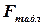розподілу Фішера при зада­ному рівні значущості 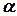(як правил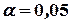о, або 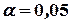). Якщо , тоді нульова гіпотеза відхиляється, тобто існує такий коефіцієнт у регресійному рівнянні, який суттєво відрізняється від нуля, а відповідний фактор впливає на досліджувану змінну. Відхи­лення нуль-гіпотези свідчить про адекватність побудованої моделі. У протилежному випадку модель вважається неадекватною.

Коефіцієнт кореляції, як вибіркова характеристика, перевіряєть­ся на значущість за допомогою t -критерію Стьюдента. Фактичне зна­чення t -статистики обчислюється за формулою

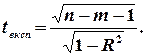
і порівнюється з табличним значенням t -розподілу з 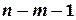ступе­нями свободи та при заданому рівні значущості 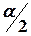(такий рівень зу­мовлений тим, що критична область складається з двох проміжків). Якщо абсолютна величина експериментального значення t -статисти­ки перевищує табличне, тобто

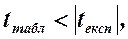
то можна зробити висновок, що коефіцієнт кореляції достовірний (зна­чущий), а зв'язок між залежною змінною та всіма незалежними фак­торами суттєвий.

Окрім загальних показників адекватності моделі існують також оцінки, що дають змогу встановити якість окремих частин рівняння, зокрема одного чи кількох коефіцієнтів регресії. Як і в попередніх випадках, рішення відносно якості коефіцієнтів приймають на основі відповідних статистичних критеріїв.

Статистичну значущість кожного параметра моделі можна перевірити за допомогою t -критерію. При цьому нульова гіпотеза має вигляд альтернативна

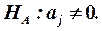
Експериментальне значення t -статистики для кожного параметра моделі обчислюється за формулою

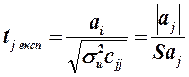
де 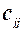– діагональний елемент матриці помилок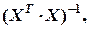 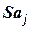– стандартна похибка оцінки параметра моделі, .

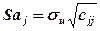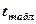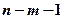Експериментальне значення t -критерію порівнюється з таблич­ним значенням з ступенями свободи при заданому рівні значущості 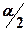. Якщо значення t -статисти­ки потрапляє до критичної області (за абсолютним значенням пере­вищує 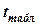), приймається альтернативна гіпотеза про значущість відповідного параметра. Інакше робиться висновок про статистичну незначущість параметра 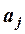, а це означає, що відповідна незалежна змінна не виливає суттєво на змінювання регресанта.

Зауваження. Оскільки t -статистика є відношенням відповідного параметра моделі до його стандартної похибки (середньоквадратичного відхилення), то на практиці частіше застосовують грубішу оцінку, а саме допускають, щоб стандартні похибки становили 45-50% значен­ня параметра, аби стверджувати про його статистичну значущість.

Довірчі інтервали для кожного окремого параметра 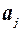обчислюються на основі його стандартної похибки та критерію Стьюдента:

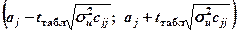
Табличне значення 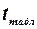, як і раніше, має 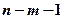ступенів сво­боди і рівень значущості :

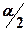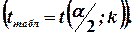
Дата добавления: 2014-10-23