Поняття ідентифікації (ототожнення) системи рівнянь

Маючи дві форми системи одночасних рівнянь, необхідно визна­чити, яка з них краще підходить для оцінювання параметрів моделі. Передусім необхідно дослідити можливості застосування звичайного МНК до окремих рівнянь системи.

Як зазначалося раніше, для отримання незміщених і обґрунтованих оцінок параметрів регресійного рівняння за звичайним МНК необхідно виконати ряд передумов: залишки моделі мають бути ви­падковими величинами з нульовим математичним сподіванням, зі сталими дисперсіями, некорельованими між собою та незалежними відносно ендогенних змінних моделі.

Щоб забезпечити необхідну якість оцінок параметрів (незміщеність, ефективністьі обґрунтованість), потрібно спробувати на підставі оцінених па­раметрів скороченої (зведеної) форми системи рівнянь отримати оцін­ки параметрів структурної форми. Однак тут виникає проблема одно­значних залежностей між параметрами: при поверненні від скороченої форми моделі до структурної (обернені перетворення) можна отрима­ти єдине значення шуканого параметра чи кілька різних значень або взагалі не мати змоги отримати жодного.

Щоб передбачити можливі варіанти розв'язання задачі оцінювання параметрів системи одночасних рівнянь, необхідно попередньо досліди­ти модель, а саме перевірити ідентифікованість системи. Під проблемою ідентифікації розуміють можливість чисельної оцінки параметрів струк­турних рівнянь за оцінками коефіцієнтів зведених рівнянь.

Означення 8.4. Економетрична модель, задана системою одночас­них рівнянь, називається точно (строго) ідентифікованою (ототож­неною), якщо однозначно можна отримати оцінки її параметрів па основі оцінених параметрів зведеної моделі.

Означення 8.5. Надідентифікованою (переототожненою) нази­вається така модель, що для деяких її параметрів можна отримати кілька кількісних значень па підставі параметрів зведеної форми.

Крім того, модель може бути неідентифікованою (неототожненою). Це трапляється в тому разі, якщо кількість невідомих пара­метрів набагато перевищує кількість рівнянь, через які їх треба оці­нити.

Отже, перехід від структурної до зведеної форми системи рівнянь хоча й дає змогу усунути проблему корельованості пояснюючої змінної та випадкового відхилення, однак призводить до іншої не менш серйозної проблеми — проблеми ідентифікованості.

Щоб зрозуміти проблему ідентифікованості, необхідно усвідоми­ти суть принципових розбіжностей між структурними та зведеними рівняннями.

Необхідні й достатні умови ідентифікованості

Щоб швидше формально визначити ідентифікованість структур­них рівнянь, застосовують такі необхідні й достатні умови. Нехай система одночасних рівнянь містить рівнянь відносно ендоген­них змінних, а також 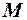екзогенних або заздалегідь визначених змінних. Крім того, для деякого рівняння кількість ендогенних і ек­зогенних змінних у перевірці на ідентифікованість дорівнює відпо­відно 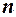і 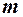. 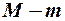Змінні, що не входять у дане рівняння, але входять в інші рівняння системи, назвемо виключеними змінними (з даного рівнян­ня), їх кількість дорівнює для ендогенних і для екзогенних змінних.

Перша необхідна умова. Рівняння ідентифіковане, якщо воно вик­лючає принаймні 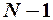змінну (ендогенну чи екзогенну), що присут­ня в моделі:

.

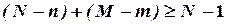Друга необхідна умова. Рівняння ідентифіковане, якщо кількість виключених з нього екзогенних змінних не менше кількості ендоген­них змінних у цьому рівнянні, зменшеної на одиницю: .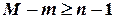

Знаки рівності в обох необхідних умовах відповідають точній іден­тифікованості рівняння.

Наведемо приклади використання зазначених умов для визначен­ня ідентифікованості структурних рівнянь.

1. У простій моделі «попит — пропозиція»

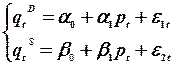
маємо:

Для кожного з рівнянь 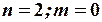. Отже, перша не­обхідна умова не виконується для обох рівнянь, тому що

.

Це означає, що вони обидва неідентифіковані.

2. Додамо до функції попиту екзогенну змінну (прибуток споживачів):

маємо: 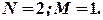Для кожного з рівнянь 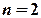. Для першого рівняння , для другого 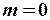. Тоді для першого рівняння . А це означає, що перша необхідна умова не виконується і дане рівняння неідентифіковане. Для друго­го рівняння цієї системи 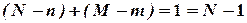,тобто дане рівняння точно ідентифіковане. Отже, функція пропозиції може бути визначена однозначно.

3. У моделі:

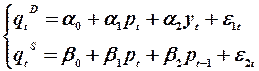
. Для кожного рівняння системи , 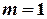. Для кожного з рівнянь виконується умова:

.

Отже, обидва рівняння системи є точно ідентифікованими.

4. У моделі «попит — пропозиція», де враховано три екзогенні змінні:

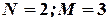. Для кожного рівняння системи . Кількість вик­лючених змінних у першому рівнянні . Тоді перше рівняння точно ідентифіковане, тому що для нього .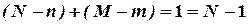

Для другого рівняння 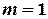. Отже, для нього

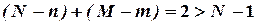. Це рівняння є перевизначеним.

Для однозначної оцінки коефіцієнтів функції пропозиції в цьому разі необхідно використовувати інші спеціальні методи оцінювання пара­метрів.

Дата добавления: 2014-10-23