Маса системи. Центр мас

Рух системи залежить від її маси і від розподілу мас у системі.

Маса системи (позначається М або т) дорівнює арифметичній сумі мас всіх точок або тіл, що утворюють цю систему:

Розподіл мас у системі визначається значенням мас т_k і їх взаємним положенням, тобто координатами x_k, y_k, z_k. Не завжди при розв’язанні задач динаміки необхідні всі ці величини, потрібні тільки деякі, які виражаються через сумарні характеристики, а саме: координати центра мас, осьові моменти інерції. Ці характеристики ми розглянемо нижче.

Центр мас. Для визначення координат центра мас тіла дещо перетворимо відомі нам формули для визначення центра ваги тіла (див. лекц. №4), таким чином, щоб маса входила в явному вигляді. Для цього врахуємо, що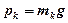, 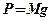(g – прискорення вільного падіння), тоді:

, , .

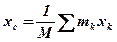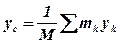Геометрична точка С, координати якої визначаються за цими формулами, називаються центром мас або центром інерції механічної системи.

Якщо положення центра мас визначається його радіусом-вектором 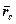, то маємо:

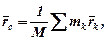
де 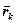– радіуси-вектори точок, які утворюють систему.

Звідси виходить, що для твердого тіла, яке знаходиться в однорідному полі тяжіння (g=const), положення центра мас і центра ваги збігаються.

3. Момент інерції тіла відносно осі. Радіус інерції

Моментом інерції тіла (системи) відносно даної осі Oz (або осьовим моментом інерції) називається скалярна величина, яка дорівнює сумі добутків мас всіх точок тіла (системи) на квадрати їх відстаней від цієї осі:

Звідси виходить, що момент інерції тіла (системи) відносно будь-якої осі є величиною додатною і відмінною від нуля. Одиницею вимірювання моменту інерції в системі СІ є 1 кг ּ м².

Момент інерції є мірою інертності тіла в обертальному русі, так само, як маса в поступальному.

При обчисленні осьових моментів інерції можна виражати відстані точок від осей через координати x_k, y_k, z_k цих точок (так, квадрат відстані від осі Ох буде 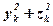і т.д.). Тоді моменти інерції відносно осей Oxyz будуть визначатися формулами:

,

,

.

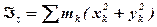Часто при розв’язанні задач доводиться користуватись поняттям радіуса інерції.

Радіусом інерції тіла відносно осі Oz називається лінійна величина ρ_z, яка визначається рівністю:

де M – маса тіла. Із означення виходить, що радіус інерції геометрично дорівнює відстані від осі Oz тієї точки, в якій необхідно зосередити масу всього тіла, щоб момент інерції цієї однієї точки дорівнював моменту інерції всього тіла.

Всі ці формули справедливі як для твердого тіла, так і для будь-якої системи матеріальних точок. У випадку суцільного тіла, розбиваючи його на елементарні частини, знайдемо, що гранично сума в рівності 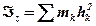перетвориться в інтеграл. У результаті, враховуючи, що 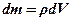, де 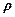– густина, 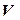– об’єм, маємо:

або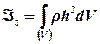

або, враховуючи значення h², дістанемо:

і т.д..

Цими формулами зручно користуватись при обчисленні моментів інерції однорідних тіл правильної форми.

Наведемо формули для осьових моментів інерції деяких простих однорідних тіл.

1. 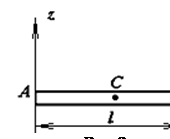Тонкий однорідний стержень довжиною l (рис.2).

Момент інерції відносно осі Az, перпендикулярної стержню, яка проходить через його кінець A:

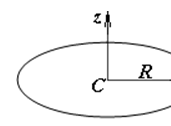
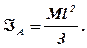
2.Тонке кругле однорідне кільце (рис.3).

.

3. 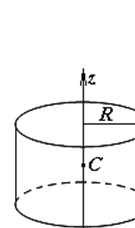Кругла однорідна платівка (рис.3) або циліндр радіусом R (рис.4).

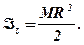
4.Однорідна куля (вісь z напрямлена вздовж діаметра).

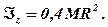
5.Конус масою M з радіусом основи R (вісь z напрямлена вздовж осі конуса).

4. Момент інерції тіла відносно паралельних осей

Встановимо зв’язок між моментами інерції відносно паралельних осей, одна з яких проходить через центр мас системи. Вісь, яка проходить через центр мас тіла, називається центральною.

Оберемо початок прямокутної декартової системи координат в точці C – центрі мас системи (рис.2). У площині yCz проведемо вісь O'z', паралельну Cz і розміщенy на відстані d від неї. Позначимо: h_k– відстань k- ї матеріальної точки від осі z, h'_k– відстань цієї точки від осі z'.

Згідно означення:

Оскільки 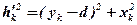, тоді:

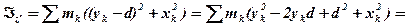
Але 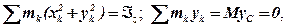оскільки .

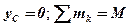Тоді маємо:

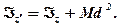
Рис.2

Момент інерції тіла відносно якої-небудь осі дорівнює її моменту інерції відносно центральної осі z, паралельної даній осі z', додатому до добутку маси системи на квадрат відстані між осями.

Із цієї рівності видно, що момент інерції відносно центральної осі найменший у порівнянні з усіма моментами інерції відносно паралельних їй осей.

Питання для самоконтролю

1.Що називається механічною системою?

2.Як класифікуються всі сили, що діють на систему? Їх означення.

3.Викласти властивості внутрішніх сил.

4.Як визначається маса системи, її центр мас?

5.Дати означення моменту інерції тіла відносно осі, навести формули його визначення через координати точок тіла.

6.Що називається радіусом інерції?

7.Як визначаються моменти інерції однорідних тіл: тонкого стержня, тонкого круглого кільця, круглої платівки або циліндра радіусом R, кулі, конуса?

8.Довести, як визначається момент інерції тіла відносно паралельних осей.

Лекція №30

Тема: “Теореми про зміну кількості руху точки та системи і теореми про зміну моменту кількості руху точки та системи”

Дата добавления: 2014-10-23