Маса системи. Центр мас

План

План

План

План

План

План

План

План

План

1..Кінематичний аналіз механізмів методом кінематичних діаграм.

2..Основи аналітичного методу кінематичного дослідження механізмів.

3. Завдання кінематичного синтезу плоских механізмів.

4. Умова існування кривошипа в чотириланкових механізмах.

1. Кінематичний аналіз механізмів методом кінематичних діаграм

Кінематичною діаграмою називається графічне зображення функціональної залежності між двома якими-небудь кінематичними параметрами.

На відміну від методу планів метод кінематичних діаграм дає уявлення про закон зміни відстані, швидкості й прискорення веденої ланки в залежності від кута повороту ведучої.

Цей метод дозволяє побудувати всі кінематичні діаграми по одній із них і тим самим провести повне кінематичне дослідження руху ланки, для якої побудована діаграма.

Першу діаграму можна дістати експериментально. Простіше всього побудувати діаграму переміщення в залежності від часу або кута повороту ведучої ланки.

Розглянемо метод кінематичних діаграм на прикладі. дослідження кривошипно-повзункового механізму (рис.1). Спочатку слід побудувати дванадцять його положень.

У процесі побудови знаходимо методом засічок положення точки В для 12 положень кривошипа (див. лекц.№19).

Визначивши переміщення повзуна, будуємо в довільних масштабах μ_φ і μ_s діаграму переміщень залежно від кута повороту кривошипа (рис.2).

Відрізок 1–1 дістаємо діленням дійсного переміщення повзуна із нульового положення в перше на масштаб переміщення, відрізок 2–2 – із нульового в друге і т.д. Масштаб побудови обчислюємо за формулами:

,; ,; ,.

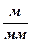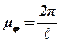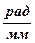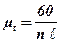Рис.1

Для того щоб дістати закони зміни швидкості й прискорення повзуна від кута повороту кривошипа використовується графічне диференціювання.

Існують такі методи графічного диференціювання:

1) дотичних;

2) хорд.

1. Метод дотичних

Відомо, що швидкість будь-якої точки дорівнює першій похідній від відстані за часом:

або .

Для побудови діаграми швидкостей методом дотичних у точках 1, 2, 3, … до кривої s=f(t) проводимо дотичні.

Нижче креслимо координатні осі v – φ. Вліво від початку координат на продовженні осі абсцис обираємо за полюс точку Р₁ на довільній відстані Н₁, і через неї проводимо паралельно дотичним промені Р₁1¢, Р₁2¢, Р₁3¢,... до перетину з віссю ординат. Перетин горизонтальної прямої 1¢1¢ з серединою інтервалу дасть середнє значення швидкості на даному інтервалі в масштабі:

.

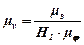Рис.2

Замірявши на діаграмі швидкостей ординати в кожному положенні й помноживши їх на масштаб μ_v, дістанемо дійсні значення швидкостей повзуна у всіх положеннях механізму.

Для побудови діаграми прискорення скористаємось залежністю:

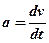або .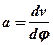

На основі цієї залежності прискорення можуть бути отримані графічним диференціюванням кривої .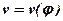

Побудова ведеться аналогічно. Масштаб обчислюється за формулою:

.

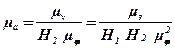Дійсні значення прискорень повзуна в кожному положенні механізму визначаємо, перемноживши ординати на діаграмі а=а(φ) на масштаб побудови μ_а.

2. Метод хорд

Методом хорд виконуються дві дії:

1) графічне диференціювання;

2) графічне інтегрування.

Графічне інтегрування методом хорд є дія, обернена графічному диференціюванню. Метод графічного інтегрування дозволяє за відомим законом зміни прискорення веденої ланки побудувати залежності швидкості й переміщення від кута повороту кривошипа.

Графічне диференціювання методом хорд проводиться аналогічно диференціюванню методом дотичних. Різниця полягає лише в тому, що всі дотичні заміняються хордами.

Те, що таку заміну можна здійснити, випливає із міркувань, відомих із математичного аналізу.

Візьмемо якусь криву MN (рис.3). Оберемо на ній дві довільні точки А і В, сполучивши їх прямою, дістанемо хорду АВ.

Якщо цю січну переміщати, залишаючи паралельною самій собі, то нарешті вона займе положення дотичної Т–Т, причому точка дотикання С буде лежати на кривій між точками А і В. Із зменшенням відстані між точками А і В точка дотикання С буде наближатися до середини дуги АВ. Якщо відстань між точками А і В зробити нескінченно малою, то точка дотику С буде знаходитись на відстані, нескінченно малій від середини дуги АВ.

Графічне диференціювання методом хорд виконується таким чином.

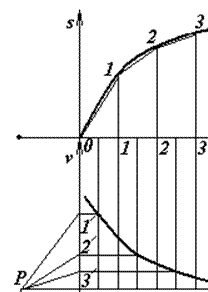Розділимо вісь абсцис діаграми s=s(φ) на інтервали 0–1, 1–2, 2–3 і т. д. Провівши ординати кривої s=s(φ),дістанемо точки ділення на діаграмі 1, 2, 3, .... Сполучивши їх, отримаємо хорди 0–1, 1–2, 2–3, ….

Обираємо нові осі координат для побудови діаграми .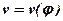

Розділимо вісь абсцис на такі ж інтервали і оберемо вліво від початку координат по осі абсцис полюс Р на довільній довжині Н. Через полюс Р проведемо промені, паралельні хордам. Відрізки на осі ординат, що відтинаються цими променями, є середніми швидкостями на відповідних інтервалах.

Ординату швидкостей, яка відтинається променем Р–1¢, переносимо на середину інтервалу 0–1, ординату швидкості, що відтинається променем Р–2¢ – на середину інтервалу 1–2 і т.д. Сполучимо отримані точки плавною кривою. Маємо діаграму залежності v=v(φ) у масштабі:

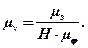
Аналогічно будується залежність а=а(φ).

2..Основи аналітичного методу кінематичного дослідження механізмів

Вище розглянуті графічні методи наочні й універсальні, тому що дозволяють визначати положення, швидкості та прискорення ланок механізмів будь-якої структури. Але графічні методи не завжди мають таку точність, яка буває необхідною в деяких конкретних задачах аналізу механізмів. У цих випадках перевагу віддають аналітичним методам, за допомогою яких дослідження кінематики механізмів може бути виконано з будь-якою точністю. Крім того, аналітичні залежності дозволяють виявити взаємозв’язок кінематичних параметрів механізму з його метричними параметрами, тобто розмірами ланок.

Роль аналітичного методу за останні роки дуже зросла у зв’язку з тим, що маючи аналітичні вирази, можна завжди розробити програми для обчислювальної машини і здобути усі необхідні результати.

Розглянемо кривошипно-повзунковий механізм (рис.5).

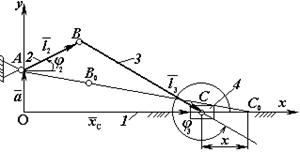
Рис.5

З метою визначення швидкостей і прискорень ланок механізму подамо контур ОАВСО як векторну суму:

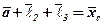. (1)

Проектуючи рівняння (1) на осі Ох і Оу, маємо:

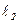cosj₂ + 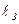cosj₃ = x_c ,

a+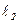sinj₂+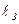sinj₃=0. (2)

Із другого рівняння (2) маємо:

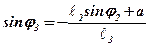. (3)

Як бачимо з рисунка, вектор 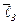може лежати тільки в першій або в четвертій четвертях, тобто cosj₃ – величина завжди додатна. Підставивши значення sin j ₃ (3) у перше рівняння (2), знайдемо величину переміщення:

. (4)

Щоб визначити швидкості, продиференціюємо рівняння (2) за кутом j ₂, після чого отримаємо:

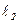– sinj₂ – u₃₂ 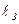sinj₃ = x^¢_c,

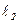cosj₂ + u₃₂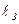cosj₃ = 0, (5)

де 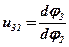– аналог кутової швидкості w₃ шатуна і 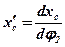– аналог лінійної швидкості v_c повзуна. Аналог швидкості u₃₂ знаходимо з другого рівняння (5) і, підставивши його в перше, визначимо аналог швидкості повзуна x'_c:

,

  .. (6)

Для визначення аналогів кутового прискорення u^¢₃₂ шатуна 3 і прискорення x^¢¢_c повзуна 4 продиференціюємо за j₂ рівняння (5):

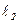– cosj₂ – u²₃₂ 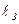cosj₃ - u^¢₃₂ 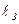sinj₃ = x^¢¢_c ,

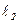– sinj₂ – u²₃₂ 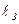sinj₃ + u^¢₃₂ 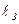cosj₃ = 0. (7)

Із другого рівняння знаходимо аналог кутового прискорення шатуна:

. (8)

Підставивши це значення u^¢₃₂ у перше рівняння (7), дістанемо аналог x^¢¢_c.

Дійсне значення швидкостей w₃ і v_c прискорень a_c, e₃ дорівнюють:

v_c = w₃ x^¢_c , w₃ = w₂ u₃₂,

a_c= w₂² x^¢¢_c + e₂ v_c , e₃ = w₂² u^¢₃₂ + e₂ u₃₂. (9)

3. Завдання кінематичного синтезу плоских механізмів

Залежно від призначення механізму точки ведених ланок повинні мати певні траєкторії, переміщення, швидкості й прискорення. Ці параметри залежать від закону руху ведучої ланки і від параметрів кінематичної схеми, тобто розмірів ланок, які визначають його кінематичну схему. Визначення параметрів кінематичної схеми за відомими кінематичними умовами руху веденої ланки є основним завданням проектування механізмів, оскільки решта етапів проектування мають лише перевірні та допоміжні розрахунки, які дозволяють встановити можливість і доцільність реального виконання здобутої кінематичної схеми механізму.

Далі під синтезом механізмів будемо розуміти сукупність задач про визначення параметрів кінематичної схеми за заданими умовами руху ланок.

Оскільки ці умови різноманітні, то і різноманітні задачі, пов’язані з синтезом механізмів.

1. Задача відтворення заданого закону руху (заданої цільової функції). Ця задача полягає у визначенні таких параметрів кінематичної схеми, які забезпечують рух веденої ланки за заданим законом при певному законі руху ведучої ланки.

2. Задача про відтворення заданої траєкторії. Ця задача полягає у визначенні параметрів кінематичної схеми механізму, в якому одна із точок ланки, що здійснює складний рух, рухається по заданій траєкторії.

4..Умова існування кривошипа в чотириланкових механізмах

Маємо шарнірний чотириланковик ABCD, у якого довжини ланок позначена як a, b, c та d (рис.6). Потрібно визначити умови, при яких ланка AB буде кривошипом, тобто буде повертатися на кут 360°, якщо a<b<c<d. З’єднаємо точки B і D прямою та позначимо відстань BD через f. Тоді з rABD видно:

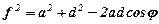, (1)

а з r BCD маємо:

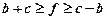, (2)

З рівняння (1) дістаємо

.

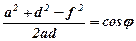Враховуючи нерівності (2), маємо:

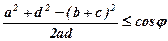; (3)

. (4)

Рис.6

Якщо ланка a повертається на кут 360°, то кут φ набуває значень від 0 до 360° і cosφ змінюється в межах від +1 до -1. Оскільки ліва частина нерівності (3) повинна бути меншою найменшого значення cosφ, а ліва частина нерівності (4) повинна бути більшою найбільшого значення cosφ, то:

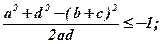
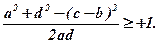
З цих нерівностей маємо:

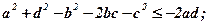
Звідси перенесенням членів отримаємо:

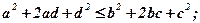
або

Або остаточно:

(5)

(6)

Нерівність (6) може бути записана так:

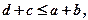
але вона випливає із зазначеної вище умови a<b<c<d, тобто нерівність (6) не дає ніяких нових умов.

З нерівності (5) виходить: щоб у шарнірному чотириланковику, сторони якого задовольняють умову a<b<c<d, ланка а була кривошипом, необхідно щоб сума довжин найменшої та найбільшої ланки була менша або дорівнювала сумі довжин двох інших ланок.

Питання для самоконтролю

1. Що називається кінематичною діаграмою? Які переваги та недоліки має цей метод у порівнянні з методом планів?

2. Як будується діаграма переміщень s=s(φ)?

3. Сутність методу дотичних.

4. За якими формулами визначаються масштаби швидкостей і прискорень μ_v та μ_a?

5. Як визначаються дійсні значення швидкостей і прискорень веденої ланки в усіх положеннях механізму?

6. Як визначаються дійсні швидкості та прискорення точок і кутові швидкості та прискорення ланок при аналітичному методі дослідження?

7. У чому полягають завдання кінематичного синтезу плоских механізмів?

8. Довести умову існування кривошипа в чотириланкових механізмах.

Лекція № 22

Тема: “Кулачкові механізми та їх різновиди”

1. Кулачкові механізми, застосування, переваги та недоліки.

2. Основні типи просторових і плоских кулачкових механізмів.

3. Основні параметри кулачка.

4. Аналіз різноманітних законів рухів штовхача.

1. Кулачкові механізми, застосування, переваги та недоліки

Кулачкові механізми застосовуються у тих випадках, коли в процесі безперервного руху ведучої ланки (кулачка) необхідно за заданим законом змінювати рух веденої ланки і особливо тоді, коли остання під час руху решти ланок повинна тимчасово зупинятися.

Такий характер руху має місце в металорізальних верстатах-автоматах, у пресах, деяких типах ножиць, у розподільних механізмах парових машин з клапанним паророзподілом, у двигунах внутрішнього згорання тощо.

До переваги кулачкових механізмів відносять їх універсальність. Надаючи кулачку ту чи іншу форму, можна дістати майже будь-який рух штовхача з будь-яким законом зміни таких параметрів, як швидкість, прискорення чи траєкторія.

Недоліками кулачкових механізмів є:наявність вищої пари, а отже, значного питомого тиску, що викликає швидке спрацювання кулачків (для запобігання спрацювання кулачки виготовляють із високоякісних матеріалів і відповідним чином обробляють);необхідність силового замикання кулачкової пари, яке втілюється за допомогою пружин.

2..Основні типи плоских і просторових кулачкових механізмів

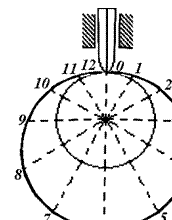
Розрізняють кулачкові механізми просторові й плоскі. У перших кулачок звичайно має форму циліндра з пазом, по якому переміщається ролик штовхача (рис.1).

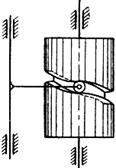
Рис.1

У других ведуча ланка (кулачок) здійснює обертальний або поступальний рух (рис.2, а, б).

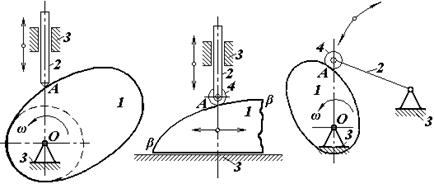
а) б) в)

Рис.2

Будемо розглядати тільки механізми з кулачком, що обертається, як такі, що мають найбільше розповсюдження.

Плоскі кулачкові механізми з кулачком, що обертається, поділяються на дві групи:

1).перша група перетворює обертальний рух кулачка в поступальний рух штовхача (рис.2, а);

2) друга група – обертальний рух кулачка в коливальний рух коромисла (рис.2, в).

Кожна із цих груп за формою елементу веденої ланки поділяється на три підгрупи, в яких кулачок працює:

а) по вістрю;

б) по ролику;

в) по площині.

Кулачкові механізми, які перетворюють обертальний рух у поступальний і працюють по вістрю або ролику, поділяються на:

а) центральні;

б) дезаксіальні.

Центральними називаються такі кулачкові механізми, в яких вісь штовхача проходить через центр обертання кулачка.

У дезаксіальних механізмах вісь штовхача зміщена відносно центра обертання кулачка на деяку величину е, яка називається дезаксіалом.

3. Основні параметри кулачка

Профілем кулачка називається крива, здобута в розрізі елементу кулачка площиною, перпендикулярною до його осі обертання.

Профілі кулачка бувають самі різноманітні. Розглянемо один із них, зображений на рис.3.

Рис.3

Мінімальний радіус кулачка (R_min) – це радіус, що з’єднує центр обертання кулачка з найближчою точкою його профілю.

Максимальний радіус кулачка (R_max) – це радіус, що з’єднує центр обертання кулачка з найвіддаленішою точкою його профілю.

Найбільше переміщення штовхача (h) – різниця довжини максимального і мінімального радіусів кулачка.

Неробочий кут (неробоча фаза) або кут б лижнього стояння (фаза ближнього стояння) (j_о) – це центральний кут, що спирається на дугу ab мінімального радіуса. Під час ковзання по дузі мінімального радіуса штовхач залишається нерухомим і знаходиться в крайньому нижньому положенні.

Кут віддалення (фаза віддалення) (j_в) – це центральний кут, що спирається на дугу bc, яка з’єднує крайні точки дуг мінімального і максимального радіусів кулачка. При ковзанні по дузі bc штовхач починає рухатись і віддаляється на максимальну відстань (переходить із нижнього у верхнє положення).

Кут дального стояння (фаза дальнього стояння) (j_д.с.) – це центральний кут кулачка, що спирається на дугу сd максимального радіуса. Поки штовхач ковзає по дузі сd, він нерухомий і знаходиться на максимальній відстані від центра обертання кулачка О.

Кут повернення (фаза повернення) (j_п) – це центральний кут кулачка, що спирається на дугу da, яка з’єднує крайні точки дуг максимального і мінімального радіусів кулачка. Під час ковзання по дузі da штовхач повертається із верхнього у вихідне (нижнє) положення.

Робочий кут(робоча фаза) (j_р) – це центральний кут кулачка, що дорівнює сумі кутів віддалення, дальнього стояння і повернення:

j_р= j_в+ j_д.с.+j_п.

Сума всіх кутів дорівнює 360⁰:

j_о+ j_в+ j_д.с.+ j_п = j_о+ j_р = 360⁰.

Радіус профілю кулачка R₂ (R¢₂) – радіус дуги, що відповідає фазі віддалення (повернення). Якщо крива, що відповідає фазі віддалення (або повернення) не є дугою кола, то радіус профілю кулачка в цьому випадку буде змінним.

4. Аналіз різноманітних законів руху штовхача

Для проектування профілю кулачка механізму необхідно обрати:

1) кінематичну схему механізму;

2) закон руху веденої ланки (штовхача);

3) деякі основні розміри ланок.

Найпростішим законом руху є рівномірний рух штовхача в обидва боки (рис.4).

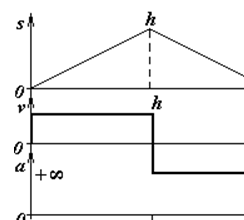Якщо швидкість штовхача в обидва боки однакова, то відрізки нахилені до осі абсцис під однаковими кутами.

Якщо швидкість на початку і в кінці підйому раптово змінює напрямок, то в точках 0 і h на діаграмі v–t цьому відповідають розриви швидкості. Миттьова зміна швидкості викликає нескін-ченно великі прискорення, а в механізмі в цей момент відбуваються жорсткі удари.

Про наявність їх можна зробити висновок і по профілю кулачка. Жорсткі удари виникають у місцях спряження кривих, що не мають спільної дотичної (в точках с і d у вищерозглянутому кулачку на рис.3).

Для того щоб запобігти виникненню жорстких ударів, доводиться відмовлятись від законів руху, що мають розриви на діаграмі швидкостей. Наприклад, обрати закон руху штовхача, зображений на рис.5.

При такому законі в механізмі з’являються м’які удари, оскільки на діаграмі прискорення а–t мають місце розриви.

М’які удари виникають у місцях спряження кривих (що утворюють профіль кулачка), які мають спільну дотичну, але різні радіуси кривизни (у точках a і b у вище розглянутому кулачку на рис.3).

Для безударної роботи механізму необхідно обрати такий закон руху штовхача, при якому на кінематичних діаграмах не було б розривів. Це, зокрема, набір синусоїд.

Питання для самоконтролю

1. Призначення та застосування кулачкових механізмів.

2. Їх переваги та недоліки.

3. Різновиди плоских кулачкових механізмів.

4. Дати означення основним параметрам кулачка: профілю, мінімальному та максимальному радіусам, найбільшому переміщенню штовхача, фазам ближнього та дальнього стояння, віддалення та повернення, робочій фазі, радіусу профілю кулачка.

5. Проаналізувати різноманітні закони руху штовхача.

6. Коли в кулачковому механізмі виникають жорсткі та м’які удари? Як зробити висновок про їх наявність по профілю кулачка?

Лекція № 23

Тема:“Кінематичний аналіз та синтез кулачкових механізмів. Механізми передач”

1. Кінематичне дослідження кулачкових механізмів.

2. Поняття про профілювання кулачка.

3. Механізми передач. Передаточне відношення.

4..Механізми передач з жорсткими ланками. Основні різновиди, їх характеристика.

1. Кінематичне дослідження кулачкових механізмів

Кінематичне дослідження кулачкових механізмів полягає в знаходженні кінематичних параметрів штовхача за весь цикл роботи механізму.

Метою кінематичного дослідження є забезпечення обчисленого, заданого режиму роботи.

Рис.1

Щоб визначити переміщення штовхача, можна було б кожного разу креслити нове положення механізму, в якому кулачок був би повернутий на певний (частіше 30⁰) кут. Але оскільки кулачок має складний профіль, то креслити його декілька разів є надто трудоміською роботою, тому при дослідженні кулачкових механізмів застосовують метод зворотного руху. Розглянемо його сутність.

Кулачок креслиться один раз (у будь-якому положенні) і вважається нерухомим (рис.1). Стояку разом із штовхачем надається обертальний рух навколо осі кулачка з кутовою швидкістю ω кулачка, але в протилежному напрямку.

У такому зворотному русі переміщення штовхача відносно кулачка буде таким же, як і в дійсному русі при нерухомому стояку.

Звідси виходить, щоб визначити переміщення штовхача, досить провести коло мінімального радіуса кулачка, розбити його на рівну кількість частин (6, 8, 12, 24). Відстані від кола мінімального радіуса до точок профілю кулачка, виміряні на продовженнях радіусів, і є переміщеннями штовхача, які відповідають повороту кулачка на певний кут. Відклавши визначені переміщення штовхача в 12 положеннях механізму в масштабах μ_s та μ_φ, ми дістанемо залежність s=s(φ).

Швидкість і прискорення штовхача визначають одноразовим і дворазовим графічним диференціюванням цієї залежності (див. лекц.№21).

2. Поняття про профілювання кулачка

Завдання кінематичного синтезу кулачкового механізму обернене завданню аналізу й полягає в проектуванні профілю кулачка за діаграмою s=s(φ).

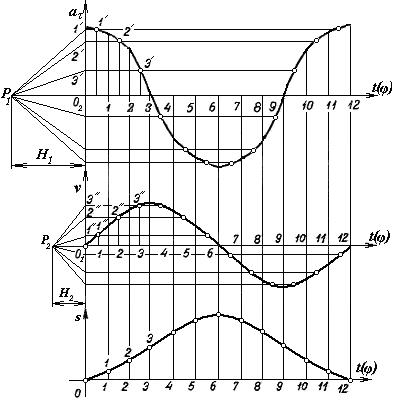
Рис.2

При синтезі кулачкового механізму зазвичай бувають відомі його кінематична схема, основні розміри кулачка і закон руху штовхача, заданий однією із кінематичних діаграм. Невідомим є тільки профіль кулачка, який і треба знайти.

Нехай маємо закон a=a(φ). Тоді масштаби μ_s і μ_φ відомі. Швидкість і переміщення штовхача визначається одноразовим і дворазовим графічним інтегруванням цієї залежності (рис. 2).

Для цього із середини кожного інтервалу 0–1, 1–2, 2–3, … проводимо горизонтальні прямі до перетину їх з віссю ординат. Дістанемо ряд точок 1¢, 2¢, 3¢, …. Сполучивши їх з полюсом Р₁, обраному на довільній відстані H₁ від початку координат, отримаємо промені Р₁1¢, Р₁2¢, Р₁3¢, …. Нижче обираємо координатні осі для побудови залежності v=v(φ). Розділяємо вісь φ на стільки ж інтервалів, на кожному із яких паралельно променям Р₁1¢, Р₁2¢, Р₁3¢,... проводимо хорди. З’єднавши здобуті точки плавною кривою, дістанемо діаграму v=v(φ) у масштабі μ_φ:

μ_v=H₁·μ_a·μ_φ,

де Н₁ – полюсна відстань у мм.

Аналогічно проінтегрувавши залежність v=v(φ), дістанемо діаграму s=s(φ) у масштабі μ_s=H₂·μ_v·μ_φ (рис.2).

Потім креслимо коло мінімальним радіусом профілю кулачка (R_min), розділяємо його на стільки ж частин, скільки інтервалів на осі абсцис (частіше 12). На продовженні радіусів у кожному положенні відкладаємо переміщення штовхача, отримані із діаграми s=s(φ). Сполучивши здобуті точки плавною кривою, знайдемо шуканий профіль кулачка (рис.3).

3.Механізми передач. Передаточне відношення

Механізми, призначені для відтворення обертального руху між двома довільно розміщеними в просторі осями, називаються механізмами передачі обертального руху або скорочено механізмами передач.

Механізми передач мають своїм завданням відтворення заданого передаточного відношення між двома ланками.

Для того, щоб виконувати кінематичний аналіз механізмів передач, необхідно ввести поняття передаточного відношення.

Передаточним відношенням називають відношення кутової швидкості ведучої ланки до кутової швидкості веденої ланки і позначають літерою u з відповідними індексами.

Таким чином, якщо ведучою є ланка 1, то:

Ще передаточне відношення може визначатись через кількість обертів n ланок:

Якщо ведена і ведуча ланки обертаються в один бік (наприклад, у зубчатій передачі з внутрішнім зачепленням), то передаточне відношення вважається додатним.

Якщо ведене і ведуче колеса обертаються в різні боки (наприклад, у зубчатої передачі із зовнішнім зачепленням), то передаточне відношення вважається від’ємним.

4. Механізми передач із жорсткими ланками. Основні різновиди, характеристика

До механізмів передач із жорсткими ланками відносяться зубчаті зачеплення, фрикційні передачі. Глибше вони розглядаються в модулі “Розрахунок вузлів та деталей машин” курсу “Технічна механіка”. Тому дуже коротко зупинимось на цих різновидах передач.

Розглянемо зубчате зачеплення, зображене на рис.4.

Модуль зачеплення – це частина діаметра ділильного кола, що припадає на один зуб. Модуль зачеплення визначається за формулою:

,

де d – діаметр ділильного кола.

Оскільки =t z, а з іншого боку =π d, то:

де t – осьовий крок.

Тоді:

.

Передаточне відношення зубчатого зачеплення:

.

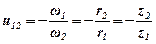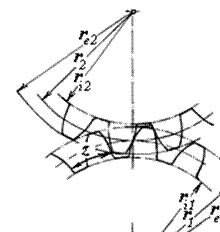
r_i – радіус кола западин;

r_e – радіус кола виступів;

r – радіус ділильного кола.

Рис.4

Зубчатий механізм, який складається з трьох і більше зубчатих коліс (з нерухомими осями) і стояка, називається зубчатим рядом.

Передаточне відношення зубчатого ряду визначається як добуток передаточних відношень окремих передач:

де k – кількість зовнішніх зачеплень.

Може бути декілька схем розміщення зубчатих коліс.

Одноступінчатезачеплення (рис.5). При такій схемі зачеплень, передаточне відношення:

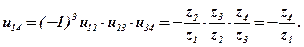
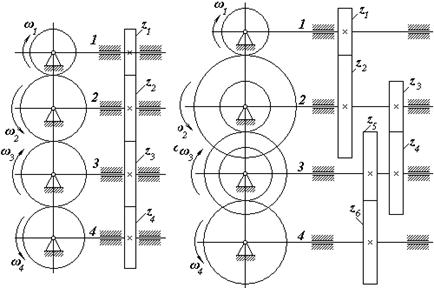
Рис.5 Рис.6

Як бачимо, проміжні колеса z₂ та z₃ не впливають на величину передаточного відношення, але впливають на його знак (напрямок руху).

Багатоступінчате зачеплення (рис.6). У цьому випадку передаточне відношення визначимо як:

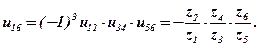
Таким чином, у багатоступінчатому зачепленні всі зубчаті колеса впливають на величину передаточного відношення.

До механізмів передач з жорсткими ланками відноситься рейкове зачеплення. У нього передаточне відношення дорівнює нескінченності або нулю в залежності від того, яка ланка буде ведучою (колесо чи рейка), оскільки рейка рухається поступально, і її кутова швидкість дорівнює нулю.

Черв’ячна передача застосовується для передачі обертальних рухів між перехресними валами. Одна ланка називається черв’яком, інша – черв’ячним колесом. Передаточне відношення визначається за формулою:

де z₁ – кількість заходів черв’яка, z₂ – кількість зубів черв’ячного колеса.

Питання для самоконтролю

1. У чому полягає кінематичне дослідження кулачкових механізмів?

2. Яку мету переслідує кінематичний аналіз кулачкового механізму?

3. Сутність методу зворотного руху? Як він застосовується для побудови діаграми переміщення штовхача s=s(φ)?

4. Як побудувати залежності v=v(φ) або а=а(φ)?

5. У чому полягає синтез кулачкового механізму? Які вихідні дані для цього мають бути?

6. Сутність графічного інтегрування методом хорд.

7. Побудова профілю кулачка за діаграмою s=s(φ).

8. Які механізми називаються механізмами передач? Яке їх основне завдання?

9. Що називається передаточним відношенням? Як визначається його знак?

10. Різновиди передач з жорсткими ланками, їх коротка характеристика.

11. Як визначається передаточне відношення зубчатого ряду? У випадках одноступінчатого і багатоступінчатого зачеплень?

12. Як визначаються передаточні відношення рейкового зачеплення та черв’ячної передачі?

Лекція № 24

Тема: “Фрикційні та епіциклічні механізми, їх кінематика”

1.Фрикційні механізми. Варіатори швидкостей.

2.Епіциклічні механізми, їх характеристика.

3.Класифікація епіциклічних механізмів.

4.Визначення передаточних відношень планетарного і диференціального механізмів.

1. Фрикційні механізми. Варіатори швидкостей

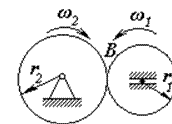Фрикційними називають механізми, в яких для передачі крутного моменту використовують сили тертя. Фрикційна передача складається з двох циліндричних або конічних котків, притиснутих один до одного з певним зусиллям (рис.1).

Передаточне відношення фрикцій-ної передачі:

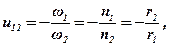
де r₁ та r₂ – радіуси ведучого та веденого котків.

Швидкість точки В визначається за формулою:

Механізми, які забезпечують плавну зміну передаточного відношення, називають механізмами безступінчатих передач або варіаторами швидкостей.

Розглянемо схему лобового фрикційного варіатора (рис.2).

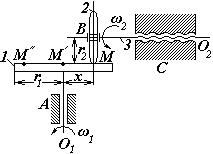
Рис.2

Диск 1 жорстко зв’язаний з віссю О₁, яка обертається в нерухомому підшипнику. Диск 1 входить у вищу кінематичну пару з роликом 2. Останній утворює обертальну кінематичну пару В з ланкою 3. Ролик 2 за допомогою гвинтової пари С можна переміщати вздовж осі О₂. Точка М дотикання елементів ланок 1 і 2 може займати різні положення, що визначаються відстанню х.

Тоді передаточне відношення дорівнює:

.

У положенні М' передаточне відношення u₂₁=0. При переміщенні точки дотикання ланок М за точку М', наприклад, у положення М'', диск 1 змінює напрямок обертання. Таким чином, передаточне відношення плавно змінюється в межах:

.

Більш глибоко фрикційні передачі вивчаються в модулі “Розрахунок вузлів та деталей машин” курсу.

2. Епіциклічні механізми, їх характеристика

Зубчаті механізми, до складу яких входять рухомі осі зубчатих коліс, називаються епіциклічними.

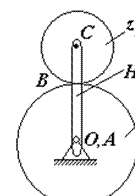Найпростіший епіциклічний механізм зображений на рис.3.

Колесо z₂, вісь якого переміщається в просторі, називається сателітом.

Зубчате колесо z₁, навколо якого обертається сателіт, називається центральним або сонячним.

Ланка Н, яка несе на собі вісь сателіта, називається водилом.

Необхідно відзначити, що в будь-якому епіциклічному механізмі ніяких інших ланок (окрім сателітів, сонячних коліс і водил) не може бути. Якщо є інші ланки, то вони не входять до складу епіциклічного механізму, а утворюють між собою кінематичний ланцюг, який приєднується до епіциклічного механізму.

3. Класифікація епіциклічних механізмів.

Епіциклічні механізми поділяються на:

1) планетарні;

2) диференціальні.

Планетарним називається епіциклічний механізм, ступінь рухомості якого дорівнює одиниці.

Якщо ступінь рухомості епіциклічного механізму більший одиниці, то такий механізм називається диференціальним або просто диференціалом.

Ступінь рухомості механізму, зображеного на рис.3:

W = 3n– 2p₅ –p₄ = 3∙3–2∙3–1 = 2.

Отже, цей механізм є диференціальним. Якщо в ньому закріпити сонячне колесо z₁ нерухомо, то він перетвориться на планетарний:

W = 3n– 2p₅ –p₄ = 3∙2–2∙2–1 = 1.

Наведемо ще один приклад (рис.4).

Ступінь рухомості механізму:

W = 3n–2p₅–p₄ = 3∙4–2∙4–2 = 2.

Отже, зображений на рис. 4 механізм диференціальний.

Тип механізму можна визначити і за його зовнішнім виглядом. Якщо в епіциклічному механізмі всі зубчаті колеса рухомі, то він буде диференціальним. Якщо ж є нерухоме колесо – то планетарним.

Призначення планетарних механізмів – відтворювати великі (або малі) передаточні відношення. Вони можуть відтворювати дуже великі (чи дуже малі) передаточні відношення при малих габаритах механізму і малій кількості зубів зубчатих коліс.

Призначення диференціальних механізмів – складання чи розкладання рухів.

Епіциклічні механізми застосовуються в автомобілях, тракторах, обчислювальних, сільськогосподарських та інших машинах.

4. Визначення передаточних відношень планетарного і диференціального механізмів

Нехай маємо будь-яку кінематичну схему епіциклічного механізму. Кутові швидкості кожного зубчатого колеса при обертанні відносно водила можна визначити як різницю відповідних кутових швидкостей:

…………………

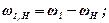
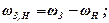
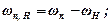
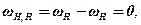
де ω₁ – кутова швидкість колеса z₁, ω_H – кутова швидкість водила, ω_1Н – кутова швидкість колеса z₁ відносно водила і т.д.

Поділивши два рівняння одне на інше, дістанемо передаточне відношення між відповідними колесами механізму при зупиненому водилі:

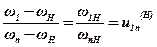
або

Верхній індекс вказує на номер нерухомої ланки, при якій визначається передаточне відношення.

Ця формула називається формулою Вілліса за ім’ям англійського вченого, який вивів її в 1841 р. Формула Вілліса універсльна для аналізу будь-яких епіциклічних механізмів.

Для планетарних механізмів формула дещо скорочується. Нехай ω_п =0, тоді:

або остаточно маємо:

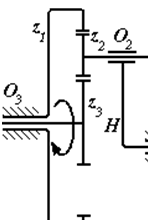
Приклад 1. Виначити передаточне відношення u_3H від вала О₃ до вала О_н (рис.5).

Розв’язання. Визначимо ступінь рухомості механізму:

W = 3n– 2p₅ –p₄ = 3∙3–2∙3–2 = 1.

Отже, цей механізм планетарний, тому застосуємо скорочену формулу Вілліса:

.

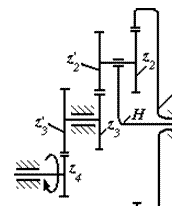Приклад 2. Визначити передаточне відношення u_4H механізму, зображеного на рис.6, якщо z₁ =90; z₂ =30; z₂' =40; z₃ =20; z ₃' =50; z₄ =25.

Ступінь рухомості механізму:

W = 3n– 2p₅ –p₄ = 3∙4–2∙4–3 = 1.

На рис.6 показаний складний редуктор, у якого колеса z₁, z₂, z₂' та z₃ утворюють планетарний механізм, а колеса z₄ і z₃' – одноступінчату передачу з нерухомими осями.

Загальне передаточне відношення визначиться так:

Приклад 3. Визначити передаточне відношення u_H4 редуктора, зображеного на рис.7, якщо z₁ =80; z₂ =40; z₂' =40; z₃ =20; z₃' =50; z₄ =25.

Ступінь рухомості редуктора:

W = 3n– 2p₅ –p₄ = 3∙4–2∙4–3 = 1.

Зображений на рис.7 зубчатий механізм складний, до складу якого входить планетарна частина (z₁, z₂, z₂', z₃) та передача з внутрішнім зачепленням (z₃', z₄). Тоді:

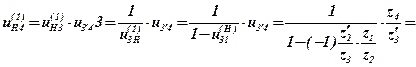
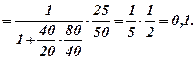
Питання для самоконтролю

1. Які механізми називаються фрикційними? Як визначається їх передаточне відношення?

2. Дати означення варіатору швидкостей.

3. Зобразити схему лобового фрикційного варіатора швидкості й пояснити принцип його роботи.

4. Дати означення епіциклічному механізму, сателіту, водилу та сонячному колесу.

5. Як класифікуються епіциклічні механізми?

6. Який механізм називається планетарним, диференціальним? Їх призначення і сфера застосування.

7. Як визначається передаточне відношення епіциклічного механізму?

Лекція № 25

Тема: “Універсальний шарнір. Механізми передач з гнучкими ланками. Хвильові передачі”

1..Універсальний шарнір. Особливості будови та принцип роботи. Передаточне відношення.

2. Карданні передачі.

3. Механізми передач з гнучкими ланками.

4. Загальні відомості про хвильові передачі.

1. Універсальний шарнір. Особливості будови та принцип роботи. Передаточне відношення

Універсальний шарнір, або шарнір Гука, служить для з’єднання валів, коли кут між ними змінюється на ходу і близький до 180°.

Схема універсального шарніра зображена на рис.1.

В універсальному шарнірі осі всіх (чотирьох) шарнірів A, B, D та Е перетинаються в одній точці О.

Ланки 1 і 3, які називаються вилками, однакові і з’єднуються хрестовиною 2. Пальці хрестовини входять у відповідні отвори вилок. Кожна вилка з’єднана зі стояком нерухомими шарнірами, осі яких перетинаються під кутом α.

Рис.1

Нехай ведуча вилка 1 обертається рівномірно з кутовою швидкістю 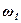, тоді швидкість точки А (центр шарніра):

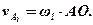
Якщо ж тепер цю точку А віднести до веденої вилки 3, то колова швидкість буде:

де – кутова швидкість веденої вилки 3; AС – перпендикуляр, опущений із точки А на вісь обертання веденої вилки 3.

Але:

Отже:

або

.

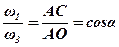Звідси:

Якщо повернемо універсальний шарнір на кут 90°, то:

.

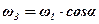Таким чином, в універсальному шарнірі при сталій кутовій швидкості 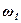ведучої вилки 1 ведена вилка 3 обертається нерівномірно, причому передаточне відношення змінюється в межах від cosα до .

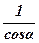Середня кутова швидкість ω_3ср веденої вилки 3 дорівнює сталій кутовій швидкості ω₁ ведучої вилки 1, оскільки за час одного оберту вилки 1 вилка 3 також здійснить один оберт.

2. Карданні передачі

Зв’язок між валом відбору потужності трактора і приймальним валом сільськогосподарської машини здійснюється за допомогою карданної передачі.

Карданна передача складається із декількох валів, з’єднаних універсальними шарнірами. Бувають дво-, три- і чотиришарнірні карданні передачі.

Найпоширенішою карданною передачею є тришарнірна (рис.2). Вона складається із вала відбору потужності 1, телескопічного вала 2, проміжного вала 3, запобіжної муфти 4, приймального вала сільськогосподарської машини 5, універсальних шарнірів А, В і С.

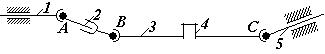
Рис.2

Телескопічне з’єднання валів виконується у вигляді рухомого шліцьового з’єднання (або квадратного вала та труби з квадратним отвором) і забезпечує осьове переміщення валів карданної передачі при пересуванні сільськогосподарської машини по нерівному полю та на поворотах.

3. Механізми передач з гнучкими ланками

До механізмів передач з гнучкими ланками відносяться передачі:пасова;канатна;ланцюгова тощо.

До переваг пасових передач належать:

- можливість передачі рухів на відстані;

- плавність і безшумність роботи;

- запобігання перевантаженню механізмів за рахунок проковзування пасів;

- можливість роботи з високими швидкостями;

- невисока вартість.

Їх недоліками є:

- значні габарити;

- необхідність пристроїв для натягування паса у передачах з малою міжосьовою відстанню;

- мала довговічність пасів у швидкохідних передачах;

- неминучість деякого пружного ковзання паса.

Передачі з гнучкими ланками широко застосовуються у вигляді ланцюгових передач, в яких зубчаті зірочки входять у зачеплення із ланками ланцюга. Такі механізми застосовують у сільськогосподарських машинах, транспортерах, гірничих машинах тощо.

Ланцюгові передачі в порівнянні з пасовими відрізняються:

- відсутністю ковзання;

- високим коефіцієнтом корисної дії;

- меншими габаритами.

Але в той же час вони працюють в умовах відсутності рідинного тертя і, як наслідок, з неминучим спрацюванням, а також потребують більш високої точності установки валів, ніж клинопасові. До того ж швидкість руху ланцюга, особливо при малій кількості зубів зірочок, не стала, що викликає нерівномірність обертання зірочок.

При передачі руху гнучкою ланкою за допомогою круглих шківів (рис.3) передаточне відношення дорівнює:

,

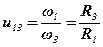тобто передаточне відношення дорівнює оберненому відношенню радіусів R₁ і R₃ шківів 1 і 3.

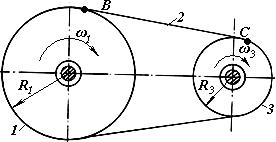
Рис.3.

Механізм передачі з гнучкою ланкою, зображений на рис.3, носить назву відкритої передачі, а на рис.4 – перехресної. Передаточне відношення останньої визначається:

.

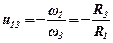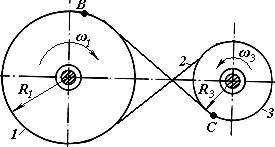
Рис.4.

Механізми передач з гнучкими ланками досить глибоко розглядаються в модулі “Розрахунок вузлів та деталей машин” курсу технічної механіки.

4. Загальні відомості про хвильові передачі

Розглянемо конструкцію хвильової передачі, зображеної на рис.5.

Так само, як і планетарна, хвильова передача складається з трьох основних ланок: 1 – генератор хвиль, який виконаний у вигляді водила з двома роликами; 2 – гнучке колесо – пружна тонкостінна склянка, основа якої з’єднана з веденим валом, а на потовщеному вінці поблизу торця нарізані зубці; 3 – нерухоме жорстке колесо з внутрішніми зубцями.

Рис.5

Модулі зачеплення коліс 2 і 3 однакові, а кількість зубів гнучкого колеса 2 менша, ніж колеса 3 (z₂<z₃). Різниця z₃-z₁=W характеризує кількість хвиль деформації гнучкого колеса. Оптимальне значення W=2.

Ділильні діаметри теж неоднакові: d₃>d₂. У вільному стані (без генератора) колеса розміщені концентрично з рівномірним зазором між зубцями. При встановленому генераторі останній деформує гнучке колесо в радіальному напрямку, надаючи йому форму еліпса: по великій осі еліпса (зона А) зубці зачіпляються на повну робочу висоту, а по малій осі (зона В) – між вершинами зубів утворюється радіальний зазор, а в зоні С зачеплення проміжне.

У процесі обертання генератора форма гнучкого колеса залишається близькою до описаної і лише змінює свої координати, тобто зачепле

Дата добавления: 2014-10-23