Побудова плану прискорень

Аналогічно побудові плану швидкостей будується план прискорень.

Нехай маємо двоповодкову групу ВСD (рис.1,а).

Вихідними даними для неї є вектори прискорень у точках В та D (у відкритих кінематичних парах) та і довжини ланок 2 та 3. Необхідно визначити прискорення точки С.

Рух точки С розглядаємо як складний, який складається із переносно-поступального зі швидкістю та прискоренням точки В або D і відносно-обертального навколо цих точок.

Запишемо векторні рівняння:

де 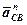, – нормальні прискорення у відносному русі; , – тангенціальні (дотичні) прискорення у тому ж русі.

Розв’язуючи рівняння, маємо:

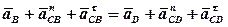. (3)

У рівнянні (3) відомі за величиною і напрямком прискорення точок В та D, тобто та 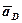. Вектори нормальних прискорень та визначаються за формулами:

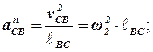
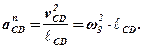
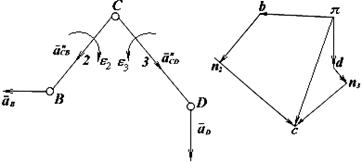
а) б)

Рис.1

Швидкост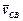і і 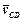можуть бути визначені із плану швидкостей. Тоді:

Вектор прискорення 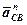напрямлений із точки С у точку В паралельно ланці ВС (див. рис.1,а), а вектор прискорення – від точки С у точку D паралельно ланці СD.

Таким чином, нормальні прискорення відомі за величиною і напрямком. Вектори і відомі тільки за напрямком: вони напрямлені перпендикулярно до ланок відповідно ВС і CD. Величини їх можна визначити графічно, побудовою плану прискорень.

Обираємо за полюс точку π і відкладаємо відрізки πb та πd у масштабі μ_а, що зображають вектори прискорень та (рис.1,б). Так само, як і для плану швидкостей, при виборі масштабу μ_а плану прискорень керуються зручністю обчислень і графічних побудов:

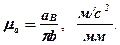
Далі визначаємо та і відкладаємо відповідно із точок b та d відрізки bn₂ та dn₃:

паралельно ланкам 2 і 3, а із точок n₂ та n₃ проводимо прямі, перпендикулярні до ланок ВС і CD (напрямки тангенціальних складових прискорень). Точка перетину і дасть кінець шуканого вектора :

Маючи план прискорень, можна визначити кутові прискорення ε₂ та ε₃ ланок 2 та 3. Їх модулі дорівнюють:

або

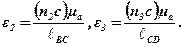
де 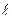_BC, 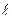_CD – довжини ланок відповідно 2 та 3 у метрах.

Напрямки кутових прискорень визначається таким чином. Подумки переносимо вектори та , що зображаються відрізками n₂с та n₃c, із плану прискорень у точку С, і бачимо, що напрямок ε₂ збігається з напрямком ходу годинникової стрілки, а напрямок ε₂ протилежний ходу годинникової стрілки.

Методи пропорційних відрізків та подібних фігур справедливі й при побудові плану прискорень.

2. Приклад кінематичного аналізу плоского механізму методом планів

Виконати кінематичне дослідження механізму, зображеного на рис.2,а методом планів швидкостей і прискорень.

Вихідні дані: закон руху ведучої ланки у вигляді ω=const і кінематична схема механізму, побудована в масштабі μ_l.

Спочатку виконаємо структурний аналіз механізму. Цей шарнірно-важільний механізм ІІ класу ІІ порядку складається із двох груп Ассура ABD та CEF та однієї ведучої групи, до складу якої входить стояк та кривошип 1.

Дата добавления: 2014-10-23