Побудова плану прискорень

План

План

План

План

План

План

1.Додавання поступальних рухів.

2.Додавання обертальних рухів навколо двох паралельних осей.

3.Додавання обертальних рухів навколо осей, які перетинаються.

1. Додавання поступальних рухів

Як було зазначено вище, складним називається такий рух твердого тіла, коли воно рухається відносно рухомих осей Oxyz (рис.1), а останні здійснюють деякий рух відносно нерухомих осей О₁х₁у₁z_1.

Рис.1

Основними кінематичними характеристиками складного руху є його поступальні та кутові швидкості та прискорення. Ми зупинимось на визначенні тільки поступальних та кутових швидкостей.

Якщо відносний рух твердого тіла є поступальним зі швидкістю 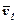, а переносний рух також поступальний зі швидкістю , то очевидно, згідно теореми про додавання швидкостей будемо мати: , тобто абсолют-ний рух твердого тіла також буде поступальним.

Отже, при додаванні поступальних рухів із швидкостями 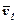і результуючий рух тіла також буде поступальним зі швидкістю:

.

2. Додавання обертальних рухів навколо двох паралельних осей

Нехай диск 1 обертається навколо осі О₁а, закріпленої на кривошипі 2, який у свою чергу обертається навколо осі О₂в (рис.2).

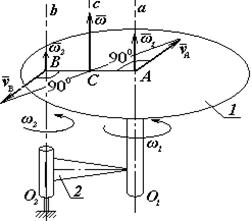Рис. 2

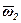Розглянемо спочатку випадок, коли диск 1 і кривошип 2 обертаються в один бік із швидкостями відповідно ω₁ і ω₂. Зобразимо кутові швидкості у вигляді векторів і ,напрямлених вздовж осей О₁а і О₂в. Як бачимо, диск бере участь одночасно в двох обертаннях: навколо осі О₁а з кутовою швидкістю ω₁ (відносний рух) і разом з кривошипом 2 навколо осі О₂в з кутовою швидкістю ω₂ (перенос-ний рух).

Точка В дістає швидкість тільки від обертання відносно осі О₁а, а отже, ν_В=ω₁АВ 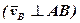. Аналогічно ν_А=ω₂АВ 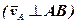. Швидкості і точок А і В паралельні одна одній і напрямлені в протилежні боки. Миттьовий центр швидкостей у даному випадку буде в точці С, через яку проходить миттьова вісь Сс обертання диска.

Тоді:

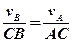або .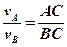

Підставивши значення швидкостей ν_В і ν_А,перепишемо співвідношення:

.

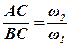Результуючим рухом є обертання навколо миттьової осі Сс. Визначимо модуль миттьової кутової швидкості ω.

Швидкість точки В за модулем, з одного боку:

ν_В=ω₁АВ,

а з іншого боку

ν_В=ωВС.

Звідси:

Підставивши замість відношення його значення, дістанемо остаточно:

Отже, при додаванні двох напрямлених в один бік обертальних рухів навколо паралельних осей утворюється обертання навколо миттьової осі з абсолютною кутовою швидкістю, яка дорівнює сумі кутових швидкостей першого і другого обертань.

Положення миттьової осі Сс визначається із рівності:

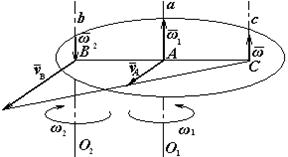Рис.3

Якщо диск і кривошип обертаються в різні боки (рис.3), то швидкості і напрямлені в один бік. Миттьовий центр швидкостей лежить на продовженні відрізка АВ. Тоді для модуля швидкості точки В маємо:

ν_В=ω₁АВ=ω ВС.

Звідси:

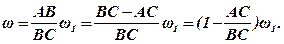
Підставивши замість останнього відношення його значення (див. вище), дістанемо остаточно:

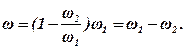
Отже, при додаванні двох напрямлених у протилежні боки обертальних рухів навколо паралельних осей також утворюється обертання навколо миттьової осі, але з абсолютною швидкістю, яка дорівнює різниці кутових швидкостей першого і другого обертань.

Якщо = –, тобто диск і кривошип обертаються з однаковою кутовою швидкістю, але в протилежні боки, то в такому випадку говорять про пару обертань. Миттьовий центр швидкостей знаходиться в нескінченності, й усі точки диска в даний момент будуть мати однакові швидкості. Отже, коли = –, рух диска буде поступальним.

3. Додавання обертальних рухів навколо осей, які перетинаються

Нехай тіло обертається навколо осі О₁а, закріпленої на кривошипі 2, який обертається навколо осі О₂в. Причому осі перетинаються в деякій точці С (р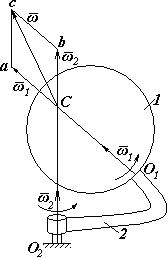ис.4).

Рис.4

Отже, тіло 1 бере участь одночасно в двох обертаннях: навколо осі О₁а з кутовою швидкістю (відносний рух) і разом з кривошипом 2 навколо осі О₂в з кутовою швидкістю 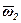(переносний рух). Якщо вектори і 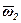перенесемо в точку С перетину осей і знайдемо їх геометричну суму, то визначимо абсолютну швидкість тіла:

.

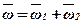Вектор 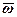напрямлений вздовж прямої Сс, яка проходить через точку С перетину осей обертання, і є не що інше, як миттьова вісь обертання тіла.

Отже, при додаванні двох обертальних рухів навколо осей, що перетинаються, абсолютна кутова швидкість тіла дорівнює геометричній сумі кутових швидкостей у відносному і переносному рухах.

Задача. Зубчатий механізм (рис.5) складається з двох зубчатих коліс 1 і 2 радіусами відповідно r₁ і r₂ та водила ОО₁, яке обертається з кутовою швидкістю ω. Колесо 1 нерухоме, а колесо 2 вільно насаджене на палець О₁ водила. Необхідно визначити абсолютну кутову швидкість 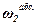і кутову швидкість відносно водила 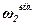колеса 2.

Рис.5

Розв'язання. Оскільки точка С колеса 2 є точкою зчеплення з нерухомим колесом 1, вона в даний момент часу нерухома. Отже, точка С – миттьовий центр швидкостей колеса 2.

Обертання водила будемо розглядати як переносний рух для колеса 2. Побудуємо перпендикулярно ОО₁ вектори 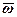, 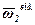і 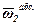переносної, відносної і абсолютної кутових швидкостей зубчатого колеса 2 (див. рис.5).

Скориставшись співвідношеннями, маємо:

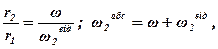
звідки:

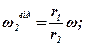
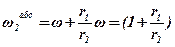ω.

Питання для самоконтролю

1.Як додаються два поступальні рухи?

2.Як додати два обертальні рухи, напрямлені в один бік? Довести.

3.Як додати два обертальні рухи, напрямлені в різні боки? Довести.

4.Чому дорівнює абсолютна кутова швидкість тіла при додаванні двох обертальних рухів навколо осей, що перетинаються?

КІНЕМАТИКА МЕХАНІЗМІВ ТА МАШИН

Лекція № 16

Тема: “Структура та класифікація механізмів. Основні поняття та визначення”

1. Основні поняття та визначення механізму.

2. Класифікація кінематичних пар.

3. Умовне зображення ланок та кінематичних пар.

4. Кінематичний ланцюг, різновидності кінематичних ланцюгів.

1. Основні поняття та визначення механізму

Будь-який механізм складається з окремих деталей (тіл). У механізмах стаціонарного типу одні деталі нерухомі, інші рухаються якимось чином відносно них.

Кожна рухома деталь або група деталей, що утворюють одну жорстку рухому систему тіл, носить назву рухомої ланки механізму.

Всі нерухомі деталі утворюють одну жорстку нерухому систему тіл, яка називається нерухомою ланкою або стояком.

Таким чином, у будь-якому механізмі є одна або декілька рухомих ланок і лише одна нерухома.

З’єднання двох ланок, що дотикаються, яке допускає їх відносний рух, називається кінематичною парою.

Поверхні, лінії або точки ланки, по яких вона може дотикатись до інших ланок, утворюючи при цьому кінематичну пару, називаються елементами ланки.

Зв’язана система ланок, що утворюють між собою кінематичні пари, називається кінематичним ланцюгом.

Обмеження, накладені на відносний рух кожної ланки, називаються умовами в’язі в кінематичних парах.

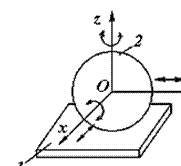
Кожне тверде тіло, що вільно рухається в просторі має 6 ступенів вільності. Якщо забрати один рух, тобто накласти на тіло одну в’язь, то воно буде мати 5 ступенів вільності, наприклад, куля на площині (рис.1).

Очевидно, що кількість умов в’язі може бути тільки цілим числом і меншим шести (при S=6 ланки не можуть рухатись) і такою, що дорівнює або більше одиниці (оскільки при S<1 дві ланки не будуть дотикатися і будуть рухатися в просторі незалежно одна від одної), тобто:

1≤S≤5.

Отже, кількість ступенів вільності визначаються за формулою:

Н=6–S.

2. Класифікація кінематичних пар

Кінематичні пари класифікуються за трьома ознаками:

1) характером відносного руху ланок;

2) формою елементів ланок;

3) кількістю ступенів вільності.

1. За характером відносного руху ланок кінематичні пари поділяються на:

а) плоскі;

б) просторові.

Плоскими парами називають такі, в яких точки ланок, що утворюють кінематичну пару, описують траєкторії, які лежать в одній або паралельних площинах.

Просторовими парами називають такі, в яких точки ланок, що утворюють кінематичну пару, описують неплоскі траєкторії або траєкторії, які лежать у перетинних площинах.

2. За формою елементівланок кінематичні пари поділяються на:

а) вищі;

б) нижчі.

Вищою кінематичною парою називається така, дотикання ланок якої відбувається по лінії або в точці. Іншими словами, елементом якої є лінія або точка (наприклад, кулачкова та зубчата пари).

Нижчою кінематичною парою називається така, дотикання ланок якої відбувається по поверхні. До неї відносяться поступальна і обертальна пари.

Перевагою нижчих пар є їх відносно мале спрацювання, а недоліком – більша, ніж у вищих парах, втрата енергії на тертя в рівних умовах.

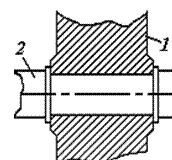3. За кількістю ступенів вільності кінематичні пари поділяються на 5 класів у просторовому русі. Причому клас пари визначається кількістю умов в’язі, накладних на відносний рух ланок.

Розглянемо обертальну кінематичну пару (рис.2). Таке з’єднання ланок допускає один рух – обертання ланки 2 відносно ланки 1, а отже, накладено 5 умов в’язі. Тому ця кінематична пара п’ятого класу. Куля на площині – це кінематична пара першого класу (рис.1).

3.Умовне зображення ланок та кінематичних пар

Спочатку розглянемо, як умовно зображаються ланки механізмів на кінематичних схемах (таблиця 1).

Таблиця 1.

Умовне зображення	Ланки
	стержень, ланка простої конфігурації
	складана ланка
	повзун
	стояк
	зубчате колесо
	кулачок

Кінематичні пари на схемах позначаються літерами латинського алфавіту, а ланки, що їх утворюють, цифрами. Умовне зображення пар подано в таблиці 2.

Таблиця 2.

Умовне зображення	Кінематичні пари
Нижчі:
	обертальна ланки можуть вільно переміщатись у площині лише в сукупності при будь-якому відносному положенні
	обертальна ланка 1 закріплена нерухомо, що обумовлює можливість обертального руху іншої ланки 2 в спільній площині
	поступальна обидві ланки вільно рухаються в площині при довільному відносному положенні
	поступальна ланка 1 закріплена нерухомо, що дозволяє ланці 2 здійснювати поступальний рух відносно неї
Вищі:
	ланки 1 і 2 вільно рухаються в площині при будь-якому відносному положенні
	ланка 2 закріплена нерухомо, а ланка 1 обертається навколо неї

4. Кінематичний ланцюг, різновиди кінематичних ланцюгів

Кінематичним ланцюгом називається зв’язана система ланок, які утворюють між собою кінематичні пари.

Кінематичні ланцюги поділяються на:

1) прості;

2) складні.

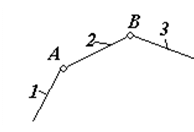Простим називається такий кінематичний ланцюг, кожна ланка якого входить не більше, ніж у дві кінематичні пари (рис.3).

Складним називається кінематичний ланцюг, в якому є хоча б одна ланка, що входить більше, ніж у дві кінематичні пари (рис.4).

Прості й складні кінематичні ланцюги в свою чергу поділяються на закриті й відкриті.

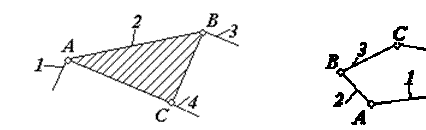
З акритим називається кінематичний ланцюг, кожна ланка якого входить принаймні в дві кінематичні пари (рис.5).

Відкритим називається кінематичний ланцюг, в якому є ланки, що входять тільки в одну кінематичну пару (рис.3, 4).

Тепер можемо дати ще одне означення механізму.

Механізмом називається такий кінематичний ланцюг, в якому при заданому русі однієї або декількох ланок решта здійснюють однозначно визначальні рухи.

Ланки, які рухаються за заданим законом, називаються ведучими. Решта рухомих ланок у механізмі – ведені.

Щоб вивчити рух механізму, недостатньо знати його структуру, тобто кількість ланок, кількість і класи кінематичних пар. Необхідно також знати розміри окремих ланок, які впливають на рух, взаємне їх положення тощо. Тому при вивченні руху ланок механізму складають його кінематичну схему, яка є його кінематичною моделлю.

Кінематична схема механізму будується в обраному масштабі з точним дотриманням всіх розмірів і форм, від яких залежить рух.

Питання для самоконтролю

1. Дати означення рухомій ланці, стояку, кінематичній парі, елементам ланок, кінематичному ланцюгу, умовам в’язі.

2. За якими ознаками класифікуються кінематичні пари?

3..Дати означення плоскій та просторовій, вищій та нижчій кінематичним парам.

4. Як визначається клас кінематичної пари?

5..Як умовно зображаються ланки та кінематичні пари на кінематичних схемах механізмів?

6..Що називається кінематичним ланцюгом? Які є їх різновиди?

7..Дати означення простому і складному, відкритому і закритому кінематичним ланцюгам.

8. Що називається механізмом, ведучою та веденими ланками?

Лекція № 17

Тема: “Ступінь рухомості кінематичного ланцюга. Основні різновиди механізмів”

1..Визначення ступеню рухомості кінематичного ланцюга загального вигляду та плоского механізму.

2. Поняття про пасивні в’язі та зайві ступені вільності.

3. Огляд основних різновидів механізмів.

1..Визначення ступеню рухомості кінематичного ланцюга загального вигляду та плоского механізму

Кількість ступенів вільності кінематичного ланцюга відносно ланки, обраної за нерухому, називається кількість ступенів рухомості або просто ступенем рухомості кінематичного ланцюга.

Ступінь рухомості кінематичного ланцюга загального вигляду (просторового механізму) визначається за формулою:

W=6n–5p₅ – 4p₄ – 3p₃ – 2p₂ – p₁,

де n – кількість рухомих ланок кінематичного ланцюга; p₅, p₄, p₃, p₂, p₁ – кількість кінематичних пар відповідно п’ятого, четвертого, третього, другого і першого класів.

Ця формула носить назву формули Сомова-Малишева (за прізвищами вчених, що її довели: в 1887р. – П.І. Сомов, у 1923р. – О.П. Малишев) або формули рухомості, структурної формули кінематичного ланцюга загального вигляду.

Для плоских механізмів структурна формула має вигляд:

W=(6–3)n–(5–3)p₅–(4–3)p₄–(3–3)p₃,

оскільки в площині на рух всіх ланок накладено 3 спільні обмеження.

Таким чином, ступінь рухомості плоского механізму визначається за формулою:

W=3n–2p₅ – p₄.

Ця формула вперше була виведена П.Л.Чебишовим у 1869р. і тому носить назву формули Чебишова.

Ступінь рухомості механізму визначається кількістю ведучих ланок, закони руху яких задані.

Розглянемо приклад. Необхідно визначити ступінь рухомості механізму, зображеного на рис.1.

У цьому механізмі кількість рухомих ланок дорівнює 5 (n=5), а кількість кінематичних пар п’ятого класу дорівнює 7 (p₅=7), пар четвертого класу немає, тоді:

W=3n–2p₅–p₄=3·5–2·7–0=1.

Рис.1

Отже, достатньо одній ланці задати рух, щоб рухи решти ланок були однозначно визначальними.

2. Поняття про пасивні в’язі та зайві ступені вільності

Слід відзначити, що крім тих в’язей, які активно впливають на характер руху ланок у механізмі, в них можуть зустрічатися такі ступені вільності й в’язі, які ніяк не впливають на характер руху механізму в цілому. Такі ступені вільності називаються зайвими, а в’язі – пасивними або надлишковими.

Нехай маємо механізм, зображений на рис.2.

Рис.2

Підрахуємо його ступінь рухомості. Оскільки n=4, p₅=6, p₄=0, то:

W=3n–2p₅–p₄=3·4–2·6=0.

Це, звичайно, неправильно. Рухомість цього кінематичного ланцюга дорівнює одиниці. Очевидно, отриманий результат (W=0) справедливий лише для системи з ланкою СD, яка не паралельна і не дорівнює двом іншим ланкам АВ і О₁О₂.

Таким чином проміжна ланка СD не накладає ніяких додаткових в’язей на дану систему. Тому такі в’язі і називаються пасивними. Їх поява в механізмі обумовлена найчастіше міркуваннями конструктивного характеру. Щоб уникнути помилок, їх необхідно виявляти і вилучати із розрахунків.

Виявити пасивні в’язі в механізмі можна найпростіше у процесі вивчення їх кінематики, наприклад, при визначенні переміщень і швидкостей ведених ланок. Якщо їх можна визначити без участі однієї або декількох ланок, то останні вносять пасивні в’язі в механізм.

4. Огляд основних різновидів механізмів

Шарнірно-важільним (важільним) називається механізм, ланки якого утворюють тільки обертальні й поступальні кінематичні пари (рис.3).

Ланка шарнірно-важільного механізму, яка може здійснювати повний оберт навколо нерухомої осі називається кривошипом (ланка 1).

Ланка шарнірно-важільного механізму, яка не утворює кінематичної пари зі стояком називається шатуном (ланка 4).

Ланка важільного механізму, яка утворює поступальну пару зі стояком, називається повзуном (ланка 5).

Рис.3

Ланка важільного механізму, яка обертається навколо нерухомої осі й утворює з іншою рухомою ланкою поступальну пару, називається кулісою (ланка 3).

Важільний механізм, до складу якого входить куліса, називається кулісним (рис.3).

Шарнірно-важільний механізм, ланки якого утворюють тільки обертальні пари, називають шарнірним механізмом (рис.4).

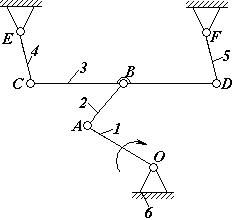
Рис.4

Ланка шарнірно-важільного механізму, яка може здійснювати тільки неповний оберт навколо нерухомої осі, називається коромислом (ланки 4, 5).

Шарнірний механізм, до складу якого входять три рухомі ланки, називається шарнірним чотириланковиком (рис.5).

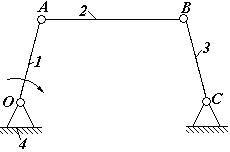
Рис.5

Шарнірно-важільний чотириланковий механізм, до складу якого входить кривошип і повзун, називають кривошипно-повзунковим або кривошипно-шатунним (рис.6).

Рис.6

Кулачковим називають механізм, до складу якого входить кулачок, тобто така ланка, елемент якої має змінну кривизну (рис.7).

Ланка 1, яка утворює з кулачком кінематичну пару, називається штовхачем.

Зубчатим називається механізм, до складу якого входять зубчаті колеса.

Фрикційним називається механізм, в якому для передачі руху використовують силу тертя.

Розрізняють механізми з гнучкими ланками, які в залежності від вигляду гнучкої ланки називаються пасовою, ланцюговою або канатною передачами.

Комбінованим називається механізм, що складається з двох або більше механізмів різних видів (так, якщо в механізм входить кулачок і зубчате колесо, то він називається кулачково-зубчатим).

Всі перелічені вище механізми будуть розглядатися в процесі подальшого викладення матеріалу.

Питання для самоконтролю

1..Як визначається ступінь рухомості просторового кінематичного ланцюга, плоского механізму?

2..Які в’язі називаються пасивними? Чим обумовлена їх поява в механізмі? Як їх виявити?

3..Який механізм називається шарнірно-важільним (важільним), кулісним, шарнірним?

4..Дати означення кривошипу, шатуну, повзуну, кулісі, коромислу.

5..Які механізми відносяться до найпростіших важільних? Дати їм означення.

6..Дати означення кулачковим, фрикційним, зубчатим, комбінованим механізмам, а також механізмам з гнучкими ланками.

Лекція №18

Тема: “Групи Ассура. Основний принцип утворення механізмів”

1. Заміна вищих кінематичних пар у плоскому механізмі нижчими.

2. Групи Ассура та їх класифікація.

3. Основний принцип утворення механізмів.

4. Приклад структурного аналізу механізму.

1. Заміна вищих кінематичних пар у плоскому механізмі нижчими

У процесі вивчення структури і кінематики плоских механізмів часто зручно заміняти вищі кінематичні пари на нижчі. При цьому повинні виконуватись дві умови:

Рис.1

1) щоб механізм, який дістали після заміни, мав такий же ступінь рухомості, як і до заміни;

2) щоб збереглись відносні рухи всіх ланок у цьому положенні.

Розглянемо механізм, зображений на рис.1.

Він складається з двох рухомих ланок 2 та 3, які входять в обертальні кінематичні пари п’ятого класу А та В зі стояком 1 і вищу кінематичну пару С четвертого класу, елементи ланок якої є колами радіусів.

За формулою Чебишова ступінь рухомості такого механізму дорівнює:

W=3n–2p₅–p₄=3·2–2·2–1=1.

Замінимо цей механізм еквівалентним йому АО₂О₃В. Вища пара заміняється ланкою 4, яка утворює в точках О₂ і О₃ обертальні пари п’ятого класу. Отриманий у результаті заміни механізм АО₂О₃В називають замінним механізмом.

Ступінь рухомості замінного механізму буде таким же, що і вихідного:

W=3n–2p₅–p₄=3·3–2·4–0=1.

2. Групи Ассура та їх класифікація

Групою Ассура називається кінематичний ланцюг, який після приєднання його до стояка має нульовий ступінь рухомості.

Якщо таку групу приєднати до рухомих ланок механізму, то ланки групи також набувають рухомості відносно одна одної, не змінюючи при цьому ступеню рухомості механізму в цілому. Із означення виходить:

W=3n–2p₅=0.

Якщо в механізмі є вищі пари, то попередньо заміняємо їх на нижчі.

Звідси: 3n-2p₅=0 або .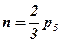

Отже, групи Ассура можуть мати тільки парну кількість ланок, а кількість кінематичних пар повинна бути кратною 3, тобто:

n=2, p₅=3; n=4, p₅=6; n=6, p₅=9; ….

Групи Ассура поділяються на класи, а кожен клас – на порядки.

За акад. І.І. Артоболевським, клас групи визначається кількістю кінематичних пар у замкнутому контурі, який входить до складу групи Ассура (рис.2).

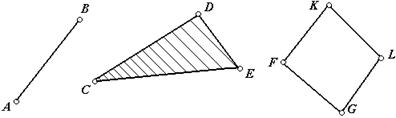
II кл. III кл. IV кл.

Рис.2

Порядок визначається кількістю зовнішніх кінематичних пар або кількістю вільних елементів групи Ассура (рис.3).

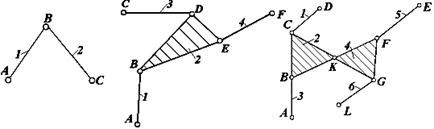
II пор IІI пор IV пор.

Рис.3

Клас і порядок механізму в цілому визначається найвищим класом і найбільшим порядком групи найвищого класу.

3. Основний принцип утворення механізмів

Основний принцип утворення механізмів був вперше сформульований у 1914р. російським вченим Л.В.Ассуром. Ним запропонований метод утворення механізмів шляхом послідовного приєднання кінематичних ланцюгів, наділених певними структурними властивостями.

Цей метод легко можна прослідкувати на конкретному прикладі. Нехай маємо механізм, зображений на рис.4.

До складу цього механізму входить п’ять рухомих ланок, які утворюють сім кінематичних пар п’ятого класу. Тому за формулою Чебишова ступінь рухомості механізму дорівнює:

W=3n–2p₅–p₄=3·5–2·7–0=1.

Рис.4

Процес утворення цього механізму можна подати як послідовне приєднання до ведучої ланки 1 і стояка 2, які утворюють ведучу групу, групи Ассура АВD, що складається із ланок 2 та 3. Тоді дістанемо чотириланковий механізм ОАВD, який має один ступінь рухомості. Далі приєднаємо групу Ассура CEF, яка складається із ланок 4 та 5,і дістанемо шестиланковий механізм, що має також ступінь рухомості одиницю.

Тепер неважко встановити певну закономірність процесу утворення механізму.

Будь-який механізм має одну нерухому ланку (стояк). Механізм повинен мати кількість ведучих ланок, яка б відповідала кількості ступенів рухомості. У даному випадку одна ведуча ланка, оскільки ступінь рухомості механізму дорівнює 1.

Через те, що після приєднання ведених ланок 2, 3, 4 і 5 ступінь рухомості всього механізму залишається рівним 1, то кінематичний ланцюг, до складу якого входять ланки 2, 3, 4 і 5, приєднаний до ведучої групи, має нульовий ступінь рухомості відносно тих ланок, до яких він приєднаний.

Ведуча ланка зі стояком утворюють ведучу групу І класу.

Формула, що характеризує послідовність приєднання груп Ассура до ведучої групи, називається формулою будови механізму.

Для даного механізму вона має вигляд:

ІкІп ÞІІкІІп(2,3) ÞІІкІІп (4, 5).

Завершивши вивчення теми “Структура та класифікація механізмів і машин” зробимо висновок: структурний аналіз механізму включає в себе визначення кількості ланок, кількості й класу кінематичних пар, які утворюють цей механізм, обчислення ступеню рухомості, розділення його на групи Ассура, а також встановлення класу і порядку груп Ассура та механізму в цілому.

4. Приклад структурного аналізу механізму

1. Зображений на рис.5 механізм – плоский, шарнірно-важільний.

2. Масштаб побудови обчислюється за формулою:

.

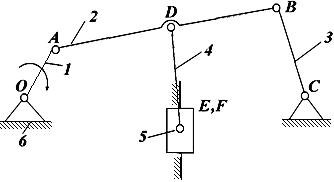
Рис.5

3. Таблиця кінематичних пар:

Позначення пари		А	В	С	D	E	F
Ланки, що її утворюють	1,6	1,2	2,3	3,6	2,4	4,5	5,6
Клас

4. Ступінь рухомості механізму:

W=3n–2p₅–p₄=3·5–2·7–0=1.

Отже, цей механізм має одну ведучу ланку, тобто одній ланці слід задати рух, щоб решта виконувала однозначно визначальні рухи.

5. Розділення механізму на групи Ассура:

ведуча група г р у п и А с с у р а

6. У цілому механізм ІІ класу ІІ порядку.

7. Формула будови механізму:

ІкІп®ІІкІІп(2, 3)®ІІкІІп(4, 5).

Питання для самоконтролю

1. Які умови повинні виконуватися при заміні вищої пари нижчими?

2. Що називається групою Ассура? Скільки ланок та кінематичних пар утворюють групу Ассура?

3. Як класифікуються групи Ассура?

4. Сформулювати принцип утворення механізмів.

5. У чому полягає структурний аналіз механізмів?

Лекція № 19

Тема: “Кінематичний аналіз шарнірно-важільних механізмів. Побудова плану швидкостей”

1..Завдання та методи кінематичного дослідження механізмів.

2..Побудова положень і траєкторій окремих точок ланок механізму.

3..Кінематичний аналіз механізмів методом планів швидкостей і прискорень. Побудова плану швидкостей.

1..Завдання та методи кінематичного дослідження механізмів

Кінематичний аналіз механізмів полягає у вивченні рухів ланок механізмів за заданим рухом ведучих ланок без врахування сил, що діють на них.

Основні завдання:

1. Визначення положень ланок, включаючи і визначення траєкторій окремих точок ланок механізму.

2. Визначення швидкостей та прискорень точок та кутових швидкостей і прискорень ланок механізму.

Вихідними даними для кінематичного дослідження є закон руху ведучої ланки (ланок) і кінематична схема механізму.

Існують такі методи кінематичного аналізу:

1) графічно-аналітичний:

а) метод планів швидкостей і прискорень;

б) метод побудови кінематичних діаграм (графічного диференціювання);

2) аналітичний;

3) експериментальний.

2..Побудова положень і траєкторій окремих точок ланок механізму

Крива, по якій переміщається точка ланки під час роботи механізму, називається траєкторією цієї точки.

Існують такі методи побудови траєкторій:

а) засічок;

б) шаблонів;

в) моделей.

Розглянемо метод засічок на прикладі кривошипно–повзункового механізму (рис.1).

Рис.1

Перш ніж знаходити траєкторії окремих точок, необхідно побудувати механізм у масштабі. Вихідні дані:кінематична схема і розміри ланок.

Цей механізм ІІ класу ІІ порядку.

Положення ланок механізму креслимо в наступній послідовності. Спочатку наносяться всі нерухомі елементи (центри нерухомих шарнірів і осі напрямних поступальних пар), потім креслиться ведуча ланка, після чого перша група Ассура (причому спочатку визначаються положення зовнішніх точок, а потім – внутрішньої), потім друга, третя і всі інші групи. Якщо дві групи Ассура приєднані паралельно, то першою можна креслити будь-яку з них.

Побудуємо цю кінематичну схему в масштабі .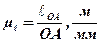

Для цього у довільному місці помічаємо точку О, вправо від неї проводимо горизонтальну пряму – вісь напрямної поступальної пари (геометричне місце точок В). Таким чином, всі нерухомі елементи нанесені.

Потім креслимо кривошип. Він обертається і в різні моменти часу займає різні положення. Перше положення кривошипа обирають довільно. Відкладемо від точки О вертикально вгору довжину кривошипа ОА (в масштабі). Зовнішні пари вже нанесені: А – кінець кривошипа, С – нерухома точка, що лежить на осі х-х. Положення точки В знаходимо засічкою. Для цього розміром АВ із точки А, як із центра, на прямій х-х робимо засічку. З’єднавши відрізком прямої точки А і В, дістанемо перше положення групи Ассура. Щоб побудувати друге положення механізму, повернемо кривошип на 30°і знайдемо положення всіх зазначених вище точок.

Потім побудуємо траєкторію точки D. Для цього із точки А, як із центра, в кожному положенні механізму роблять засічки розміром АD і сполучають отримані точки плавною кривою.

3. Кінематичний аналіз механізму методом планів швидкостей і прискорень. Побудова плану швидкостей

Планом швидкостей (прискорень) ланки називається графічна побудова у вигляді плоского пучка, промені якого зображають абсолютні швидкості (прискорення) точок ланки плоского механізму, а відрізки, що сполучають кінці променів, – відносні швидкості (прискорення) відповідних точок у даному положенні ланки.

Планом швидкостей (прискорень) механізму називається сукупність планів швидкостей (прискорень) ланок механізму з одним спільним полюсом.

Розглянемо цей метод на прикладі групи Ассура ІІ класу (рис.2,а).

Вихідні дані: вектори швидкостей точок В і D кінцевих елементів групи (відкритих кінематичних пар) та кінематична схема групи. Необхідно визначити вектор швидкості точки С.

Рух точки С може бути розкладений на переносно-поступальний зі швидкістю точки В або точки D і відносно-обертальний відповідно відносно точки В або точки D.

а)

б)

Рис.2

Тоді векторні рівняння для точки С будуть мати вигляд:

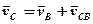; (1)

. (2)

Прирівняємо праві частини рівнянь:

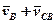
. (3)

У рівнянні (3) відомі за величиною і напрямком вектори швидкостей і . Вектори ж швидкостей і відомі тільки за напрямком: вектор обертальної швидкості точки С відносно точки В напрямлений перпендикулярно до ланки ВС, а вектор швидкості точки С відносно точки D напрямлений перпендикулярно до сторони СD ланки 3.

Таким чином, у рівнянні (3) невідомі тільки величини векторів швидкостей 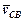і , які можуть бути визначені побудовою плану швидкостей (рис.2,б).

Для цього обираємо за полюс плану швидкостей довільну точку р і відкладаємо від неї відрізок рb, який зображає швидкість точки b в обраному масштабі:

.

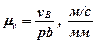При виборі величини масштабу μ_v керуються зручністю обчислень і побудови векторів швидкостей.

Відклавши відрізок рb, проведемо через точку b пряму, перпендикулярно до ланки ВС (напрямок обертальної швидкості ).

Далі з полюса р проведемо відрізок pd, який відповідає швидкості в обраному масштабі, і через кінець цього вектора d проведемо напрямок вектора відносної швидкості перпендикулярно до ланки СD.

Швидкість точки С визначається відрізком, що сполучає полюс р з отриманою точкою с.

Її дійсне значення:

v_C=(pc) μ_v.

Відрізки bc і dc виражають відносні швидкості і у тому ж масштабі:

v_CВ=(cb) μ_v,

v_CD=(cd) μ_v.

Напрямок векторів проставляємо відповідно до рівняння (3).

Трикутники рвс і pdc називають планами швидкостей ланок, а фігура pbcd називається планом швидкостей групи ВСD. Точка p – полюс плану швидкостей.

Користуючись планом швидкостей, можна визначити кутові швидкості ω₁ і ω₂ ланок 2 і 3.

Величини цих швидкостей визначаються за формулами:

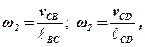
де 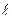_BC, 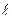_CD – дійсні довжини ланок ВC і СD.

Підставляючи в рівняння величини швидкостей 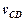і 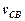, дістанемо:

Напрямок кутових швидкостей ω₂ та ω₃ можуть бути визначені таким чином. Подумки прикладаємо відрізки bc і dc, що зображають вектори і , до точки С кінематичної схеми, і бачимо, що обертання ланки 2 відбувається в напрямку ходу годинникової стрілки, а обертання ланки 3 – в напрямку, зворотному ходу годинникової стрілки.

Для визначення швидкості будь-якої точки F, яка лежить на осі ланки ВС, маємо векторне рівняння:

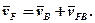
Згідно цього рівняння із точки b плану швидкостей проводимо напрямок вектора відносної швидкості точки F навколо точки В. Оскільки відносні швидкості будь-яких точок, що лежать на осі ВС ланки 2, перпендикулярні до осі ВС, то напрямок збігається з напрямком , тобто напрямок відрізка плану швидкостей bf збігаються з напрямком з відрізка bc.

Величину швидкості 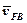визначаємо із рівнянь:

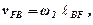
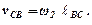
Розділивши почленно першу рівність на другу, дістанемо:

.

Із рівняння випливає, що швидкості точок F та C відносно точки В прямо пропорційні відстаням цих точок до точки В.

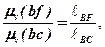
звідки:

Таким чином, щоб визначити відрізок плану швидкостей, який зображає відносну швидкість , необхідно відрізок bc, який зображений на плані швидкостей відносну швидкість 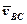, розділити у тому ж співвідношенні, в якому точка F ділить ланку 2 на схемі групи. Відклавши отриманий відрізок на плані швидкостей і сполучивши точку f з полюсом р, дістанемо швидкість :

v_F=(pf)·μ_v.

Для визначення швидкості якої-небудь довільної точки Е ланки 3, складемо такі векторні рівняння:

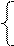
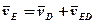, (4)

. (5)

Із рівностей дістанемо:

. (6)

Вектори і у рівнянні (6) відомі за величиною і напрямком, а вектори і 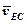відомі тільки за напрямком. Вони перпендикулярні до відрізків DЕ і ЕС. Із точки d плану швидкостей проводимо пряму, перпендикулярну до DЕ, а через точку с – перпендикулярну стороні ЕС. Точка перетину е і визначить кінець вектора швидкості :

v_Е=(pе)·μ_v.

Розглядаючи трикутник cdе плану швидкостей і трикутник CDЕ на ланці можна бачити, що відрізки се, еd та dc відповідно перпендикулярні до відрізків CE, DЕ та DC, тобто: ,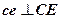

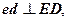
Таким чином, трикутник сdе на плані швидкостей подібний трикутнику СDЕ групи Ассура на кінематичній схемі й повернутий відносно нього на кут 90°. Ця властивість подібності дозволяє визначати швидкості будь-яких точок ланок механізму графічно, побудовою подібних фігур.

Питання для самоконтролю

1. У чому полягає кінематичний аналіз механізмів? Які завдання він виконує?

2. Які вихідні дані необхідні для кінематичного дослідження механізму і які його методи?

3. Які існують методи побудови положень ланок та траєкторій їх точок? Сутність методу засічок.

4. Дати означення плану швидкостей (прискорень) ланки та механізму.

5. Які вихідні дані мають бути при побудові плану швидкостей групи Ассура ІІ класу?

6. Як визначається швидкість точки ланки механізму, яка здійснює плоскопаралельний рух?

7. Як визначається величина та напрямок швидкості точки ланки, що здійснює обертальний рух?

8. Як визначаються кутові швидкості обертання ланок механізму (величина та напрямок)?

9. Як визначаються дійсні швидкості точок ланок механізму із плану швидкостей?

10. Визначення швидкості точки ланки, яка лежить на її осі.

11. Визначення швидкості точки ланки, яка не лежить на її осі.

12. Послідовність побудови плану швидкостей.

Лекція № 20

Тема: “ Кінематичний аналіз шарнірно-важільних механізмів. Побудова плану прискорень”

2..Приклад кінематичного аналізу плоского механізму методом планів.

Дата добавления: 2014-10-23