Понятие об идентификации

Математические модели широко применяются для анализа работы технологических объектов с целью отыскания наиболее благоприятных режимов с точки зрения экономики и безопасности. Связано это с практически бесконечными возможностями испытания математической модели на ЭВМ, что обусловлено рядом факторов.

Во-первых, моделирование основано на ограниченности числа фундаментальных законов природы и принципе подобия, означающем, что явления различной физической природы могут описываться одинаковыми математическими зависимостями.

Во-вторых, экспериментирование на реальных объектах обычно ограничивается факторами экономического характера (стоимостью измерительных приборов, затратами труда, возможностью получения бракованного продукта и пр.), в то время как эксперименты на ЭВМ не требуют обычно больших затрат и полностью безопасны.

В-третьих, численные эксперименты, проводимые на вычислительных машинах, точно воспроизводимы, поэтому неожиданные результаты можно проверить и установить их причину, повторяя эксперименты в неизменных условиях.

Объекты моделирования (и управления) обычно классифицируют как:

• статические или динамические;

• линейные или нелинейные;

• непрерывные или дискретные;

• стационарные или нестационарные;

• с сосредоточенными или распределенными параметрами.

Под моделью обычно понимается информация о наиболее существенных характеристиках объекта, выраженная в той или иной форме. По способу представления информации выделяют следующие типы моделей:

• словесные или вербальные;

• физические (уменьшенные копии реальных объектов или объектов иной физической природы, позволяющие имитировать процессы в исследуемом объекте);

• математические (информация об исследуемом объекте или системе представляется в виде математических терминов);

• формальные (основанные на формальной аналогии с описываемыми объектами).

В свою очередь, математические модели делятся на графические, табличные, топологические, алгоритмические и аналитические. В частности, аналитические модели представляют собой отражение взаимосвязей между переменными объекта в виде одной или группы математических формул.

Процедуру построения модели принято называть идентификацией, при этом данный термин обычно относится к построению аналитических математических моделей динамических объектов.

Динамический объект – это объект, выход которого зависит не только от текущего значения входных сигналов, но и от их значений в предыдущие моменты времени. Идентифицируемый объект принято представлять в виде, показанном на рис. 5.1, где t – время; x(t) – контролируемый (иногда управляемый) входной сигнал; y_t(t) – теоретический выход объекта; y(t) – наблюдаемый выход объекта; e(t) – случайная аддитивная помеха, отражающая действие не учитываемых факторов (шум наблюдения).

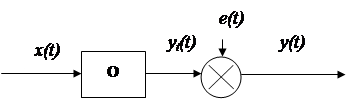Рис 5.1. Общее представление идентифицируемого объекта О

Обычно предполагают, что связь между входным и «теоретическим» выходным сигналами задается в виде некоторого оператора A_t (оператор – правило преобразования какой-либо функции в другую функцию):

y_t(t) = A_t [ x(t) ], (5.1)

при этом наблюдаемый выход объекта может быть описан соотношением

y(t) = A_t [ x(t) ] + e(t). (5.2)

Таким образом, цель идентификации - на основании наблюдений за входным x(t) и выходным y(t) сигналами на каком-то интервале времени определить вид оператора, связывающего входной и «теоретический» выходной сигналы.

Примером таких операторов могут служить операторы дифференцирования y(t) = dx/dt, интегрирования 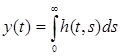, сдвига назад Dy(t) = y(t-t) и т. д. В качестве математической модели могут использоваться также алгебраические, дифференциальные и интегральные урав­нения, импульсные переходные функции, частотные характеристи­ки, оператор условного математического ожидания m_у = f(x_l,..., х_n), условная плотность распределения вероятностей j (y/ Х).

Идентификация – сложная процедура, которая содержит следующие этапы:

• структурная идентификация – определение структуры математической модели на основании теоретических соображений;

• параметрическая идентификация – проведение идентифицирующего эксперимента и определение оценок параметров модели по экспериментальным данным;

• проверка адекватности – проверка качества модели по критерию близости выходов модели и объекта.

Дата добавления: 2014-10-23