Основные характеристики (функции) систем

Решение задачи идентификации может быть основано на активных экспериментах или на результатах наблюдений за объектом в условиях нормального функционирования. При экспериментальном определении параметров модели необходимо обеспечить подбор адекватной структуры модели и выбор такого входного сигнала, с помощью которого по результатам эксперимента можно было бы найти оценки всех параметров модели.

Самые ранние методы идентификации были основаны на использовании частотных, ступенчатых и импульсных воздействий.

При ча­стотном методе воздействия на вход объекта подается синусоидальный сигнал, частота которого изменяется в рассматриваемом диапазоне. В основе метода лежит отношение преобразований Лапласа выхода Y(p)=L [ y(t) ] объекта и его входа X(p)=L [ x(t) ]

W(p) = Y (p)/X (p), (5.11)

где W(p) – передаточная функция; p =s + jw – комплексный параметр.

Поскольку интерес представляет изменение соотно­шения вход-выход по частоте, вместо выражения (5.11) можно записать Y(jw) = W(jw)Х(jw). Частотная характеристика W(jw) определяется путем подачи синусоидальных входных сиг­налов Мsin(w t) на различных частотах w и записи соответствую­щих выходных сигналов Nsin(w t - f). При построении ампли­тудной (АЧХ) и фазовой (ФЧХ) частотных характеристик определяется частотная зависимость отношения амплитуд M/N и величины сдвига фаз f.

Идентификация с помощью переходной функции h(t)=L ^-1[ H(p) ] осуществля­ется подачей на вход объекта ступенчатого сигнала. По­скольку преобразование Лапласа для ступенчатого единичного сигнала при t = 0 есть 1 /p, то переходная функция линейного объекта

H(p) = W (p)/p. (5.12)

Практически такой сигнал может быть реализован без использования специальной аппа­ратуры путем резкого изменения входного воздействия (изменение подачи реагента, закрытие или открытие клапана и т. п.).

В импульсном методе при подаче на вход линейного объекта сигнала в виде дельта-функции d(t) на его выходе получаем сигнал в виде импульсной функции g(t)=L ^-1[ G(p) ]. Преобразование Лапласа для дельта-функции имеет вид X (p) = L [ d (t) ] = 1, поэтому

G(p) = W (p). (5.13)

Таким образом, передаточ­ная функция линейного объ­екта равна преобразованию Лапласа от его импульсной переходной функции:

W(p) = L [ g (t) ], (5.14)

Отсюда, в частности, следует, что pH(p) = G (p), изначит h¢ (t) = g (t).

В практике идентификации широко применяются корреляци­онные и регрессионные методы. Идентификация с помощью методов корреляци­онных функций основана на известном для линейных объектов соотношении

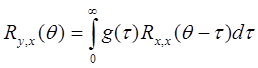, (5.15)

в котором R_y,x(q) – взаимная корреляционная функция между величиной выходного сигнала у(t) в любой момент времени t и величиной входного сигнала x (t) в момент времени t = q; R_x,x – автокор­реляционная функция входного сигнала; g (t) – импульсная реакция системы.

Если входная функция x(t) является белым шумом, тогда ее автокорреляционная функция является дельта-функцией R_x,x(q) = d(q). Взаимная корреляционная функция в этом случае при­нимает вид:

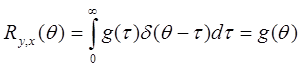. (5.16)

Заметим, что на практике входной сигнал в виде белого шума реализовать невозможно. Однако если входной сигнал имеет равномерный спектр частот (более широкий, чем спектр объекта) его автокорреляционная функция с достаточной точностью может быть аппроксимирована дельта-функцией.

Методу идентификации с помощью корреляционных функций присущи следующие достоинства:

· идентификацию можно проводить независимо от записей реализаций сигналов, получаемых в процессе нормального функционирования системы;

· вычисление корреляционных функций на достаточно большом временном интервале позволяет снизить амплитуду пробного воздействия так, чтобы объект не испытывал существенных возмущений;

· не требуется априорных сведений об идентифицируемой системе.

Применимость этого метода, однако, довольно ограничена из-за следующих недостатков:

· для решения задачи необходимо большое время;

· использование белого шума требует применения специальной аппаратуры и специальных вычислительных средств;

· метод пригоден лишь для линейных объектов с медленно меняющимися характеристиками.

Рассмотрим кратко сущность регрессионных методов идентификации. Пусть статический объект имеет m входов x ₁, …, х_m и один выход у. Регрессионной моделью объекта называется функция связи между входными и выходными сигналами в виде полиномов, как правило

линейного

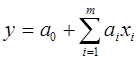, (5.17)

или квадратичного

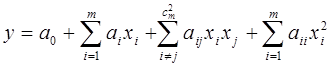, (5.17¢)

где а_ij - коэффициенты регрессии; с ²_m - число парных сочетаний из m элементов.

Поясним понятие состояния объекта. Пусть объект описывается обыкновенным дифференциальным уравнением порядка n. Любое такое уравнение можно преобразовать в систему дифференциальных уравнений первого порядка. В свою очередь система n дифференциальных уравнений первого порядка полностью определена лишь в том случае, если заданы все коэффициенты и известны n начальных условий. Эти начальные условия образуют n -мерный вектор, который полностью и точно определяет состояние объекта в момент t _о. Этот вектор называется вектором состояния системы в момент t _о, а его составляющие носят название переменных состояния. Таким образом, состояние объекта определяется вектором, который вместе с входным сигналом объекта полностью указывает его дальнейшее поведение.

При выборе n координат объекта x_i(t), i = 1, 2,..., n в качестве переменных состояния (такими координатами, например, могут быть выходной сигнал y(t) и n - 1 его производных), данный объект, на входе которого действует сигнал u(t), можно описать уравнениями для переменных состояния

Х '(t) = AX (t) + B u(t) (5.18)

y(t) = СХ (t) + Du(t),

где X (t) = [ x ₁ (t), x ₂ (t), …, x _n (t) ]^T – вектор-столбец переменных состояния; A, В, С и D – подлежащие определению при идентификации соответственно матрица размером n ´ n, векторы размером n ´1 и 1´ n, а также скаляр (при векторных u(t) и y(t) – матрицы соответствующих размеров).

Дата добавления: 2014-10-23