Математические модели многостадийных объектов

Технологические процессы (в частности, технологические процессы химического производства) реализуются обычно на совокупности технологических аппаратов, действующих как одно целое. В них осуществляется определенная последовательность технологических операций по получению целевого продукта (например, в технологических процессах химической технологии такими операциями являются подготовка сырья, смешивание, отделение примесей и т. д.).

В некоторых случаях стадии технологического процесса могут рассматриваться независимо друг от друга, каждая из них имеет свой так называемый локальный критерий. Каждая из этих стадий характеризуется определенным набором входных и управляющих воздействий, требования к выходным переменным каждой стадии могут быть четко определены. Идентификация такого многостадийного процесса сводится к построению математических моделей отдельных стадий, выбору информативных на каждой стадии переменных, подборке подходящей структуры, оценке адекватности полученных моделей.

Однако в большинстве случаев, особенно в непрерывных процессах химической технологии, стадии не могут рассматриваться как независимые. Как правило, функционирование последующей стадии зависит от протекания процесса на предыдущих стадиях; ограничения на входные, управляющие и выходные переменные стадий назначаются с учетом требований к другим стадиям, часть продуктов с выхода стадии может возвращаться на вход предыдущей стадии или в начало (голову) процесса.

Таким образом, решение задач оптимизации непрерывных многостадийных процессов предполагает обычно совместное рассмотрение отдельных технологических переделов, согласование критериев, характеризующих функционирование отдельных стадий, учет материальных и энергетических балансов всего процесса.

Отдельные технологические аппараты многостадийного процесса соединяются определенным образом, обеспечивающим более выгодное использование сырьевых ресурсов, экономное использование энергии и т. п. Основными типами соединений (связей) технологических аппаратов (элементов) химико-технологической системы (ХТС) являются последовательная, последовательно-обводная (байпac), параллельная, обратная (рецикл) и перекрестная. Все они применяются в химико-технологических системах в зависимости от характера происходящих физико-химических превращений и требований к производительности установки.

Последовательная технологическая связь обеспечивает улучшение функционирования отдельных технологических аппаратов. Она используется, например, для обеспечения более высокой степени превращения исходного сырья, повышения сте­пени разделения, степени извлечения вредных примесей и т. д.

Усложненным вариантом последовательного соединения технологических аппаратов является последовательно-обводная связь. Здесь за счет байпасирования части холодного потока сырья увеличивается концентрация реагирующих веществ на входе в последующие реакторы.

Параллельная технологическая связь при­меняется для повышения производительности технологической установки, а также при параллельном получении из одного и того же сырья двух или большего числа промежуточных продуктов, идущих на производство одного целевого продукта.

В технологи­ческих системах широко используется обратная (рециклическая) связь, когда часть потока с выхода j -го технологического аппарата подается на вход i -го аппарата. Такая связь обеспечивает более полное использование сырья, интенсивное протекание химических реакций за счет использования тепла реакции для подогрева исход­ных продуктов, наиболее полное использование катализаторов и инертных растворителей.

Наконец перекрестная технологиче­ская связь обеспечивает эффективное использование энергии хими­ко-технологической системы (например, тепло газообразных продуктов химической реакции пли отходящих газов можно ис­пользовать для предварительного нагрева сырья).

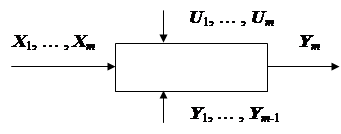Рис. 5.3. Укрупненное пред­ставление многостадийного

технологического объекта

Сложный многостадийный процесс можно рассматривать как единый блок (рис. 5.3), модель которого ищется в за­висимости выходной величины от входов и выходов всех подси­стем

Y _m = f(X ₁, …, X _m; U ₁, …, U _m; Y ₁, …, Y _{m- 1} ),(5.19)

где m – количество подсистем; X _i (i = 1, …, m) – вектор входных контролируемых переменных i -й стадии; U _i (i = 1, …, m) – вектор управляющих переменных i -й стадии; Y _j (j = 1, …, m -1) – вектор выхода j -й стадии; Y _m – критерий многостадийного технологического объекта.

В основе такого подхода к рассмотрению многостадийного технологического объекта лежит идея «черного» или «серого ящика», когда модель строится только по наблюдаемым значениям входных и выходных переменных («черный ящик») с использованием, быть может, некоторой априорной информации о механизме протекающих в объекте яв­лений («серый ящик»). Построение модели (5.19) связано с опреде­ленными сложностями.

Это, во-первых, различные динамические свойства участков, заключенных между Y _m и X _i. Различное время запаздывания требует, например, при использовании регрессионных методов для построения модели, различной частоты съема данных, различного времени для накопления выборок необходи­мого объема. Обработка экспериментального материала, если бы он и мог быть получен, тоже будет чрезвычайно громоздкой и сложной, особенно если учесть необходимость выбора наилучшей модели.

Вторая сложность, связанная с построением модели (5.19), вызывается коррелированностью переменных. Она резко увеличивает объем вычислительной работы, а иногда может сделать и принципиально невозможным построение математической модели. Следует заметить, что участкам Y _m – X ₁, Y _m – X ₂, …, Y _m – X _m на практике не удается назначить критерий оптимальности. Поэтому эти участки не могут рассматриваться как отдельные подсистемы объекта.

Таким образом, построение математической модели в виде (5.19) на основе экспериментальных данных практически едва ли выполнимо - непомерно большим становится время накопления данных, резко растут объемы необходимой экспериментальной информации, вычислительные трудности и т.п. Использование аналитических моделей при таком подходе тоже невозможно, поскольку сложный технологический процесс охватывает множество подпроцессов различной химической природы (химические реакции, процессы смешивания, разделения, тепло- и массообмена), многие из которых не имеют точного математического описания.

Таким образом, возникает задача упрощенного рассмотрения многостадийного процесса, перехода к меньшему числу перемен­ных, такой организации процедуры экспериментирования и по­строения математической модели, которая может быть выполнена экономичными и доступными средствами. Иногда такое упроще­ние может быть достигнуто за счет использования метода деком­позиции, который широко применяется в автоматическом управлении. Этот структурный метод анализа систем основан на их представле­нии в виде соединения типовых звеньев, удовлетворяющих трем четким условиям: одномерности, направленности действия, ти­повой структуре уравнения звена.

Менее строгим с математиче­ской точки зрения, но зато обоснованным с технологической точки зрения, является представление сложного многостадийного про­цесса в виде соединения типовых процессов. Конечная цель такого представления состоит в разбиении пространства переменных y ₁, …, y_q; u ₁, …, u_r; x ₁, …, y_t; f ₁, f ₂ ,..., описывающих техно­логический объект, на q подпространств более низкой размерно­сти. При этом j -е подпространство (j = 1, …, q) включает лишь те переменные, которые влияют на переменную y_j.

Пусть, напри­мер, технологический объект характеризуется переменными y ₁, y ₂, y ₃, u ₁, u ₂, x ₁, x ₂, x ₃, f ₁, f ₂, f ₃. Математическая модель такого объекта может быть представлена в виде

j _i (y ₁, y ₂, y ₃, u ₁, u ₂, x ₁, x ₂, x ₃, f ₁, f ₂, f ₃) = 0; i ³ 1. (5.20)

Предположим, что y ₁ зависит только от u ₁, x ₂, x ₃, f ₂; переменная y ₂ зависит только от y ₁, u ₁, u ₂, x ₁, x ₂; переменная y ₃ зависит только от u ₂, x ₃, f ₁, f ₂. Тогда три подпространства определяются координатами y ₁ (u ₁, x ₂, x ₃, f ₂ ); y ₂(y ₁, u ₁, u ₂, x ₁, x ₂); y ₃ (u ₂, x ₃, f ₁, f ₂). Таким образом, математиче­ская модель (5.20) может быть представлена в виде трех более про­стых блоков:

j₁(y ₁, u ₁, x ₂, x ₃, f ₂ ) = 0; j₂(y ₁, y ₂, u ₁, u ₂, x ₁, x ₂) = 0; j₂₁(y ₂, u ₁, u ₂, x ₁, x ₂, x ₃, f ₂) = 0;

j₃(y ₃, u ₂, x ₃, f ₁, f ₂) = 0. (5.21)

При этом блоки, выходные переменные которых не управляются, из модели исключаются. Если любая выходная переменная техноло­гического объекта зависит от всех остальных, то декомпозиция не­возможна. Выводы о зависимости или независимости переменных делаются на основе анализа теоретических представлений о про­цессе, результатов экспериментов и т. д.

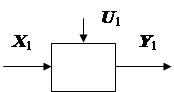
Существует несколько иной подход к построению сложных многостадий­ных технологических объектов или так называемых производ­ственных комплексов непрерывного действия (ПКН) химико-технологического профиля. Подход заклю­чается в переходе к подсистемной структуре модели (рис. 5.4). Модель комплекса имеет подсистемную структуру, если: 1) он состоит из моделей подсистем и связей между ними, причем числа подсистем m ³ 2; 2) каждой из подсистем соответствует критерий оптимальности в отличие от критерия всего процесса.

		…

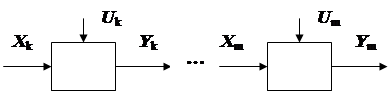Рис. 5.4. Подсистемная структура модели многостадийного

техно­логического процесса

Подсистемой может служить реактор, реакционное отделение, процесс, установка и т. д. Построение математической модели ком­плекса проходит два основных этапа: определение структуры мо­дели – формирование функциональных и позиционных ограниче­ний, выбор качественного вида модели (линейные или нелиней­ные полиномы, дифференциальные уравнения и т. д.), расчет чис­ловых значений коэффициентов ограничений.

В настоящее время предложены и детально исследованы наиболее ха­рактерные типовые структуры подсистем, которые составляют основу модели всего объекта. Это могут быть структуры сле­дующих видов:

1) статическая модель с постоянными относительными выходами;

2) статическая модель с переменными относительными выходами;

3) модель динамики с постоянными относительными выходами;

4) модель динамики с переменными относительными выходами;

5) модель для оптимизации выбора технологических вариантов работы в статике и динамике.

Связь отдельных подсистем обеспечивается за счет покомпо­нентного описания материальных потоков, связывающих отдель­ные подсистемы, применения относительных выходов компонен­тов в качестве выходных переменных и т. д.

В общем случае модель сложного многостадийного технологи­ческого процесса представляется системой нелинейных алгебраических или дифференциальных уравнений большой размерности, дополненной системой позиционных и функциональных ограничений. Так, например, система уравнений материальных и тепловых балансов химико-технологического процесса производства карбамида по схеме с полным жидкостным рециклом состоит из N >100 балансовых уравнений и М > 150 уравнений связи входных и выходных переменных. Модель производства серной кислоты имет около 500 информа­ционных связей, из которых более половины нелинейны.

Громозд­кость и сложность получаемых математических моделей требует особой тщательности при выборе информативных переменных, включаемых в модель. Особенно ответственным является вопрос о согласовании критериев отдельных подсистем (локальных критериев) с общим (глобальным) критерием процесса. Иногда эта задача сводится к согласованию допусков на выходные переменные отдельных подсистем с допусками на общий выход процесса. Решение этих задач зависит от особенностей конкретного технологического объекта.

Глава 6. ОПТИМИЗАЦИЯ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ

Дата добавления: 2014-10-23