Свойства симметрических матриц

Задача о собственных значениях

Ограничимся в рассуждениях ЛП размерности 3, евклидовым, с ортонормированным базисом (е₁ е₂ е₃). Договоримся вектором (элементом ЛП) называть матрицу-столбец = (х₁ х₂ х₃)^T. Как уже известно, умножение квадратной матрицы А на вектор дает матрицу-столбец – новый вектор из того же ЛП.

Определение. Ненулевой называют собственным вектором оператора А (матрицы А), если выполняется равенство А=к, где к – некоторое действительное, которое называют собственным значением оператора А (матрицы А).

Равенство А=к эквивалентно равенству (А-кЕ) =0, которое после выполнения действий слева фактически будет иметь вид однородной системы линейных уравнений. Однородная система имеет ненулевые (нетривиальные) решения, только если ее определитель равен нулю. (См раздел 1.5). Получаем det(A-kE)=0 или для размерности 3

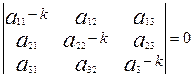(1)

Последнее уравнение с неизвестным к называют характеристическим уравнением. Решив уравнение (1.10.1) мы получим собственные значения оператора А (матрицы А). Теперь поступаем так. Берем первое собственное значение и подставляем его в систему (А-кЕ) =0 с неизвестными координатами вектора . Определителем этой системы будет определитель из леовй части уравнения (1.10.1) при заданном к. Решаем эту систему по известному алгоритмы из раздела 1.5. Получаем координаты первого собственного вектора. Далее процесс повторяется для оставшихся собственных значений.

Пример. Найдите собственные значения и собственные векторы оператора (матрицы) А=. Решение. Уравнение имеет вид

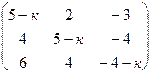=0.

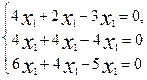Или к³-6к²+11к-6=0. Его решения (корни): к₁=1; к₂=2; к₃=3. Берем к₁=1 и составляем систему с неизвестными координатами первого собственного вектора ₁. Получаем систему . По алгоритму раздела 1.5 ранг матрицы этой системы не меньше 1 (т.к. есть элементы, не равные нулю) и не больше 3 (т.к. определитель системы это левая часть характеристического уравнения). И потому rancA=2. Легко видеть, что базисным минором может служить минор 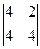=8, не равный нулю. Отбрасываем третье уравнение. Положим неизвестное х₃=2 (или любому другому не равному нулю числу) и после решения системы 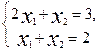получаем первый собственный вектор ₁=(1 1 2)^T. Аналогичным образом находим остальные собственные векторы: ₂=(1 0 1)^T для собственного значения к=2 и ₃=(1 2 2)^T для собственного значения к=3.

Комментарии. Как видим, сама задача распадается на три отдельные крупные математические задачи. Первая – составление характеристического уравнения. Записать определитель достаточно просто, но вычислять его при большой размерности очень трудно. Вторая – поиск решений (корней) уже полученного уравнения – одна из труднейших задач математики. В данном случае использована теорема о том, что корнями полинома с целыми коэффициентами могут быть делители свободного члена. И третья задача – поиск ненулевого решения однородной линейной системы.

Однако решать задачу нужно, т.к. она является базовой в приложениях при исследовании устойчивости линейных систем (не обязательно математических, но и систем передачи переменных напряжений от источника к потребителю).

Определение. Матрицу называют симметрической, если a_ij=a_ji. Для всех i,j.

Теорема. Собственные значения симметрической матрицы – действительные числа, собственные векторы – ортогональны.

Доказательство. Ограничимся матрицей размерности 2. Имеем А=.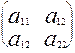

Характеристическое уравнение имеет вид к²-(а₁₁+а₂₂)+(а₁₁а₂₂-а₁₂²)=0. Его дискриминант равен (а₁₁+а₂₂)²-4(а₁₁а₂₂-а₁₂²)= (а₁₁-а₂₂)²+4а₁₂²0. А это значит – корни квадратного уравнения действительные числа.

Рассмотрим случай разных корней. Тогда по Виету имеем к₁+к₂= а₁₁+а₂₂, и к₁к₂= а₁₁а₂₂-а₁₂² .С другой стороны для к₁ найдем собственный вектор ₁ из системы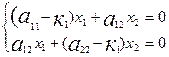

Как известно, в этой системе одно из уравнений лишнее, т.к. r(A)=1. И потому мы отбросим, например, второе уравнение в системе и возьмем х₂=а₁₁-к₁. Тогда получим собственный вектор ₁=(-а₁₂ а₁₁-к₁)^T. Из аналогичных рассуждений найдем ₂=(-а₁₂ а₁₁-к₂)^T. Теперь вычислим их скалярное произведение ₁₂=а₁₂²+(а₁₁-к₁)(а₁₁-к₂)= а₁₂²+а₁₁²- а₁₁(а₁₁+ а₂₂)+ а₁₁а₂₂-а₁₂² =0.

Если же корни равны, то это происходит только тогда, когда одновременно а₁₂=0 и а₁₁- а₂₂=0. Но это может быть только если к₁= к₂ = а₁₁. Но тогда в качестве ₁ можно взять ₁=(1 0)^T,а в качестве ₂ можно взять ₂=(0 1)^T . И все равно они будут ортогональны.

Дата добавления: 2014-10-23