Матричный метод решения линейной системы

Определение. Матрицу А^-1 называют обратной для матрицы А, если А^-1 А=А А^-1 =Е.

Из определения следует, что матрицы А и А^-1 квадратные и для них справедлив переместительный закон.

Теорема. Если А невырождена, то обратная матрица существует.

Доказательство. Ограничимся квадратной матрицей 2-го порядка.

Пусть имеется некоторая матрица А=.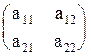

Пусть detA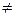0. Пусть имеется некоторая матрица В=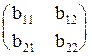- неизвестная нам. И пусть АВ=Е, где Е=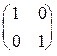. Тогда после умножения слева по равенству матриц получаем систему 4-х уравнений с четырьмя неизвестными элементами матрицы В: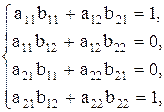, которая фактически распадается на две автономные системы, каждая из которых имеет один и тот же определитель, равный 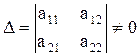определителю матрицы А и только по две переменные.: 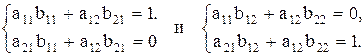Каждую из этих систем можно решить, например, по формулам Крамера и получить ответ в виде: 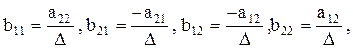в числителях каждой дроби записано алгебраическое дополнение соответствующих элементов транспонированной матрицы А^Т. Доказательство закончено. И из него вытекает алгоритм поиска А^-1:

1-й шаг - вычисли detA;

2-й шаг - если detA не равен нулю, перейдите к пункту 3, иначе обратной матрицы не существует;

3-й шаг - транспонируйте матрицу А;

4-й шаг - для всех элементов транспонированной матрицы выпишите алгебраические дополнения;

5-й шаг составьте обратную матрицу из отношений .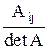

Используя обратную матрицу легко решить линейную систему, если она имеет единственное решение. В самом деле, пусть дана система АХ=В с невырожденной матрицей А (т.е. detA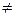0). Сформируем матрицу А^-1 по вышеприведенному алгоритму. Теперь умножим слева обе части уравнение АХ=В на матрицу А^-1. Получим А^-1АХ= А^-1 В. Но А^-1 А=Е, а ЕХ=Х и потому получаем Х= А^-1В.

Пример 1.6. Решите систему

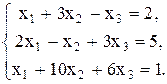
Ранг основной и расширенной матрицы этой системы равен 2 и потому система имеет решение. Базисный минор системы равен М₂ и приведен в примере 5. Фактически нам предстоит решить систему .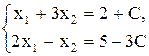

На этот раз мы решим ее, используя обратную матрицу для последней системы. Так как матрица последней системы невырождена (detA= М₂), легко найти ее обратную матрицу А^-1 =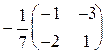, а потому решение принимает вид Х= =.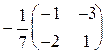

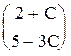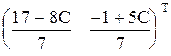А для исходной системы Х=.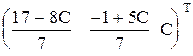

Ответ: система имеет бесчисленное количество решений, определяемых по формуле для Х.

Дата добавления: 2014-10-23