Понятие о приближенных методах решения линейных систем

Рассмотренные примеры решения линейных систем являются чисто учебными. На практике (при решении прикладных профессиональных или научных задач) приходится решать системы с сотнями, тысячами и даже сотнями тысяч уравнений. Естественно, что выполнить это можно только специальными численными методами. Понятие о некоторых из них и рассматривается в этом разделе. Сразу следует отметить, что эти методы обеспечивают поиск только единственно существующего решения системы. Вопросы обеспечения наличия или отсутствия решения решает тот, кто собирается решать такую систему.

Для линейных систем с несколькими сотнями уравнений используют метод Гаусса (метод последовательного исключения неизвестных в разных вариациях). Для систем с несколькими тысячами уравнений, матрицы которых имеют специальный вид, используют итерационные методы решения(о которых будет сказано ниже). Для большего числа уравнений используют вероятностные методы Монте-Карло).

Пусть систему АХ+В удалось преобразовать к виду Х= А₁Х+В₁. Если матрица А₁ такова, что:

- сумма модулей коэффициентов строки (для всех строк) не превосходит 1;

- сумма модулей коэффициентов столбца (для всех столбцов) не превосходит 1, тогда можно организовать вычислительный процесс по схеме Х^(k+1)= А₁Х^(k) +В₁, где k - номер предыдущего приближения к решению системы. Этот процесс называют итерационным (повторяющимся) и продолжают до тех пор, пока 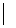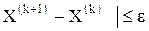, где 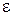- требуемая погрешность решения задачи. В качестве приближенного решения системы берут матрицу-столбец Х^(k+1).

Пример 1.7. Методом итераций решить систему

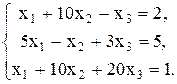
Решение. переставим в системе первое и второе уравнение. Затем из первого уравнения найдем х₁; из второго - х₂ и из третьего х₃. В результате получим систему вида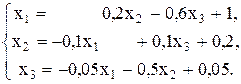

Теперь организуем итерационный процесс по схеме

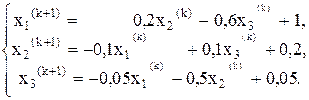
Проверяем выполнение условий сходимости процесса к точному решению системы. Видим,что сумма модулей коэффициентов при неизвестных в 1-й строке равна 0,8, что меньше 1. То же самое верно для

2-й и 3-й строк. Т.о. система обеспечивает сходимость приближений к точному решению.

В эту итерационную схему в качестве нулевого (k=0) приближения в правую часть подставим столбец свободных членов (так чаще всего и делают, хотя можно было брать любой набор для неизвестных)

Х^(о) = (1 0,2 0,05) ^Т.Тогда после вычислений справа получим слева первое (k=1) приближение Х⁽¹⁾ = (1,01 0,105 -0,1) ^Т. Повторим вычисления и получим последовательно Х⁽²⁾ = (1,081 0,089 -0,053) ^Т ;

Х⁽³⁾ = (1,050 0,087 -0,048) ^Т; Х⁽⁴⁾ = (1,046 0,090 -0,046) ^Т;

Х⁽⁵⁾ = (1,046 0,090 -0,047) ^Т; Х⁽⁶⁾ = (1,046 0,090 -0,048) ^Т. Мы видим, Что между 6-м и 5-м приближениями расхождение не превосходит 0,001. Поэтому в качестве решения системы может быть принято шестое приближение Х= Х⁽⁶⁾ = (1,046 0,090 -0,048) ^Т.Это значит: х₁=1,046; х₂=0,090; х₃=-0,046.

Контрольные вопросы и задания для самостоятельной подготовки:

1. Общий вид и свойства системы уравнений.

2. Матричная форма системы уравнений.

3. Методы решения систем линейных уравнений. Метод обратной матрицы.

4. Методы решения систем линейных уравнений. Метод Крамера.

5. Методы решения систем линейных уравнений. Метод Гаусса.

6. Вычисление обратной матрицы методом Гаусса.

7. Системы однородных линейных уравнений, их решение.

8. Фундаментальная система решений.

9. Решить систему линейных уравнений методом Крамера: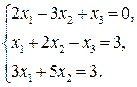

10. Методом Гаусса решить систему: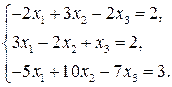

11. Решить систему линейных уравнений методом Крамера: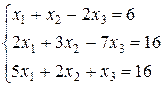

12. Решить систему линейных уравнений методом Гаусса: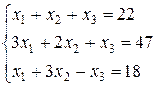

13. Решить систему линейных уравнений методом Крамера: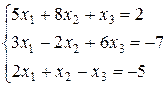

14. Решить систему линейных уравнений методом Гаусса: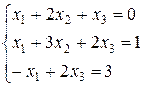

15. Решить систему линейных уравнений методом Крамера: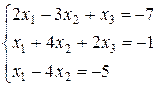

16. Решить систему линейных уравнений методом Гаусса: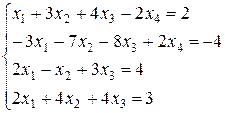

17. Решить систему линейных уравнений методом Крамера: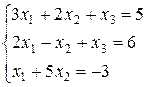

18. Решить систему линейных уравнений методом Гаусса: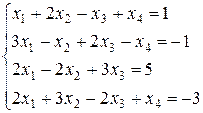

Дата добавления: 2014-10-23