Уравнения линий и поверхностей

Тема 4. Элементы аналитической геометрии на прямой, плоскости и в трехмерном пространстве.

В данной теме рассматривается: уравнение линии на плоскости; уравнение прямой; условие параллельности и перпендикулярности прямых; расстояние от точки до прямой; окружность и эллипс; гипербола и парабола; понятие об уравнении плоскости и прямой в пространстве.

Определение. Множество (совокупность, семейство) точек плоскости с введенной системой декартовых координат, координаты каждой из которых удовлетворяют уравнению F(x,y)=0, называют линия на плоскости, а само уравнение – уравнением этой линии.

Даже в случае отсутствия фактической линии в аналитической геометрии уравнение принято называть уравнением линии. Например, уравнение х2+у2+9=0 только внешне похоже на уравнение окружности, а фактически таковой не представляет. И тогда его называют уравнением мнимой окружности.

Следуя определению, можно рассматривать два типа задач:

1-й тип – дано уравнение и требуется изобразить линию;

2-й тип – дано описание линии и требуется по этому описанию составить(вывести, получить) уравнение линии.

Первый тип частично решен еще в школьном курсе и частично будет решаться в разделах 3 и 4. Второй тип решается всегда по одной и той же схеме:

1-й шаг – берем произвольную точку М(х;у) и предполагаем, что она принадлежит искомой линии;

2-й шаг – математическими средствами связываем координаты точки М и характеристики линии из ее описания и получаем уравнение линии.

В некоторых случаях вместо указанных двух этапов используют готовые шаблоны уравнений. Делают это если такие шаблоны есть в наличии (см. 6.2,6.4).

Пример 6.1. Составить уравнение линии, каждая точка которой равноудалена от концов отрезка АВ, где А(-1;0), В(3;0).

Решение. Из геометрии известно, что искомая линия – серединный перпендикуляр. Получим его уравнение. Возьмем М(х;у). Пусть М принадлежит искомой линии. Тогда справедливо равенство АМ=ВМ. Фактически мы уже записали уравнение линии. Остается его преобразовать к виду F(x,y)=0. Известно, что АМ=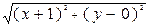. Аналогично ВМ=. Получаем =. Полученное гораздо ближе к требуемому. Остаетс преобразовать его и получить окончательно х=1.

Определение. Множество точек пространства с введенной системой координат, координаты каждой из которых удовлетворяют уравнению F(x,y,z)=0, называют поверхностью. А уравнение – уравнением поверхности в пространстве.

Для этого определения справедливы те же задачи, что и выше как и схема их решений.

Определение. Систему 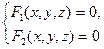принято называть уравнениями линии в пространстве.

Как видим, для линии следует говорить ‘уравнения линии’.

Определение. Алгебраическими линиями(поверхностями) называют линии (в пространстве или на плоскости), уравнения которых представлены полиномами от переменных.

Определение. Порядок линии (поверхности) – это суммарная наивысшая степень переменных в каждом слагаемом полинома.

Дата добавления: 2014-10-23