Тема 1. Основные понятия комбинаторики

Элементы математической статистики.

Основные понятия и термины: комбинаторика, элементы комбинаторики, перестановка, факториал, сочетания, размещения

Краткое изложение теоретических вопросов:

Комбинато́рика — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей, и имеет широкий спектр применения в различных областях знаний (например в генетике, информатике, статистической физике).

Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

Перестановкой из n элементов (например чисел 1,2,…,n) называется всякий упорядоченный набор из этих элементов.

Число всех перестановок порядка n равно факториалу: P_n=n!

Факториа́л числа n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел от 1 до n включительно.

По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.

1! = 1,

2! = 2•1 = 2,

3! = 3 •2 •1 = 6,

4! = 4 •3 •2 •1 = 24,

Задача. Сколькими способами можно выложить в ряд красный, черный, синий и зеленый шарики?

Решение:

На первое место можно положить любой из четырех шариков, на второе – любой из трех оставшихся, на третье – любой из двух оставшихся, а на четвертое – последний оставшийся шарик. Итак, ответ: 4 • 3 • 2 • 1 = 4!.

Задача. На танцплощадке собрались 7 юношей и 7 девушек. Сколькими способами они могут разбиться на пары для участия в очередном танце?

Ответ: 7!

Правило умножения заключается в том, что для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.

Задача. Сколько четных двузначных чисел можно составить из цифр 0, 2, 3, 6, 7, 9?

Решение. Перечислим все возможные варианты:

20 22 26

30 32 36

60 62 66

70 72 76

90 92 96

Используя правило умножения, получаем: 5х3=15

Сочетаниями из n элементов по k называются соединения, которые можно образовать из n элементов, собирая в каждое соединение k элементов; при этом соединения отличаются друг от друга только самими элементами (различие порядка их расположения во внимание не принимается).

Например, из 3 элементов (a,b,c) по 2 можно образовать следующие сочетания: ab, ac, bc.

Число сочетаний из n элементов по k обозначают C_n^k. Оно равно

Задача. Сколько экзаменационных комиссий, состоящих из 3 членов, можно образовать из 10 преподавателей?

Решение: По формуле находим:

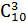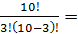=120 комиссий

Ответ: 120 комиссий.

Размещением называется расположение “предметов” на некоторых “местах” при условии, что каждое место занято в точности одним предметом и все предметы различны.

В отличие от сочетаний размещения учитывают порядок следования предметов. Так, например, наборы < 2,1,3 > и < 3,2,1 > являются различными, хотя состоят из одних и тех же элементов {1,2,3} (то есть, совпадают как сочетания).

Термин “Размещение” употребил впервые Якоб Бернулли в книге “Искусство предположений”.

Задача. В группе обучается 24 студента. Сколькими способами можно составить график дежурства по техникуму, если группа дежурных состоит из трех студентов?

Решение: число способов равно числу размещений из 24 элементов по 3, т.е. равно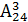. По формуле находим

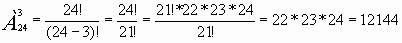
Ответ: 12144 способа

Задачи на подсчет числа размещений, перестановок, сочетаний.

	Сколько различных слов можно составить из слова «ВЕКТОР»;
	В соревнованиях по фигурному катанию принимали участие россияне, итальянцы, украинцы, немцы, китайцы и французы. Сколькими способами могут распределиться места по окончании соревнований?
	Сколько флагов можно составить из трех цветных полосок?
	Саша, Петя, Денис, Оля, Настя часто ходят в кафе. Каждый раз, обедая там, они рассаживаются по-разному. Сколько дней друзья смогут это сделать без повторения?
	Для участия в первенстве университета по легкой атлетике необходимо составить команду из 5 человек. Сколькими способами это можно сделать, если имеется 7 бегунов?
	Для освещения событий в одной из стран ближнего зарубежья решено отправить трех корреспондентов газеты. Сколькими способами это можно сделать, если в штате 32 сотрудника?
	В финале конкурса <Студент года> принимают участие 6 человек. Сколькими способами могут распределиться три призовых места?

Дата добавления: 2014-10-23