Уравнение Навье-Стокса для вязкой жидкости

Рассмотрим изотермическое движение вязкой несжимаемой жидкости. В этом случае плотность и вязкость будут величинами постоянными.

Подставим выражения компонент напряжений 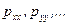в соответствии с формулами (5.20) - (5.22) и (5.29) в уравнения в напряжениях (4.31) и, учитывая, что для несжимаемой жидкости

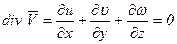, (5.30)

получим уравнение движения вязкой несжимаемой жидкости. Так, для проекции на ось х найдем

(5.31)

Проделав аналогичные преобразования с двумя другими уравнениями (4.31), будем иметь систему уравнений

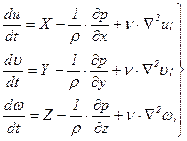(5.32)

где 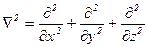- оператор Лапласа.

Уравнения (5.32) представляют собой замкнутую систему с четырьмя неизвестными 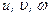и р. Величины и 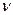, а также проекции массовых сил X, У и Z должны быть заданы.

Вспоминая выражение для ускорения (3.10), видим, что уравнения (5.32) представляют собой нелинейные дифференциальные уравнения в частных производных второго порядка. В векторной форме они имеют вид

, (5.33)

где 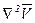- вектор с проекциям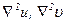и и .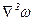

Уравнения (5.32) впервые были получены в 1845 г. Стоксом и поэтому часто называются уравнениями Стокса.

Для решения системы (5.32) следует задать граничные условия. При наличии же локальных составляющих ускорения, т.е. в нестационарном потоке, необходимы и начальные условия.

Начальные условия ставятся так же, как и для идеальной жидкости, в виде распределения скоростей во всей рассматриваемой области в момент времени , т.е. задается вид функций

.

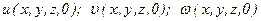Граничные условия задаются на поверхности обтекаемого тела и на бесконечности, в невозмущенной жидкости. На бесконечности, как правило, считают известными величины скорости и давления, а для внутренней задачи - расход жидкости.

Тип граничных условий для любого уравнения в частных производных, называют именами известных ученых: Дирихле, Неймана или Робина.

Условие Дирихле соответствует случаю, когда на границе замкнутой области задано значение искомой функции, т.е. и = f. Если на границе замкнутой области задано значение не самой искомой функции, а лишь ее производной по нормали, т.е. ди/дп= f, то такое граничное условие называют условием Неймана. Смешанные граничные условия Дирихле и Неймана в виде ди / дп + ku = f, где k > 0, носят название граничного условия Робина.

Дата добавления: 2014-10-31