Уравнения движения в напряжениях

Это уравнение можно получить путем применения теоремы об изменении количеств движения к некоторому элементарному объему 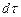сплошной среды. В соответствии с ранее сказанным все внешние силы складываются из массовых и поверхностных. Следовательно, главный вектор внешних сил можно представить как сумму двух указанных главных векторов сил: объемных 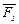и поверхностных 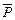. Тогда в соответствии с теоремой об изменении количеств движения получим

. (4.15)

Но 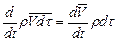, (4.16)

так как есть масса жидкости в объеме 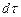, которая остается постоянной во все время движения.

Используя последнее соотношение, получим выражение известного в механике принципа Даламбера

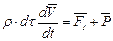, (4.17)

согласно которому уравнение динамики можно свести к уравнению статики, если к внешним силам присоединить силы инерции.

Применим теорему об изменении количеств движения к массе, заключенной в объеме элементарного параллелепипеда со сторонами dx, dy и dz. Тогда вектор массовых сил можно представить в виде

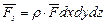, (4.18)

где 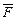- вектор массовых сил, отнесенный к единице массы.

Найдем теперь главный вектор поверхностных сил. На рис. 4.3 показаны напряжения поверхностных сил, приложенных к граням, нормальным к оси х. Легко показать аналогичную схему напряжений, приложенных к граням, нормальным к осям у и z.

Рис. 4.3. Схема напряжений поверхностных сил

Спроектируем составляющие поверхностных сил на ось х. Рассмотрение сил, приложенных к граням, нормальным к оси х приводит к выражению

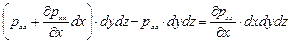, (4.19)

к граням, нормальным к оси у, -

, (4.20)

к граням, нормальным к оси z -

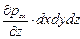. (4.21)

Таким образом, проекция главного вектора поверхностных сил на ось х будет

. (4.22)

Соответственно проектирование на оси у и z дает

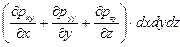; (4.23)

. (4.24)

Тогда в соответствии с формулой получим уравнения, отнесенные к единице объема, в проекциях на прямоугольную систему координат

; (4.25)

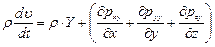; (4.26)

. (4.27)

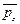Так как вектора напряжений поверхностных сил и , приложенных к площадкам, нормальным осям х, у и z, равны

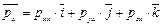; (4.28)

; (4.29)

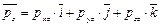, (4.30)

то уравнение в векторном виде будет

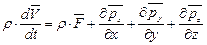. (4.31)

Эти уравнения являются уравнениями движения сплошных сред в напряжениях; в дальнейшем их будем называть уравнениями в напряжениях.

Дата добавления: 2014-10-31