Напряжения поверхностных сил

Поверхностные силы, действующие в движущихся сплошных средах, существенно отличаются от поверхностных сил, действующих в покоящейся среде. Это отличие заключается не только в появлении касательных составляющих, которые в покоящейся жидкости отсутствуют, а также и в том, что нормальные составляющие сил изменяют свою величину. Найдем величины, определяющие поверхностные напряжения в некоторой точке сплошной среды. Для этого рассмотрим в движущейся жидкости элементарный тетраэдр с вершиной в точке О (рис. 4.2).

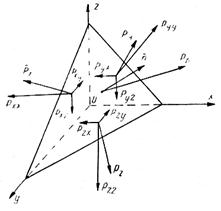
Рис. 4.2. Расчетная схема элементарного тетраэдра

Площади боковых граней тетраэдра равны 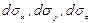, причем индексы означают ось, перпендикулярно которой расположена грань. Наклонная грань имеет площадь, равную 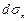; n - нормаль к этой грани. К каждой из рассматриваемых граней будут приложены поверхностные силы, в общем случае направленные под некоторым углом к грани. Обозначим вектор напряжения поверхностных сил, приложенных к грани, перпендикулярной оси х, через 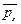соответственно к граням, нормальным к осям у и z, через 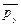и 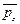. К наклонной грани приложено напряжение 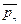. Как видно из рис. 4.2

;

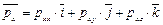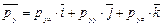; (4.7)

.

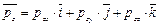Второй индекс у проекций напряжений означает ось, на которую проектируются векторы напряжени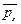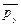й , и .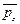

Зная 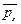, 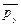и 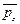, можно определить вектор поверхностных сил 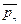, приложенный к площадке с любым заданным направлением орта нормали n.

Действительно, написав уравнение движения центра инерции тетраэдра с массой dm, получим

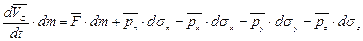, (4.8)

где 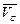- скорость центра инерции тетраэдра;

F - плотность массовых сил.

Члены в уравнении, содержащие элементарную массу, являются величинами третьего порядка малости, в то время как остальные - второго порядка малости. Поэтому величинами, содержащими dm, пренебрегаем. Получим

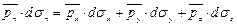. (4.9)

Из рис. 4.2 видно, что

;

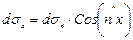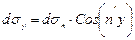; (4.10)

,

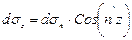поэтому

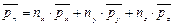, (4.11)

где ;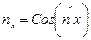

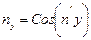; (4.12)

.

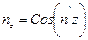Можно получить проекции вектора напряжений поверхностных сил, приложенных к площадке с любым заданным направлением n, на координатные оси х, у и z:

;

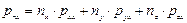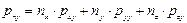; (4.13)

;

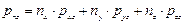Напряжение в точке определяется совокупностью величин

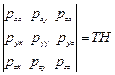. (4.14)

Таблица величин, определяющих напряженное состояние в точке, называется тензором напряжений. Составляющие 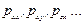будем называть компонентами тензора напряжений или просто компонентами напряжений.

Дата добавления: 2014-10-31