Через поверхность

Расход элементарной струйки и расход

Расходом называется количество жидкости, протекающее через живое сечение потока (струйки) в единицу времени. Под живым сечением, или просто сечением потока, понимают в общем случае поверхность в пределах потока, проведенную нормально к линиям тока.

Это количество можно измерить в единицах объема, в весовых единицах или в единицах массы, в связи с чем различают объемный Q, весовой 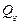и массовый 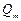расходы. Для элементарной струйки, имеющей бесконечно малые площади сечений, можно считать истинную скорость V одинаковой во всех точках каждого сечения. Следовательно, для этой струйки объемный (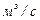), весовой (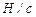) и массовый (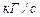) расходы будут равны

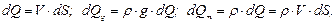(3.14)

где dS - площадь сечения струйки.

Основываясь на законе сохранения вещества, на предположении о сплошности (неразрывности) течения и на указанном выше свойстве трубки тока, заключающемся в ее «непроницаемости», для установившегося течения несжимаемой жидкости можно утверждать, что объемный расход во всех сечениях элементарной струйки один и тот же

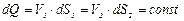(вдоль струйки). (3.15)

Это уравнение называется уравнением объемного расхода для элементарной струйки.

В векторном анализе потоком любого вектора а называется интеграл по некоторой поверхности 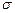от проекции вектора а на нормаль n в каждой точке поверхности, т.е.

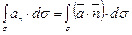. (3.16)

Соответственно с этим поток вектора скорости 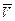определяется величиной, равной

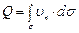. (3.17)

Поток вектора скорости физически представляет собой объемный расход некоторой жидкости (среды) через поверхность .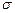

Если поверхность 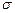замкнутая, то при отсутствии внутри поверхности источников и стоков поток вектора скорости через замкнутую поверхность будет равен нулю

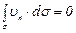. (3.18)

Для потока конечных размеров скорость имеет различное значение в разных точках сечения, поэтому расход надо определять как сумму элементарных расходов струек, т.е.

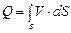. (3.19)

Обычно в рассмотрение вводят среднюю по сечению скорость , откуда получаем

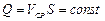(вдоль потока). (3.20)

Для потока конечных размеров, ограниченного непроницаемыми стенками, будем иметь

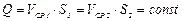(вдоль потока). (3.21)

Уравнение расхода является следствием общего закона сохранения вещества для частных условий, в частности для условий сплошности (неразрывности) течения.

При наличии источника поток вектора скорости 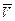будет составлять

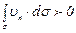, (3.22)

а при наличии стока

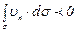. (3.23)

Дата добавления: 2014-10-31