Уравнение неразрывности (сплошности)

В механике обычно рассматриваются законы сохранения четырех величин: массы, количества движения, момента количества движения и энергии. Все законы сохранения относятся к так называемым изолированным системам. Будем в дальнейшем называть систему изолированной или замкнутой в том случае, если через контрольную поверхность - окружающую систему - нет переноса массы, количества движения и энергии. На изолированную систему не действуют внешние силы.

Закон сохранения массы для изолированной системы выражается в том, что масса m такой системы остается постоянной во все время движения, т.е. количество вещества остается постоянным или

. (3.24)

Общий закон сохранения массы применительно к сплошным средам получает свое выражение в уравнении неразрывности или сплошности движения. Для получения этого уравнения при отсутствии источников или стоков массы применим закон сохранения массы к некоторому элементарному объему 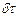, движущемуся вместе со средой, имеющей плотность 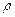. Так как

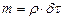(3.25)

то 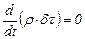, (3.26)

или 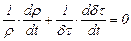. (3.27)

Относительное изменение объема 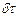в данной точке за единицу времени равно дивергенции вектора скорости в данной точке, т.е.

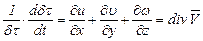. (3.28)

Тогда уравнение неразрывности движения примет вид

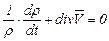. (3.29)

Если плотность зависит и от времени и от координат, т.е. 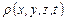, то

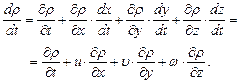(3.30)

Подставив это выражение в (3.29), получим другой вид уравнения неразрывности (в проекциях на прямоугольные оси)

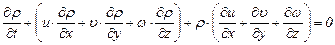(3.31)

или

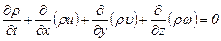. (3.32)

Последние слагаемые составляют дивергенцию 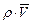, поэтому уравнение (3.32) в дифференциальной форме имеет вид

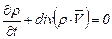. (3.33)

Для стационарного движения, при котором 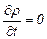, уравнение неразрывности примет вид

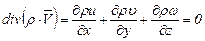. (3.34)

При наиболее простом случае движения, когда плотность жидкости постоянна и не зависит от координат и времени, т.е. 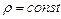, уравнение неразрывности будет иметь вид

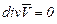. (3.35)

Уравнение неразрывности (сплошности) также может быть представлено в интегральной форме в виде

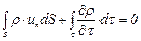, (3.36)

где S - поверхность, ограничивающая объем .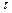

Дата добавления: 2014-10-31