Шаг 0 расчетов по алгоритму Флойда

Построение матрицы путей и матрицы переходов графа G

Тема: «Поиск кратчайших путей на неориентированном графе по алгоритму Флойда».

Расчетно-графическая работа №8

1 Теоретическая часть

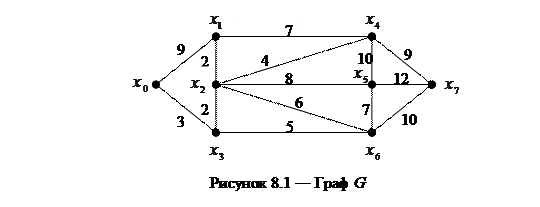
Пусть задан граф G (рисунок 8.1).

Алгоритма Флойда использует две матрицы размера 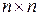, где 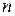-число вершин графа: 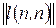- матрицу кратчайших путей и 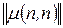- матрицу кратчайших переходов. На рисунке 8.2изображены обе эти матрицы для графа G (рисунок 8.1).

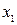
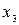
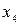
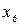
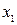
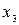
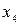
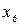
а) б)

Рисунок 8.2 ― Матрицы кратчайших путей а) и кратчайших переходов б) графа G

Матрица переходов производна относительно матрицы путей. Для p=0 (т.е. нулевого шага работы алгоритма) элементы матрицы есть концевые вершины из перехода из в 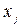. Поэтому в каждом столбце 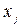матрицы указана вершина .

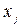Принимаем p=0. Принимаем в матрице вершину за базовую и выделяем (штриховкой) базовую строку и базовый столбец (рис. 8.3).

Рисунок 8.3 ―Матрица путей на нулевом шаге расчетов

Вычеркиваем в матрице строки столбцы, базовые элементы которыхимеют значения (они на рис. 8.3 показаны более темной штриховкой), так как и 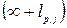всегда больше конечного значения . В итоге получаем матрицу 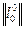, изображенную на рисунке 8.4.

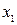
Рисунок 8.4 - Матрица 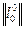после вычеркивания строк и столбцов, базовые элементы которых имеют значение

Изобразим на рисунке 8.5 граф 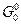по матрице .

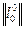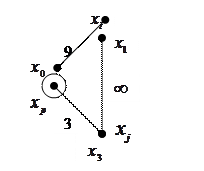
Обозначения: в окружность заключена базовая вершина ; каждая вершина идентифицирована дважды: переменной 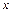с индексом- цифрой и переменной 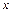с индексом-буквой

Рисунок 8.5 ― Граф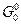

Выполним расчеты, для чего будем проверять справедливость соотношения:

Для графа 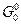на рисунке 8.5 это означает, что проверяется справедливость соотношения:

или иными словами: сравнивается суммарная длина пути из первой вершины 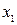до базовой , т.е. 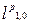и из нулевой вершины до вершины 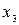, т.е. с длиной пути из первой вершины в третью «напрямую», т.е. (см. рис. 8.5).

Итак, проверяем справедливость соотношения:

?

Ответ - Да.

Тогда:

1) ,

;

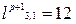2) ,

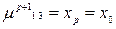Вносим изменения в матрицу и (рис. 8.6): изменяем элемент , на 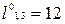; , . Изменения выделены на рис. 8.6 красным квадратом.

								Базовая строка

	Базовый столбец

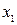
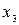
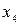
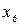
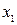
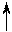
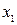
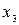
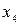
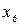
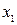
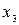
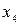
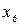
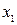
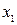
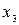
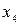
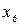
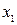
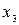
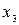
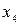
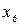
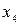
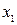
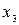
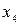
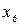
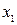
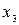
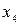
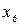
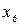
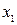
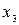
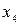
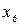
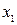
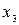
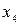
Рисунок 8.6 ― Матрицы путей и переходов графа G перед началом шага p=1

Дата добавления: 2014-10-31