Использование результатов расчетов по алгоритму Флойда

Проверка результатов расчетов по алгоритму Флойда

С целью проверки полученных результатов выберите три варианта начальных и конечных вершин Вашего пути по графу G. Определите по графу G методом визуального анализа кратчайший путь для каждого из трех вариантов. Для каждого варианта запомните вершины, через которые проходит кратчайший путь. Повторите расчеты, но с использованием матриц кратчайших путей и кратчайших переходов. Сравните результаты. Если они совпадают, то будем считать, что расчеты матриц по алгоритму Флойда выполнены с определенной степенью достоверности правильно. Отразите результаты проверки в отчете о выполнении расчетно-графической работы. Если результаты визуального анализа графа и анализа матриц не совпадают, необходимо проверить расчеты.

Таким образом, в результате расчетов получены матрицы кратчайших путей и кратчайших переходов графа G.

По матрицам 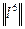и можно найти длину кратчайшего пути и соответствующий этому пути переход.

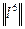Пусть нас интересует длина кратчайшего пути между вершинами и . Обратимся к матрице (рисунок 8.16). На пересечении строки и столбца находим, что длина кратчайшего пути равна 18-ти единицам.

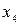Для поиска соответствующего перехода будем сочетать анализ матрицы с визуальным анализом графа (рис. 8.1). По матрице определяем, что кратчайший путь из в лежит через вершину (пересечение строки и столбца ). Из вершины 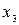в вершину 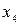через вершину (пересечение строки 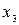и столбца ).

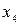Таким образом, кратчайший переход между вершинами и опирается на вершины .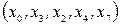

2 Задание

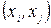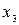Задание на РГР формулируется следующим образом: «Найти кратчайшие пути на неориентированном графе G (рисунок 8.17) по алгоритму Флойда. Протяженность (вес) ребра приведены в таблице 8.1, где - означает отсутствие ребра , а «1» - его наличие, которое необходимо умножить на вес ребра. 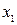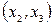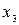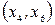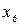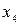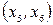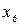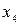Для вариантов 1-10 ребро является дугой с направлением от вершины к , для вариантов 11-20 ребро - дугой с направлением от вершины к , для вариантов 21-30 ребро - дугой с направлением от вершины к , для вариантов 31-40 ребро - дугой с направлением от вершины к , для вариантов 41-50 ребро - дугой с направлением от вершины к ».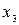

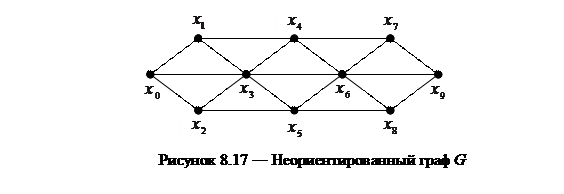
Таблица 8.1 ― Данные для формирования графа G по вариантам

Старший разряд номера варианта	Индексы вершин, инцидентных ребру
0,1	0,2	0,3	1,3	1,4	2,3	2,5	3,4	3,5	3,6
Вес ребра (условных единиц)

Таблица 8.1 ― Продолжение

Младший разряд номера варианта	Индексы вершин, инцидентных ребру
4,6	4,7	5,6	5,8	6,7	6,8	6,9	7,9	8,9
Вес ребра (условных единиц)

3 Содержание отчета

1) Условие задачи в соответствии с вариантом.

2) Пошаговый подробный поиск кратчайших путей на неориентированном графе по алгоритму Флойда.

3) Проверка результатов расчетов по алгоритму Флойда.

4) Выводы.

4 Список литературы

1. Пономарев В.Ф. Дискретная математика для инженеров.- Калининград: ФГОУ ВПО КГТУ, 2010.- 351 с.

Дата добавления: 2014-10-31