
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Шаги «2 – 6» расчетов
|
|
|
|
Шаг «1» расчетов
Зададим в правой части таблицы 7.2 множество ребер инцидентных вершинам подграфа № 1 графа G на рисунке 7.2. Таковых будет семь. Выберем из них ребра с минимальными значениями весов. Таковых два: 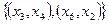 . Остановим выбор на ребре
. Остановим выбор на ребре 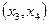 , что покажем, заключив его в прямоугольник в таблице 7.2. Тогда ребро
, что покажем, заключив его в прямоугольник в таблице 7.2. Тогда ребро  вычеркнем из данной строки таблица 3. Это ребро используется в дальнейших расчетах.
вычеркнем из данной строки таблица 3. Это ребро используется в дальнейших расчетах.
Таблица 7.3- Размер кратчайшего остова графа G
| Шаг p | 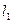
| 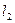
| 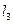
| 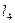
| 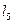
| 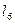
| 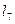
| 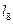
| 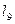
| 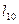
| 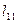
| 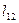
| 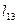
| 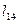
| 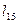
| 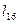
| 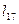
| 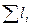
|
| Суммарная длина ребер минимального остова графа G: |
Таблица 7.2 ― Результаты выбора подграфов графа G
| Шаг p | Вершины графа G | Множество ребер графа G, смежных с вычисленным подграфом минимального остова графа G | |||||||
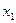
| 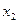
| 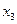
| 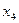
| 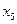
| 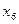
| 
| 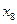
| ||
  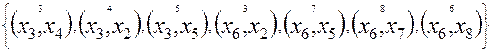
| |||||||||
 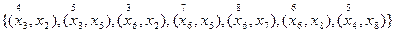
| |||||||||
 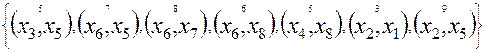
| |||||||||
  
| |||||||||
  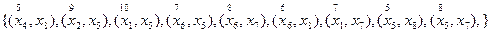
| |||||||||
   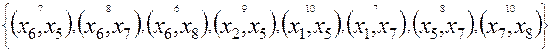
| |||||||||
Выполняются аналогично расчетам на шаге 1. Особенностью расчетов во время выполнения шагов 2 – 6 оказалось, что на шаге 5 в таблице 7.2 получено множество из восьми ребер. Поскольку присоединение дуг 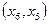 или
или 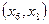 формировало бы на подграфе кратчайшего остова цикл их необходимо отбросить и остановить выбор на дуге
формировало бы на подграфе кратчайшего остова цикл их необходимо отбросить и остановить выбор на дуге 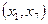 .
.
Результаты расчетов на шагах 2 – 6 сведены в таблицы 7.2, 7.3. На рисунке 7.4 показано изменение по шагам подграфов минимального остова графа G.
Выводы
Таким образом, в результате расчетов по алгоритму Дейкстра сформирован минимальный остов графа G (см. результаты на шаге 6, рисунок 7.4) с суммарной длиной дуг – 30.
 Добавим к подграфу на рисунке 7.2 ребро
Добавим к подграфу на рисунке 7.2 ребро 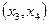 и получим подграф № 2 на рисунке 7.3.
и получим подграф № 2 на рисунке 7.3.
Обведем пунктиром подграф № 2 графа G на рисунке 7.1. Заполним первые строки матрицы 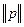 в таблице 7.3.
в таблице 7.3.
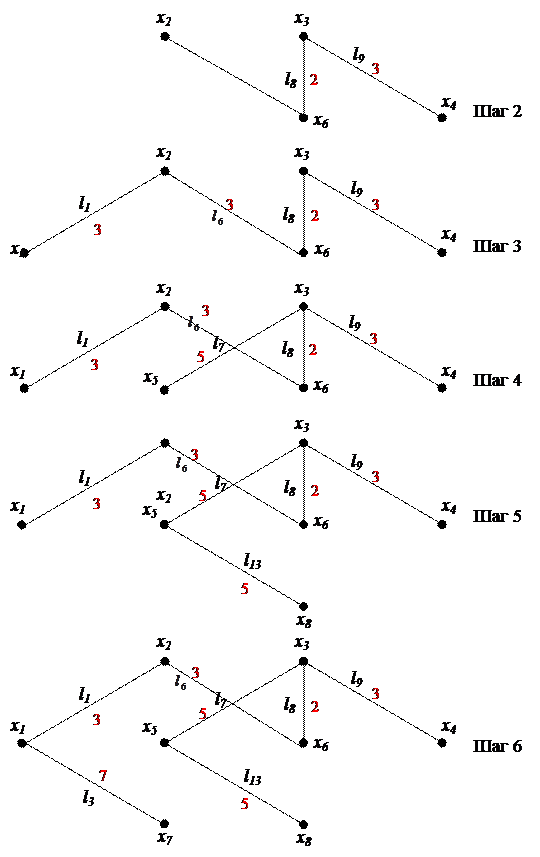
Рисунок 7.4 ― Изменение по шагам подграфов минимального остова
графа G
2 Примеры решения задач
Упражнение 1
Тема: «Графы. Основные понятия. Графы и отношения. Маршруты, пути, цепи, циклы»
Задачи для решения в аудитории
1. Задать матрицами инцидентности и смежности граф, изображенный на рис.
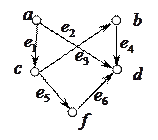
2. Пусть ориентированный граф G на рисунке ниже задает отношение R. Каковы свойства отношения?

3. Изобразить графы, соответствующие отношениям, представленным следующими матрицами:
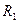
| a | b | c | d |
| a | ||||
| b | ||||
| c | ||||
| d |
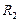
| a | b | c | d |
| a | ||||
| b | ||||
| c | ||||
| d |
4. Для вершин 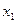 и
и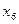 графа
графа 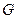 на рисунке ниже привести примеры маршрута, простого маршрута. Определить цикл, приняв вершину
на рисунке ниже привести примеры маршрута, простого маршрута. Определить цикл, приняв вершину 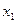 на начало и конец цикла. Есть ли на этом графе эйлеров маршрут и (или) гамильтонов маршрут?
на начало и конец цикла. Есть ли на этом графе эйлеров маршрут и (или) гамильтонов маршрут?

5. Для четырех графов на рисунке ниже определить расстояния между вершинами.


6. Какими свойствами обладает отношение связанности вершин графа, изображенного на рисунке ниже.

Домашнее задание
1. Построить матрицы смежности и инцидентности графов, изображенных на рисунках ниже. Нумерацию вершин и ребер (дуг) задайте самостоятельно.
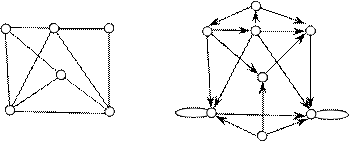
2. Имеют ли графы эйлеров цикл (цепь)? Запишите цикл.

3. Имеют ли пятигранник-призма и пятиугольник с петлями в некоторых вершинах гамильтонов цикл (цепь)?
4. Каковы расстояния между вершинами в графе на рисунке ниже.

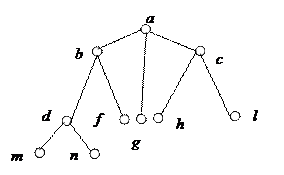
5. На рисунке ниже. Показан граф-дерево. Сколько листьев на графе? Определите множество листьев. Сколько ветвей для вершины d на графе. Какая вершина является корнем? Можно ли принять любую вершину графа-дерева за корень? Перерисуйте граф-дерево с другим корнем.
6. Изобразите граф-лес.
7. Достижима ли:
1) вершина h из вершины a;
2) вершина a из вершины m
для графа, изображенного на рисунке ниже. Если – да, то задайте множество путей.
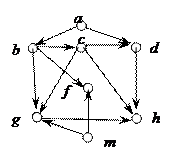
8. Какие вершины являются центрами четырех графов на рисунке? Чему равны радиусы графов?

9. Задайте множество маршрутов графа-дерева в задаче 5.
10. Постройте граф с гамильтоновым циклом.
Упражнение 2
Тема: «Бинарные операции над графами. Изоморфизм графов»
Задачи для решения в аудитории
1.  Найти объединение графов
Найти объединение графов 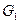 и
и  , представленных на рис.
, представленных на рис.
1)
2)
3)
4)
5)
2. Найти пересечение графов, представленных на рисунке в задаче 1.
3. Найти объединение и пересечение графов  и
и 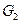 ,
,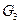 и
и 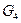 изображенных на рисунках ниже.
изображенных на рисунках ниже.
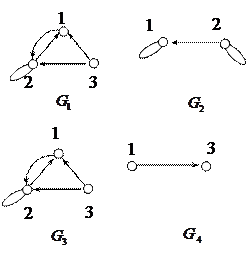
4. Найти разность графов, изображенных на рисунке ниже.
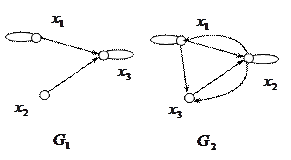
5. Найти композицию графов, изображенных на рисунке ниже.

6. Изоморфны ли графы, изображенные на рисунке ниже.

7. Изоморфны ли графы, изображенные на рис.
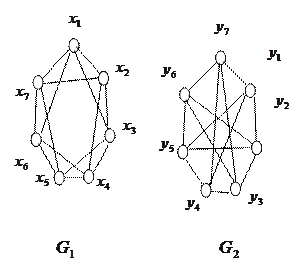
Домашнеезадание
1. Найти объединение графов:
 |
1)
2)
2. Найти попарно пересечение графов для варианта 1 и 2:
 |
1)
2)
3. Найти разность двух подграфов полного графа:

4. Найти модульное произведение двух графов:

5. Найти декартову сумму графов  и
и 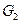
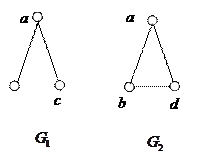
6. Удалите вершины 1,2, 8, 9 графа на рисунке ниже. Удаление выполнить с помощью матрицы инциденций и графически.

7. Постройте композицию двух графов:

8. Постройте композицию двух графов:

9. Постройте два изоморфных подграфа полного графа с четырьмя вершинами. Покажите их изоморфность алгоритмическим путем.
10. Определить, изоморфны ли графы.

3 Задание
Задание на РГР формулируется следующим образом: «Найти кратчайший остов неориентированного графа G (рисунок 7.5) по алгоритму Дейкстра. Протяженность (вес) ребер приведены в таблице 7.4, где  - означает отсутствие ребра (
- означает отсутствие ребра (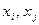 ), а «1» - его наличие, которое необходимо умножить на вес ребра. Для вариантов 1 –10 начальной вершиной является
), а «1» - его наличие, которое необходимо умножить на вес ребра. Для вариантов 1 –10 начальной вершиной является 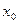 , для вариантов 11 – 20 – вершина
, для вариантов 11 – 20 – вершина 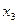 , для вариантов 21 – 30 – вершина
, для вариантов 21 – 30 – вершина 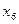 , для вариантов 31 – 40 – вершина
, для вариантов 31 – 40 – вершина 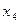 , для вариантов 41 – 50 – вершина
, для вариантов 41 – 50 – вершина 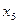 ».
».
 |
Рисунок 7.1 ― Неориентированный граф G
Таблица 7.4 ― Данные для формирования графа G по вариантам
| Старший разряд номера варианта | Индексы вершин, инцидентных ребру | |||||||||
| 0,1 | 0,2 | 0,3 | 1,3 | 1,4 | 2,3 | 2,5 | 3,4 | 3,5 | 3,6 | |
| Вес ребра (условных единиц) | ||||||||||

| ||||||||||

| ||||||||||

| ||||||||||

| ||||||||||

| ||||||||||

| ||||||||||

| 
| |||||||||

| ||||||||||

| ||||||||||

|
Таблица 7.4 ― Продолжение
| Младший разряд номера варианта | Индексы вершин, инцидентных ребру | |||||||||
| 4,6 | 4,7 | 5,6 | 5,8 | 6,7 | 6,8 | 6,9 | 7,9 | 8,9 | ||
| Вес ребра (условных единиц) | ||||||||||

| ||||||||||

| ||||||||||

| ||||||||||

| ||||||||||

| ||||||||||

| ||||||||||

| ||||||||||

| ||||||||||

|
4 Содержание отчета
1) Условие задачи в соответствии с вариантом.
2) Пошаговый подробный поиск кратчайшего остова неориентированного графа по алгоритму Дейкстра.
3) Выводы.
5 Список литературы
1. Пономарев В.Ф. Дискретная математика для инженеров.- Калининград: ФГОУ ВПО КГТУ, 2010.- 351 с.
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 956; Нарушение авторских прав?; Мы поможем в написании вашей работы!