Расчет количества ребер m(G) графа G

Расчет количества вершин n(G) графа G

Тема: «Расчет числовых характеристик графов».

Расчетно-графическая работа №6

1 Теоретическая часть

Пусть задан граф G (рисунок 6.1).

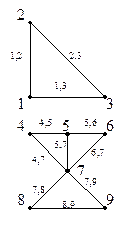Рисунок 6.1 ― Граф G

Расчет выполняется методом визуального анализа графа G. В итоге расчета имеем:

Расчет выполняется методом визуального анализа графа G. В итоге расчета имеем:

Расчет степеней вершин δ_i графа G.

Расчет выполняется методом визуального анализа графа G с целью определения количества ребер (дуг) инцидентных вершине x_i. Результаты расчета сведены в таблицу 6.1.

Таблица 6.1 - Результаты расчета степеней вершин графа G

xi	δi

Расчет числа компонент связности æ(G)

Для расчета числа компонент связности графа G вычисляют матрицу достижимости ||Q^p|| и определяют полные подграфы графа. Для построения матрицы достижимости удобно воспользоваться матрицей смежности графа G:

где ||1|| - единичная матрица (рисунок 6.2),

||H(x_i)|| - матрица смежности графа G,

||H^p(x_i)|| - матрица смежности графа G, возведенная в p -ую степень.

Рисунок 6.2 ― Единичная матрица для графа G

Для возведения в степень матрицы смежности используют правило умножения булевых матриц.

На рисунке 6.3 правило умножения булевых матриц прокомментировано графически.

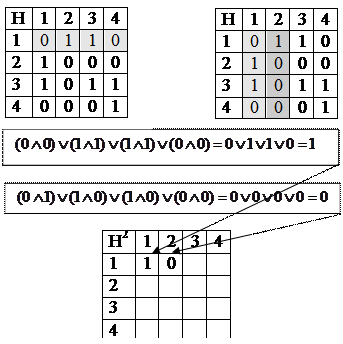Первая строка на второй столбец

Обозначения: - дизъюнкция (см. таблицу истинности в [1]); - конъюнкция (см. таблицу истинности в [1])

Рисунок 6.3 ― Пример умножения булевых матриц 4х4

Построим матрицы смежности графа G (рисунок 6.4).

H

Рисунок 6.4 ― Матрица смежности ||H|| графа G

Возведем матрицу смежности ||H|| в квадрат, т.е. умножим ее саму на себя. Получим ||H²|| (рисунок 6.5).

H^2

Рисунок 6.5 ― Матрица ||H²|| графа G

Возведем матрицу смежности ||H|| в третью степень. Получим ||H³|| (рисунок 6.6).

H^3

Рисунок 6.6 ― Матрица ||H³|| графа G

Анализ матриц ||H²|| и ||H³|| показывает, что никаких изменений в ||H³|| по сравнению ||H²|| нет. Значит процесс вычислений завершен.

Матрица достижимости ||Q³|| (рисунок 6.7) рассчитывается следующим образом:

Q^2

Рисунок 6.7 ― Матрица ||Q²|| графа G

Поскольку матрица ||Q²|| содержит два блока: один – 3х3 элемента, другой – 6х6 элементов, то граф G содержит два связных подграфа:

	G1=<X1, H1>, G2=<X2, H2>,

где X₁={x₁,x₂,x₃}, X₂={x₄,x₅,x₆,x₇,x₈,x₉}.

Таким образом, для исходного графа G=<X,H> число компонент связности равно æ(G)=2.

Расчет цикломатического числа λ(G) графа G

Рассчитаем цикломатическое число графа G, т.е. наименьшее число ребер, удаление которых приведет к графу без циклов и петель.

Расчет выполним по формуле:

	.

В качестве примера удалим на графе G четыре ребра (1,3), (4,5), (5,6), (8,9). Получим граф на рисунке 6.8.

Рисунок 6.8 ― Граф без циклов и петель

Расчет хроматического числа γ(G) графа G

Рассчитаем хроматическое число графа G, т.е. наименьшее число красок при применении которых для раскраски вершин графа две любые смежные вершины графа G, не будут окрашены в один цвет.

Для выполнения расчета воспользуемся двумя оценочными соотношениями. Одно из них задает левую границу для γ(G), min возможное значение γ(G), т.е. γ_min(G):

1) полный n -вершинный граф имеет γ_min(G)=n;

2) пустой граф имеет γ_min(G)=1;

3) граф с циклом (т.е. хотя бы одним) четной длины имеет γ_min(G)=2;

4) граф с циклом нечетной длины имеет γ_min(G)=3;

5) граф-дерево имеет γ_min(G)=2.

Другое оценочное соотношение задает правую границу для γ(G), max необходимое значение γ(G), т.е. γ_max(G):

.

Начинаем проверку с вычисления γ_min(G). Поскольку в графе G есть цикл нечетной длины пробуем раскрасить граф тремя красками (рисунок 6.9).

Рисунок 6.9 ― Раскраска графа G синей, желтой и красной красками

Вывод: трех красок, т.е. γ_min(G) =3 оказалось достаточно:

.

Если бы трех красок оказалось недостаточно, следовало бы γ_min(G) увеличить на единицу и повторить раскраску заново. И так далее, до получения желаемого результата. Однако таких красок не должно быть больше чем γ_max(G).

Дата добавления: 2014-10-31