Графическое представление нормального алгоритма

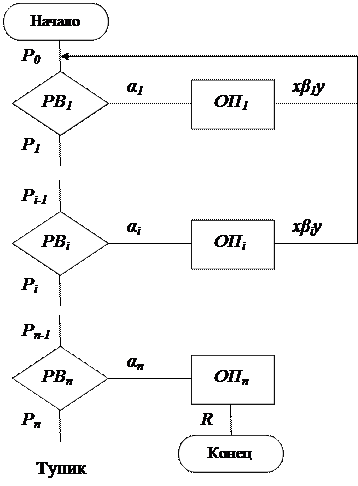где: PB_i ― распознаватель вхождения; ОП_i ― оператор подстановки.

Распознаватели вхождения соединяются последовательно в соответствии с нумерацией правил в схеме.

Пример на составление НАМ (перестановка символов).

Для сокращения формулировки задачи будем использовать следующие соглашения:

– буквой Р будем обозначать входное слово;

– буквой А будем обозначать алфавит входного слова, т.е. набор тех символов, которые и только которые могут входить во входное слово Р (но в процессе выполнения НАМ в обрабатываемых словах могут появляться и другие символы).

Задача: А={a,b}. Преобразовать слово Р так, чтобы в его начале оказались все символы a, а в конце – все символы b.

Например: babba → aabbb

Решение.

Казалось бы, для решения этой задачи нужен сложный НАМ. Однако это не так, задача решается с помощью НАМ, содержащего всего одну формулу:

{ ba → ab

Пока в слове P справа хотя бы от одного символа b есть символ a, эта формула будет переносить a налево от этого b. Формула перестает работать, когда справа от b нет ни одного a, это и означает, что все a оказались слева от b.

Например:

babba → abbba → abbab → ababb → aabbb

Алгоритм остановился на последнем слове, т.к. к нему уже неприменима наша формула.

В НАМ легко реализуются перестановки, вставки и удаления символов. Однако в НАМ возникает другая проблема: как зафиксировать символ (подслово), который должен быть обработан? Рассмотрим эту проблему на следующем примере.

Пример на составление НАМ (использование спецзнака).

Задача: А ={ a,b }. Удалить из непустого слова Р его первый символ. Пустое слово не менять.

Решение.

Ясно, что удалив первый символ слова, надо тут же остановиться. Поэтому, казалось бы, задачу решает следующий НАМ:

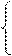
a (1)

b (2)

Однако это неправильный алгоритм, в чём можно убедиться, применив его к слову bbaba:

bb a ba bbba

Как видно, этот НАМ удалил не первый символ слова, а первое вхождение символа a, а это разные вещи. Данный алгоритм будет правильно работать, только если входное слово начинается с символа a. Ясно, что перестановка формул в этом НАМ не поможет, т.к. тогда он будет, напротив, неправильно работать на словах, начинающихся с a.

Что делать? Надо как-то зафиксировать, пометить первый символ слова, например, поставив перед ним какой-либо знак, скажем *, отличный от символов алфавита слова. После этого уже можно с помощью формул вида *ξ заменить этот знак и первый символ ξ слова на пусто и остановиться:

bbaba → * bbaba baba

А как поставить * перед первым символом? Это реализуется формулой →* с пустой левой частью, которая, по определению, приписывает свою правую часть слева к слову.

Итого, получаем следующий НАМ:

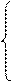→* (1)

*a (2)

*b (3)

Проверим его на том же входном слове:

bbaba → * bbaba → ** bbaba → *** bbaba → …

Как видно, этот алгоритм постоянно приписывает слева звёздочки. Почему?

Напомним, что формула постановки с пустой левой частью применима всегда, поэтому наша формула (1) будет работать бесконечно, блокируя доступ к остальным формулам. Отсюда вытекает очень важное правило: если в НАМ есть формула с пустой левой частью (→β), то её место – только в самом конце НАМ.

Учтём это правило и перепишем наш НАМ:

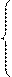
*a (1)

*b (2)

→* (3)

Проверим данный алгоритм:

bbaba → * bbaba baba

Казалось бы, всё в порядке. Однако это не так: наш алгоритм зациклится на пустом входном слове, т.к. постоянно будет применяться формула (3), а согласно условию задачи на таком слове НАМ должен остановиться. В чём причина этой ошибки? Дело в том, что мы ввели знак * для того, чтобы пометить первый символ слова, а затем уничтожить * и этот символ. Но в пустом слове нет ни одного символа, поэтому формулы (1) и (2) ни разу не сработают и постоянно будет выполняться формула (3). Следовательно, чтобы учесть случай пустого входного слова, надо после формул (1) и (2) записать ещё одну формулу, которая уничтожает «одинокую» звёздочку и останавливает алгоритм:

*a (1)

*b (2)

* (3)

→* (4)

Вот теперь мы, наконец-то, составили правильный алгоритм.

1.2 Машина Тьюринга

Была предложена английским математиком Тьюрингом в конце 30-х годов прошлого столетия.

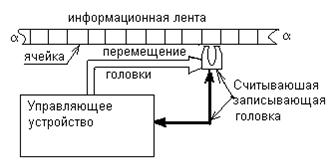
Рисунок 5.1 ― Машина Тьюринга

Машина Тьюринга состоит из информационной ленты, считывающей и записывающей головки и управляющего устройства (рис. 5.1).

Информационная лента бесконечной длины представляет собой последовательность ячеек, в каждую из которых записан в точности только один символ из множества символов алфавита V _t={ a₁, a₂... a_n }. Последовательность символов на ленте формирует слово a =(a₁ a₂... a_|). Пробел между словами также является символом множества V _t. Например, # Î V _t.

С точки зрения формальных грамматик множество символов алфавита V _Т есть множество терминальных символов.

Информационная лента исполняет функции внешней памяти машины Тьюринга.

Считывающая - записывающая головка обозревает одну ячейку информационной ленты, передает информацию о ее содержимом в управляющее устройство, и по указанию последнего сохраняет или изменяет содержимое ячейки.

Управляющее устройство представляет собой механизм, который на каждом шаге вычисления находится в одном из множества состояний Q = { q₁, q₂,... q_m }. В зависимости от состояния q_i и считанного символа a_j управляющее устройство формирует команду на стирание или запись нужного символа в обозреваемую ячейку, перевод управляющего устройства в новое состояние и перемещение головки на соседнюю ячейку информационной ленты. Понятие "состояние" формирует "память машины Тьюринга", т.е. учет всех промежуточных состояний, которые привели машину в текущее состояние q_i. Поэтому множество состояний управляющего устройства называют внутренней памятью машины Тьюринга. С позиции формальных грамматик множество символов состояний управляющего устройства есть множество нетерминальных символов. Среди всех состояний управляющего устройства следует выделить q_o— начальное состояние ("старт") и q_k — конечное состояние, ("стоп"), что облегчит формализацию протоколов машин Тьюринга и их композицию.

Для формализации перемещений головки относительно информационной ленты введем дополнительный алфавит D = { П, Л, С }, где П — означает перемещение головки вправо на одну ячейку информационной ленты, Л — влево на одну ячейку и С — останов.

Работа машины Тьюринга состоит в многократном повторении следующего цикла элементарных действий:

1) считывание символа a_j, находящегося под считывающей головкой;

2) поиск команды, отвечающей текущему состоянию управляющего устройства q_i, и считанному символу a_j, т.е.

q_j a_j => q_| a_m D;

3) исполнение найденной команды, т.е. запись в обозреваемую ячейку символа a_m, перевод управляющего устройства в состояние q_i и перемещение головки на соседнюю ячейку информационной ленты D.

Эти три действия формируют элементарный шаг алгоритмического процесса.

Последовательность команд для реализации процесса вычисления формирует протокол машины Тьюринга или программу алгоритмического процесса.

Следует отметить, что никакие две команды не могут иметь одинаковую пару текущего состояния q_i и считываемого символа a_j, т.е. (q_i a_j). Машина Тьюринга останавливается только в том случае, если на очередном шаге управляющее устройство генерирует состояние q_k Результатом работы машины Тьюринга будет заключительное слово на информационной ленте.

Математическая модель машины Тьюринга имеет вид:

Т =< V_t; Q; D; j; y; x >,

где: VT = { ai; a2;... an }	- символы внешней памяти;
Q = { qo, qi; q2;... qm }	- символы внутренней памяти;
D = { П; Л; С }	- символы перемещения головки;
j: Q Ä Vt => Vt	- функция выхода машины Тьюринга;
y: Q Ä Vt => Q	- функция переходов машины Тьюринга.
x: Q Ä Vt => D	- функция перемещения головки машины Тьюринга.

Описание машины Тьюринга определяется записью всех слов на информационной ленте, положением головки относительно ячеек информационной ленты и текущим состоянием управляющего устройства. Такое описание называют конфигурацией машины Тьюринга:

K = a q_i b,

где a — слово, расположенное слева от головки;

b — слово, расположенное справа от головки;

q_i — текущее состояние машины Тьюринга.

Символ ‘ а_i ’, находящийся в ячейке под считывающей головкой, является первым символом слова b, т.е. b = (a_j g).

К незаключительной конфигурации может быть применима только одна команда, которая переводит машину в новую конфигурацию. Так реализуется дискретность и детерминизм алгоритмического процесса.

Для удобства анализа вычислительных алгоритмов математик Пост предложил ограничить множество символов внешнего алфавита V_t двумя символами, т.е. V_t = {|; #}, где "|" (палочка) есть символ унарного кода числа, а "#" (диеза или решетка) есть символ пробела между числами. При этом любое целое положительное число может быть представлено на информационной ленте последовательностью палочек, как это представлено в табл. 5.1.

Таблица 5.1

Число в десятичной системе счисления	"Слово" в унарном коде на информационной ленте
	| =1^о
	||=1^1+1
	=1^2+1
i	... |=1^i+1

Для упорядочения составления протоколов информационную ленту ограничивают только в одну сторону, т. е. существуют левые и правые полуленты. В зависимости от используемой полуленты приняты различные схемы записи конфигураций машины Тьюринга (табл. 5.2).

Таблица 5.2

Стандартная	Информационная полулента
конфигурация	правая	левая
Начальная	qn|^x 1+1# |^x 2+ 1#...#|^x n+ 1	|^x 1+1# |^x 2+ 1#...#|^x nqn|
Конечная	qk|^y + 1	|^yqk|

Работу машины Тьюринга удобно представлять протоколом, таблицей и графом.

При протокольной записи все команды должны быть записаны упорядоченным списком. На заключительном шаге должно быть получено значение заданной функции, т. е. y = f(x₁, x₂,...x_n).

Например,

1) q_na_i —>q_ia_jD;

2) q_ia_k — > q_ja_iD;

.................................

n) q_|a_m— > q_ka_nC.

При табличном описании каждая строка имеет имя текущего состояния машины, а столбец–имя символа внешней памяти. Тогда элементами таблицы являются правые части команд (q_ja_iD).

Таблица 5.3

	Текущее	Символы vt
	состояние	аi	ак	...	am
	qn	qiajD	...
	qi	...	qjaiD		...
	...	...	...	...	...
	qi	...	...	...	qkanC

Табличная форма описания машины более компактна и позволяет применить матричные методы анализа для оптимизации структуры алгоритма.

При графовом представлении вершинами графа являются состояния машины Тьюринга, а дугами — переходы в те состояния, которые предусмотрены командой. При этом на дуге указывают считываемый символ /записываемый символы в обозреваемой ячейке и команда на перемещение головки (рис. 5.2). Граф машины Тьюринга, реализующей заданный алгоритм, часто называют граф-схемой алгоритма (ГСА).

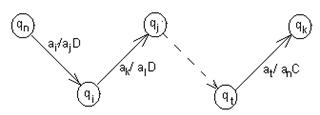
Рисунок 5.2 ― Граф-схема машины Тьюринга

Пример 1 машины Тьюринга. T₂:= базовая функция С_n=1 на правой полуленте:

T₂: q_о|^{x + 1}#®q_k||#;

Протокол T2. 1) qо|®q1# П; 2) q1|®q1# П; 3) q1#®q2# |Л; 4) q2 #®qk|C.	Текущее	Символы vt
состояние		#
qо	q1 #П	—
q1	q1 #П	Q2 |Л
q2	—	q1 |C

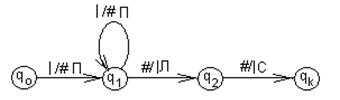
Рисунок 5.3 ― Граф алгоритма базовой функции С_n=1

Пример 2 машины Тьюринга. T₄:= базовая функция I_m,n на правой полуленте:

T₄: q_o|₁^x1+1 # |₂^x2+1 #...#|_m^xm+1#...#|_n^xn+1#®q_k|^xm+1#,

где |_i - слово на i-м месте информационной ленты,

|^xi+1 – число “палочек”.

Чтобы найти на информационной ленте i-е слово, следует установить счетчик |_m, указывающий место слова |_m^xm+1 в последовательности слов.

T₄: q_o|_m #|₁^x1+1#|₂^x2+1#...#|_m^xm+1#|_n^xn+1 ® q_k|_m^xm+1.

Текущее	Символы vt
состояние	|	#	)
qo	q1 #П	-	-
q1	q1 |П	q2)П	-
q2	q2 #П	q3 )Л	-
q3	-	q3 #Л	q4 )Л
q4	q4 |Л	q5 # П	-
q5	q6 #П	-	q8 #П
q6	q6 |П	-	q7 )П
q7	-	q7 #П	q2 #П
q8	-	q8 #П	q9 #П
q9	q9 |П	q10 #П	-
q10	q10 #П	q11 #П	-
q11	q10 #П	q12 #Л	-
q12	q13 |Л	q12 #Л	-
q13	q13 |Л	q14 #П	-
q14	qk |C	-	-

На рис. 5.4 приведен граф, реализующий базовую функцию I_m,n.

Это позволит при каждом проходе вправо, отмечая один символ в слове |_m, удалять очередное слово |_m-1, предшествующее |_m^xi+1.

Для организации вычисления такой функции необходимо увеличить число символов алфавита внешней памяти, что позволит уменьшить число состояний управляющего устройства и упорядочить весь процесс вычисления.

Пусть V_т = {|, #, (}. Считывающая головка находится под первым символом слова счетчика |_m.

При подаче команды “старт” стирается первый символ слова |_m и начинается перемещение головки вправо.

После прочтения всех символов слова |_m по команде q₁#®q₂) П ставится скобка, закрывающая оставшиеся символы слова |_m, и головка перемещается на слово |^x1+1.

По команде q₂| ®q₂#П стираются все символы слова |₁^x1+1 и ставится закрывающая скобка q₂#®q₃)Л. Начинается перемещение считывающей головки влево за очередным символом слова |_m-2.

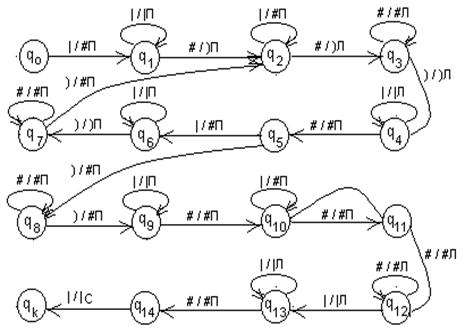
Рисунок 5.4 ― Граф базовой функции I_m,n

Так организован цикл. Затем управляющее устройство стирает второе слово, третье и т. д. пока есть символы “|” в счетчике.

После стирания всех символов в счетчике по команде q₅)®q₈#П головка стирает закрывающую скобку, пробегает все пробелы “#”, по команде q₈)®q₉#П фиксирует место слова |_m^xm+1, пробегает все символы слова |_m^xm+1 и продолжает удалять все слова справа от слова |_m^xm+1по командам q₁₀|®q₁₀#П и q₁₁|®q₁₀#П. Если при чтении ленты в соседних ячейках будут символы “#”, то конец и головка возвращается на первый символ слова |_m^xm+1 по командам: q₁₁#®q₁₂#Л, q₁₂#®q₁₂#Л, q₁₂|®q₁₃|Л, q₁₃|®q₁₃|Л, q₁₃#®q₁₄#П и q₁₄|®q_k|C.

Пример 3 машины Тьюринга. T₆ копирование m раз слово |^x+1 на правой полуленте:

T₆: q_о|^x+1# ® q_k|₁^{x +1}#|₂^x+1 #..#|_m^x+1#.

Для того, чтобы выполнить m копий, необходимо занести на информационную ленту счетчик., т.е. изменить начальную конфигурацию машины, определяющий число копий |_m:

T₆: q_о|_m #|^x+1# ® q_k|₁^{x +1} # |₂^x+1 #..#|_m^x+1#.

При каждом проходе вправо в слове |_m удаляется один символ, затем выполняется обычное копирование слова |^x+1, маркируя каждый переносимый символ командой q₂|®q₃(П и закрывая слово |^x+1 командой q₃#®q₄(П. После переноса всех символов слова |^{x +1} головка возвращается на самый левый символ слова |_m и стирает его.

Пусть V_т.={|, #, (,)}.

Текущее	Символы vt
состояние	|	#	(	)
qо	q1 #П	-	-	q8 #П
q1	q1 |П	q2)П	-	q2)П
q2	q3 (П	-	q2)П	q2)П
q3	q3 |П	q4)П	-	q4)П
q4	q4 |П	q5 |Л	-	-
q5	q5 |Л	-	q6 (П	q5)Л
q6	q3 (П	-	-	q7)Л
q7	q7 |Л	q7 #П	q7 (Л	q7)Л
q8	q9 |Л	-	q8 (П	q8 )П
q9	qk |C	q9 #П	q9 |Л	q9 #Л

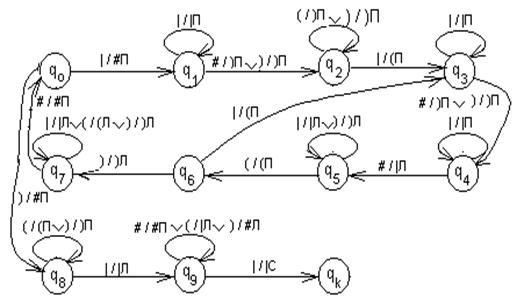
Рисунок 5.5 ― Граф алгоритма тиражирования слова |^x+1

Процесс продолжается до тех пор, пока не будут удалены все символы в слове 1_m. После этого следует удалить все вспомогательные символы "("и")" и поставить головку машины в начало первого слова |^x+1 . Множество команд представлены таблицей, а работа машины показана графом на рис. 5.5.

2 Примеры задач

1. Вычисление произведения двух чисел в унарном коде.

2. Выделить типовые машины Тьюринга, реализующие элементарные служебные и базовые функции.

q_н|^x # |^y # |^z # |^s # |^t Þ q_k|^(y¸z) # |^(x+t)

Для каждой машины Тьюринга составить таблицу поведения и нарисовать граф. Усеченное вычитание» выполнить для x>y>z>s>t и x<y<z<s<t.

3 Задание

Для выбранной в соответствии с вариантом задания задачи (две части):

1) Разработать протокол нормального алгоритма Маркова.

2) Разработать граф-схему нормального алгоритма Маркова.

3) Отладить протокол с помощью эмулятора машины Маркова.

4) Разработать протокол, таблицу переходов и граф состояний машины Тьюринга с правой полулентой.

5) Отладить протокол с помощью эмулятора машины Тьюринга.

6) Сделать выводы.

4 Содержание отчета

1) Условие задачи в соответствии с вариантом.

2) Определение понятия «Нормальный алгоритм Маркова».

3) Протокол нормального алгоритма Маркова, решающего задачу.

4) Граф-схема нормального алгоритма Маркова, решающего задачу.

5) Математическая модель машины Тьюринга.

6) Протокол машины Тьюринга, решающей задачу.

7) Таблица переходов машины Тьюринга, решающей задачу.

8) Граф состояний машины Тьюринга, решающей задачу.

9) Результаты отладки машины Тьюринга на эмуляторе.

10) Анализ результатов и выводы.

5 Варианты задания

Ниже даны варианты задания, состоящего из двух частей. Первая часть – условие задачи, которая должна быть решена нормальным алгоритмом Маркова. Вторая часть – условие задачи, которая должна быть решена машиной Тьюринга.

Первая часть задания.

1. A = { f,h,p }. В слове P заменить все пары ph на f.

2. A = { f,h,p }. В слове P заменить на f только первую пару ph, если такая есть.

3. A = { a,b,c }. Приписать слово bac слева к слову P.

4. A = { a,b,c }. Заменить слово P на пустое слово, т.е. удалить из P все символы.

5. A={ a,b,c }. Заменить любое входное слово на слово a.

6. Записать нормальный алгоритм, не меняющий входное слово (при любом алфавите A).

7. A={ a,b,c }. Определить, входит ли символ a в слово P. Ответ (выходное слово): слово a, если входит, или пустое слово, если не входит.

8. A={ a,b }. Если в слово P входит больше символов a, чем символов b, то в качестве ответа выдать слово из одного символа a, если в P равное количество a и b, то в качестве ответа выдать пустое слово, а иначе выдать ответ b.

9. A={ 0,1,2,3 }. Преобразовать слово P так, чтобы сначала шли все чётные цифры (0 и 2), а затем – все нечётные.

10. A={ a,b,c }. Преобразовать слово P так, чтобы сначала шли все символы a, затем – все символы b и в конце – все символы c.

11. A={ a,b,c }. Определить, из скольких различных символов составлено слово P; ответ получить в единичной системе счисления (например: acaac → | |).

12. A={ a,b,c }. В непустом слове P удвоить первый символ, т.е. приписать этот символ слева к P.

13. A={ a,b,c }. За первым символом непустого слова P вставить символ c.

14. A={ a,b,c }. Из слова P удалить второй символ, если такой есть.

15. A={ a,b,c }. Если в слове P не менее двух символов, то переставить два первых символа.

16. A={ 0,1,2 }. Считая непустое слово P записью троичного числа, удалить из этой записи все незначащие нули.

17. A={ a,b, c}. Приписать слово abc справа к слову P.

18. A={ a,b,c }. Удалить из непустого слова P его последний символ.

19. A={a,b,c}. Удвоить каждый символ в слове P (например: bacb → bbaaccbb).

20. A={ a,b }. Приписать справа к слову P столько палочек, сколько всего символов входит в P (например: babb → babb|).

21. A={ a,b }. Приписать справа к слову P столько палочек, со скольких подряд идущих символов a начинается это слово (например: aababa → aababa| |).

22. A={ a,b,c }. Удалить из слова P второе вхождение символа a, если такое есть.

23. A={ a,b,c }. Удалить из слова P третье вхождение символа a, если такое есть.

24. A={ a,b,c }. Оставить в слове P только первое вхождение символа a, если такое есть.

25. A={ a,b,c }. В непустом слове P оставить только последний символ.

26. A={ a,b,c }. Из всех вхождений символа a в слово P оставить только последнее вхождение, если такое есть.

27. A={ a,b,c }. Если слово P начинается с символа a, то заменить P на пустое слово, а иначе P не менять.

28. A={ a,b }. Если слово P содержит одновременно символы a и b, то заменить P на пустое слово.

29. A={ a,b,c }. Если буквы в непустом слове P не упорядочены по алфавиту, то заменить P на пустое слово, а иначе P не менять.

30. A={ a,b,c }. Если P отлично от слова abaca, то заменить его на пустое слово.

31. A={ a,b,c }. Определить, входит ли первый символ непустого слова P ещё раз в это слово. Ответ: слово a, если входит, или пустое слово иначе.

32. A={ a,b }. Перенести первый символ непустого слова P в конец слова.

33. A={ a,b }. Перенести последний символ непустого слова P в начало слова.

34. A={ a,b }. В непустом слове P переставить первый и последний символы.

35. A={ a,b }. Если в непустом слове P совпадают первый и последний символы, то удалить оба этих символа, а иначе слово не менять.

36. A={ a,b }. Определить, является ли слово P палиндромом (перевёртышем, симметричным словом). Ответ: слово a, если является, или пустое слово иначе.

37. A={ a,b }. Пусть слово P имеет нечётную длину. Удалить из него средний символ.

38. A={(,)}. Определить, сбалансировано ли слово P по круглым скобкам.

Ответ: Д (да) или Н (нет)

39.А={ a,b }. Перевернуть слово P (например: abb → bba).

Вторая часть задания.

1. A={a,b,c}. Приписать слева к слову P символ b (P → bP).

2. A={a,b,c}. Приписать справа к слову P символы bc (P → Pbc).

3. A={a,b,c}. Заменить на a каждый второй символ в слове P.

4. A={ a,b,c }. Оставить в слове P только первый символ (пустое слово не

менять).

5. A={ a,b,c }. Оставить в слове P только последний символ (пустое слово не менять).

6. A={ a,b,c }. Определить, является ли P словом ab. Ответ (выходное слово): слово ab, если является, или пустое слово иначе.

7. A={ a,b,c }. Определить, входит ли в слово P символ a. Ответ: слово из одного символа a (да, входит) или пустое слово (нет).

8. A={ a,b,c }. Если в слово P не входит символ a, то заменить в P все символы b на с, иначе в качестве ответа выдать слово из одного символа a.

9. A={ a,b,c }. Приписать слева к непустому слову P его первый символ.

10. A={ a,b }. Для непустого слова P определить, входит ли в него ещё раз его первый символ. Ответ: a (да) или пустое слово.

11. A={ a,b }. В непустом слове P поменять местами его первый и последний символы.

12. A={ a,b }. Определить, является P палиндромом (перевёртышем, симметричным словом) или нет. Ответ: a (да) или пустое слово.

13. A={ a,b }. Заменить в P каждое вхождение a на bb.

14. A={ a,b,c }. Заменить в P каждое вхождение ab на c.

15. A={ a,b }. Удвоить слово P (например: abb → abbabb).

16. A={ a,b }. Удвоить каждый символ слова P (например: bab → bbaabb).

17. A={ a,b }. Перевернуть слово P (например: abb → bba).

6 Список литературы

1) Пильщиков В.Н., Абрамов В.Г., Вылиток А.А., Горячая И.В. Машина Тьюринга и алгоритмы Маркова. Решение задач. (Учебно-методическое пособие) - М.: МГУ, 2006. – 47 с.

2) Пономарев В.Ф. Дискретная математика для инженеров.- Калининград: ФГОУ ВПО КГТУ, 2010.- 351 с.

Дата добавления: 2014-10-31