Расчет плотности (G) графа G

Рассчитаем плотность графа G, т.е. наибольшее число вершин подграфа графа G, между всеми вершинами которого задано отношение смежности.

Получим матрицы смежности ||H|| и достижимости ||Q|| графа G (рисунок 6.10).

H

Q

Рисунок 6.10 ― Матрицы ||H|| и ||Q|| графа G

В матрице | | Q|| сформируем блоки, используя метод визуального анализа и перестановок строк (т.е. стоки меняются местами) и перестановок столбцов (т.е. столбцы меняются местами). В итоге получим матрицу ||Q|| на рисунке 6.11.

Q

Рисунок 6.11 ― Матрица || Q || с тремя выделенными блоками

Анализ матрицы || Q || на рисунке 6.11 показывает, что поскольку число блоков равно трем, то имеем три полных подграфа G с тремя вершинами в каждом (1-ый блок: 3х3, 2-ой блок: 3х3, 3-ий блок: 2х2). Иными словами, |Х`<sub>1</sub>|=3, |Х`₂|=3, |Х`₃|=2 (рисунок 6.12).

Рисунок 6.12 ― Три подграфа графа G

Обозначения: пунктиром выделены полные подграфы графа G.

Таким образом имеем:

.

Расчет неплотности ε(G) графа G

Рассмотрим плотность графа G, т.е. наибольшее число вершин пустого подграфа графа G между всеми вершинами которого нет отношений смежности.

Построим обратный граф ┐ G для графа G. Для этого получим матрицу || H || и обратную ей матрицу || ┐ H || (рисунок 6.13).

H

┐ H

Рисунок 6.13 ― Матрицы смежности (слева-направо) графа G и графа ┐ G

Строим матрицу достижимости графа ┐ G и выполняем операцию перестановки строк и столбцов. Результаты показаны на рисунке 6.14.

┐ Q^p

┐ Q^p

Рисунок 6.14 ― Матрицы достижимости ┐ Q^p графа ┐ G

Примечание: матрица на рисунке справа имеет блочную структуру.

На рисунке 6.15 показан обратный граф ┐ G.

Рисунок 6.15 - Обратный граф ┐ G

Анализ матрицы ┐ Q^p с блочной структурой на рисунке 6.14 показывает, что поскольку число блоков – три, то имеем три пустых подграфа графа G (рисунок 6.16):

|Х`<sub>1</sub>|=3, |Х`₂|=3, |Х`₃|=2.

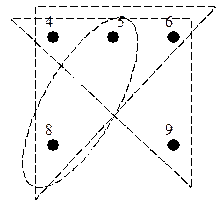Рисунок 6.16 - Три пустых подграфа графа G

Таким образом имеем:

.

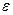
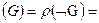
Расчет внешней устойчивости ψ(G) графа G

Рассчитаем внешнюю устойчивость графа G, т.е. наименьшее число вершин графа G смежных со всеми остальными вершинами графа.

Составим таблицу 6.2 отображений для графа G и дополним ее столбцом несмежных вершин.

Таблица 6.2 ― Таблица отображений графа G

xi	Hi	┐ Hi
	5,7	6,8,9
	4,6,7	8,9
	5,7	4,8,9
	4,5,6,8,9
	7,9	4,5,6
	7,8	4,5,6

Анализ таблицы 6.2 показывает, что в столбце ┐ H_i есть несмежные вершины. В этом случае необходимо построить еще одну таблицу – таблицу 6.3 следующим образом.

Таблица 6.3 строится на базе строк таблицы 6.2, в которых нет знака в столбце ┐ H_i. В нашем случае таких строк – пять. В строках первого столбца таблицы 6.3 пары вершин, образованные полным перебором вершин из первого и второго столбцов таблицы 6.2. В строках второго и третьего столбцов таблицы 6.3 указываются смежные и несмежные вершины, соответственно, для {х_i,х_j}, перечисляемых в строках первого столбца таблицы 6.3.

Таблица 6.3 ― Таблица отображений и несмежных вершин для двухэлементных подмножеств

{xi,xj}	H(xi,xj)	┐H(xi,xj)
x4,x5	x6,x7	x8,x9
x4,x7	x5,x6,x8,x9
x5,x6	x4x7	x8,x9
x5,x7	x4,x6,x8,x9
x7,x6	x5,x8,x9	x4
x7,x8	x4,x5,x6,x9
x7,x9	x4,x5,x6,x8
x8,x9	x7	x4,x5,x6

Если в таблице 6.3 найдется 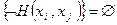, т.е. хотя бы в одной строке столбца 3 таблицы 6.3 будет стоять знак , то расчеты завершены. В противном случае необходимо перейти к формированию новых таблиц отображений и несмежных вершин для трех элементных подмножеств 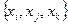, т.е. H(x_i,x_j,x_k) и ┐ H(x_i,x_j,x_k) и т.д.

В нашем примере во второй, четвертой, шестой и седьмой строках стоят знаки . Значит расчеты закончены и можно приступать к анализу таблицы 6.2 и таблицы 6.3.

По итогам анализа таблицы 6.3 можно сформировать множество T потенциальных ядер графа G, т.е.

Т= {{ x₄,x₅},{ x₄,x₇},{x₇,x₈},{x₇, x₄}},

где T₁={ x₄,x₅}, T₂={x₅,x₇}, T₃={x₇,x₈}, T₄={x_7, x₄}.

Тогда ψ(G)={| |}=||}|_i=1;4=2.

Дата добавления: 2014-10-31