Тема: чисельне інтегрування, квадратурні формули

Лабораторна робота 15.

(2г.)

Мета: Отримати відомості проквадратурні формули, чисельні методи інтегрування

та навчитися застосовувати ці методи до конкретних задач.

Теоретичні відомості.

Якщо функція f (х) неперервна на відрізку [a; b] і відома її первісна F, то справедлива формула Ньютона – Лейбниця . Проте цією формулою неможливо скористатися, якщо первісну F не можна виразити у відомих (традиційно в елементарних) функціях, або якщо функцію f задано таблично або графічно. У цих випадках необхідно будувати методи для наближеного обчислення визначених інтегралів. Найчастіше застосовують квадратурні формули.

Означення. Квадратурні формули – це формули вигляду 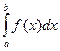≈ 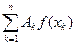. Суму в правій частині формули 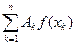називають квадратурною сумою, числа х_k і А_k називають відповідно вузлами і коефіцієнтами квадратурної формули.

Найпростіші квадратурні формули можна отримати з наочних міркувань. Наприклад,

нехай функція f (х) близька до лінійної. Тоді природно замінити інтеграл площею трапеції з висотою b – a та основами f (a) і f (b).

f (a)

f (b)

a b

Рисунок 1

В результаті отримаємо формулу трапецій:

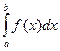≈ (b – a) .

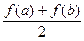Більш складні квадратурні формули отримують за допомогою апарату інтерполювання. Наприклад, саме так отримана квадратурна формула

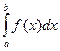≈ (f (a) + 4 f () + f (b)),

яку називають квадратурною формулою Сімпсона.

Якщо функцію f (х) задано на великому проміжку [a; b], то точність розглянутих квадратурних формул стає неприйнятною. Тому для обчислення 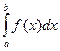застосовують відповідну узагальнену квадратурну формулу. Це означає, що відрізок [a; b] ділять на рівні відрізки і на кожному з них застосовують дану квадратурну формулу. Наприклад, узагальнена формула трапецій виглядає так:

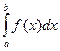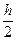≈ (f (a) + 2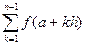+ f (b)). (1)

А узагальнена формула Сімпсона має вигляд

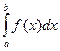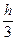≈ (f (a) + 4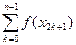+ 2+ f (b)). (2)

Хід роботи.

Задача 1. Обчислити наближені значення інтегралу функції f (x) = e^{sin x} cos2x на відрізку [0;1] за узагальненою формулою трапецій з кроками інтегрування h = 0,2 0,1 0,05.

Розв’язання. Спочатку побудуємо електронну таблицю значень функції f (x) у вузлах інтегрування. Надамо чарункам електронної таблиці таких значень:

	A	B
	x	f (x)
		= EXP(SIN(A2))*COS(2*A2)
	= A2 + h	↓
	↓	↓

Символ ↓ означає копіювання попередніх чарунок. Спочатку h = 0,2 і треба копіювати у стовпці А до значення 1, тобто до чарунки А7. В результаті отримаємо таку таблицю:

	A	B
	х	f (x)
	0,2	1,12349
	0,4	1,028424
	0,6	0,637322
	0,8	-0,05983
		-0,96537

У стовпці С до отриманої таблиці додамо відповідні коефіцієнти узагальненої формули трапецій:

	A	B	С
	х	f (x)	к
	0,2	1,12349
	0,4	1,028424
	0,6	0,637322
	0,8	-0,05983
		-0,96537

Аналогічно дістанемо такі таблиці для h = 0,1 і h = 0,05:

	E	F	G
	х	f (x)	к
	0,1	1,082961
	0,2	1,12349
	0,3	1,109107
	0,4	1,028424
	0,5	0,872667
	0,6	0,637322
	0,7	0,323702
	0,8	-0,05983
	0,9	-0,49729
		-0,96537

	J	K	L
	х	f (x)	к
	0,05	1,045997
	0,1	1,082961
	0,15	1,109319
	0,2	1,12349
	0,25	1,123917
	…	…	…
	0,75	0,139856
	0,8	-0,05983
	0,85	-0,27311
	0,9	-0,49729
	0,95	-0,72921
		-0,96537

На основі цих обчислень побудуємо таблицю для отримання відповідних наближень інтегралу функції f (x) = e^{sin x} cos2x.

	A	B	C
	h	s	I
	0,2	= СУММПРОИЗВ(B2:B7;C2:C7)	= 0,5*A26*B26
	0,1	= СУММПРОИЗВ(F2:F12;G2:G12)	↓
	0,05	= СУММПРОИЗВ(K2:K22;L2:L22)	↓

Тут у стовпці А крок інтегрування h. У стовпці В інтегральна сума, у стовпці С – відповідне наближене значення інтеграла згідно з узагальненою формулою трапецій (1).

В результаті отримаємо таку таблицю:

	A	B	C
	h	s	I
	0,2	5,493444	0,549344
	0,1	11,27574	0,563787
	0,05	22,69522	0,567381

Задача 2. Обчислити наближені значення функції f (x) = e^xsinx на відрізку [0;1] за узагальненою формулою Сімпсона з кроками інтегрування h = 0,5 0,25 0,125.

Розв’язання. Зауважимо, що кроки інтегрування h = 0,5 0,25 0,125 є найменшими можливими оскільки за узагальненою формулою Сімпсона (2) кількість відрізків m = 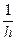, на які вузли інтегрування ділять [0;1], обов’язково є парним. Надамо таких значень чарункам електронної таблиці:

	A	B
	x	f (x)
		= EXP(A2)*SIN(A2)
	= A2 + h	↓
	↓	↓

В результаті, наприклад, при h = 0,125 отримаємо таку таблицю:

	A	B
	х	f (x)
	0,125	0,141275
	0,25	0,317673
	0,375	0,532923
	0,5	0,790439
	0,625	1,093106
	0,75	1,443029
	0,875	1,841241
		2,287355

У стовпці С до отриманої таблиці додамо відповідні коефіцієнти узагальненої формули Сімпсона (2):

	J	K	L
	х	f (x)	к
	0,125	0,141275
	0,25	0,317673
	0,375	0,532923
	0,5	0,790439
	0,625	1,093106
	0,75	1,443029
	0,875	1,841241
		2,287355

Аналогічно з двома іншими таблицями:

	A	B	С
	х	f (x)	к
	0,5	0,790439
		2,287355

	E	F	G
	х	f (x)	к
	0,25	0,317673
	0,5	0,790439
	0,75	1,443029
		2,287355

На основі цих обчислень побудуємо таблицю для отримання відповідних наближень інтегралу функції f (x) = e^{sin x} cos2x, ідентичну таблиці задачі 1:

	A	B	C
	h	s	I
	0,5	= СУММПРОИЗВ(B2:B4;C2:C4)	= А16*B16/3
	0,25	= СУММПРОИЗВ(F2:F6;G2:G6)	↓
	0,125	= СУММПРОИЗВ(K2:K10;L2:L10)	↓

Тут у стовпці С – наближення інтегралу згідно з узагальненою формулою Сімпсона (2).

В результаті отримаємо таку таблицю:

	A	B	C
	h	s	I
	0,5	5,449112	0,908185
	0,25	10,91104	0,909254
	0,125	21,82382	0,909326

Дата добавления: 2014-10-31