
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Неполное общее уравнение плоскости
|
|
|
|
Если все числа А, В, С и D отличны от нуля, то общее уравнение плоскости 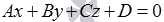 называется полным. В противном случае, общее уравнение плоскости называется неполным.
называется полным. В противном случае, общее уравнение плоскости называется неполным.
Рассмотрим все возможные общие неполные уравнения плоскости в прямоугольной системе координат Oxyz в трехмерном пространстве.
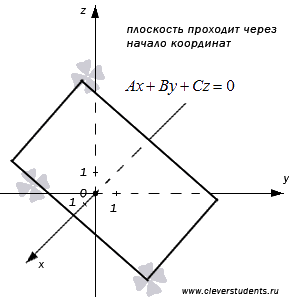
Пусть D = 0, тогда имеем общее неполное уравнение плоскости вида 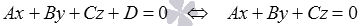 . Эта плоскость в прямоугольной системе координт Oxyz проходит через начало координат. Действительно, при подстановке координат точки
. Эта плоскость в прямоугольной системе координт Oxyz проходит через начало координат. Действительно, при подстановке координат точки 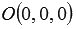 в полученное неполное уравнение плоскости мы приходим к тождеству
в полученное неполное уравнение плоскости мы приходим к тождеству 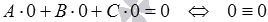 .
.
При 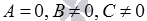 , или
, или 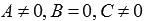 , или
, или 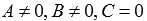 имеем неполные общие уравнения плоскостей
имеем неполные общие уравнения плоскостей 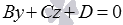 , или
, или  , или
, или  соответственно. Эти плоскости параллельны координатным осям Ox, Oy и Oz соответственно. При D = 0 плоскости проходят через эти координатные оси соответственно. Также можно отметить, что неполные общие уравнения плоскости
соответственно. Эти плоскости параллельны координатным осям Ox, Oy и Oz соответственно. При D = 0 плоскости проходят через эти координатные оси соответственно. Также можно отметить, что неполные общие уравнения плоскости 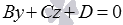 ,
,  и
и  определяют плоскости, перпендикулярные координатным плоскостям Oyz, Oxz и Oxy соответственно.
определяют плоскости, перпендикулярные координатным плоскостям Oyz, Oxz и Oxy соответственно.

При 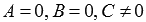 , или
, или 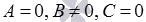 , или
, или 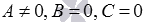 имеем общие неполные уравнения плоскостей
имеем общие неполные уравнения плоскостей  , или
, или  , или
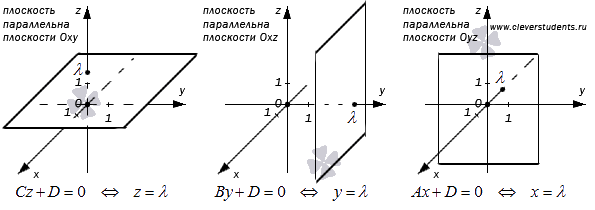
, или  соответственно. Эти уравнения задают плоскости, параллельные координатным плоскостям Oxy, Oxz и Oyz соответственно и проходящие через точки
соответственно. Эти уравнения задают плоскости, параллельные координатным плоскостям Oxy, Oxz и Oyz соответственно и проходящие через точки  и
и  соответственно. При D = 0 получаем уравнения самих координатных плоскостей Oxy, Oxz и Oyz, они имеют вид z = 0, y = 0 и x = 0 соответственно.
соответственно. При D = 0 получаем уравнения самих координатных плоскостей Oxy, Oxz и Oyz, они имеют вид z = 0, y = 0 и x = 0 соответственно.
Разберем решения нескольких примеров на составление неполного уравнения плоскости.
Пример. Напишите общее уравнение плоскости параллельной координатной плоскости Oyz и проходящей через точку  .
.
Решение. Плоскость, которая параллельна координатной плоскости Oyz, может быть задана общим неполным уравнением плоскости вида  . Так как точка
. Так как точка  принадлежит плоскости по условию, то координаты этой точки должны удовлетворять уравнению плоскости
принадлежит плоскости по условию, то координаты этой точки должны удовлетворять уравнению плоскости 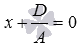 , то есть, должно быть справедливо равенство
, то есть, должно быть справедливо равенство 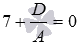 . Отсюда находим
. Отсюда находим  . Таким образом, искомое уравнение имеет вид
. Таким образом, искомое уравнение имеет вид 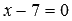 .
.
Второй способ решения этой задачи. Так как плоскость, общее уравнение которой нам требуется составить, параллельна плоскости Oyz, то в качестве ее нормального вектора можно взять нормальный вектор плоскости Oyz. Нормальным вектором координатной плоскости Oyz является координатный вектор 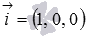 . Теперь мы знаем нормальный вектор плоскости и точку плоскости, следовательно, можем записать ее общее уравнение:
. Теперь мы знаем нормальный вектор плоскости и точку плоскости, следовательно, можем записать ее общее уравнение:
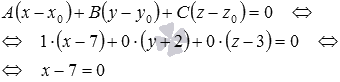
Ответ. 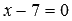
Пример. Составьте общее уравнение плоскости, которая перпендикулярна координатной плоскости Oxy, проходит через начало координат и точку 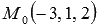 .
.
Решение. Плоскость, перпендикулярная координатной плоскости Oxy описывается общим неполным уравнением плоскости вида  . Так как по условию плоскость проходит через начало координат, то D = 0, следовательно, уравнение плоскости примет вид
. Так как по условию плоскость проходит через начало координат, то D = 0, следовательно, уравнение плоскости примет вид 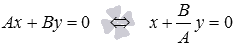 . Осталось найти значение
. Осталось найти значение 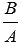 . Из условия нам известно, что плоскость проходит через точку
. Из условия нам известно, что плоскость проходит через точку 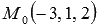 , тогда ее координаты должны удовлетворять уравнению плоскости. Следовательно, справедливо равенство
, тогда ее координаты должны удовлетворять уравнению плоскости. Следовательно, справедливо равенство 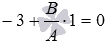 , откуда находим
, откуда находим 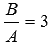 . Теперь мы можем написать искомое общее уравнение плоскости, оно имеет вид
. Теперь мы можем написать искомое общее уравнение плоскости, оно имеет вид 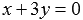 .
.
Ответ. 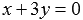
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 1605; Нарушение авторских прав?; Мы поможем в написании вашей работы!