Покажем два способа ее решения

Нахождение уравнения плоскости, проходящей через три заданные точки.

Уравнение плоскости, которая проходит через три заданные точки, не лежащие на одной прямой.

Прежде чем приступать к составлению уравнения плоскости, проходящей через три заданные точки пространства, вспомним одну аксиому: через три несовпадающие и не лежащие на одной прямой точки трехмерного пространства проходит единственная плоскость. Таким образом, задав три различных и не лежащих на одной прямой точки, мы в трехмерном пространстве однозначно определим плоскость, проходящую через эти точки.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz, в ней заданы три несовпадающие точки 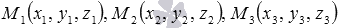, которые не лежат на одной прямой. Поставим перед собой следующую задачу: написать уравнение плоскости, проходящей через эти три точки.

Первый способ составления уравнения плоскости, проходящей через три заданные точки .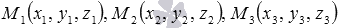

Известно, что общее уравнение плоскости вида 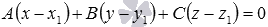задает в прямоугольной системе координат Oxyz плоскость 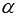, которая проходит через точку 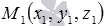, а нормальный вектор плоскости 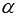имеет координаты 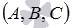. Следовательно, мы можем составить общее уравнение плоскости, если знаем координаты точки, через которую она проходит, и координаты нормального вектора этой плоскости. От этого знания и будем отталкиваться при нахождении уравнения плоскости, проходящей через три заданные точки .

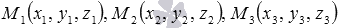Итак, из условия задачи нам известны координаты точки (даже координаты трех точек), через которую проходит плоскость, уравнение которой нам требуется составить. Осталось отыскать координаты нормального вектора 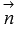этой плоскости.

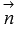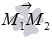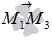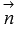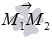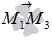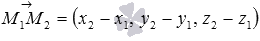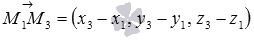Так как нормальный вектор плоскости и любой ненулевой вектор этой плоскости перпендикулярны, то вектор перпендикулярен как вектору , так и вектору . Следовательно, в качестве вектора можно принять векторное произведение векторов и . Так как и , то 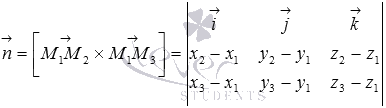. После вычисления записанного определителя, станут видны координаты нормального вектора 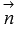, и можно записывать требуемое уравнение плоскости, проходящей через три заданные точки.

Второй способ нахождения уравнения плоскости, проходящей через три заданные точки .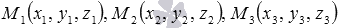

Очевидно, что множество точек 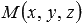определяет в прямоугольной системе координат Oxyz в трехмерном пространстве плоскость, проходящую через три различные и не лежащие на одной прямой точки 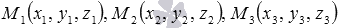, тогда и только тогда, когда три вектора 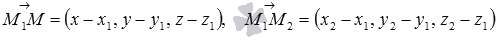и 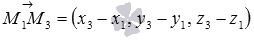компланарны.

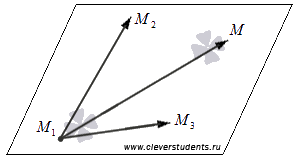
Следовательно, должно выполняться условие компланарности трех векторов 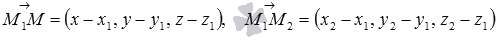и 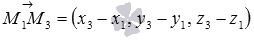, то есть, смешанное произведение векторов 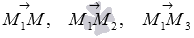должно быть равно нулю: . Это равенство в координатной форме имеет вид 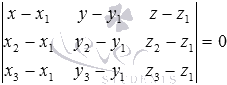. Оно, после вычисления определителя, представляет собой общее уравнение плоскости, проходящей через три заданные точки .

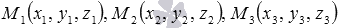Далее, от полученного общего уравнения плоскости, проходящей через три заданные точки, вы при необходимости можете перейти к уравнению плоскости в отрезках или к нормальному уравнению плоскости.

Дата добавления: 2014-10-31