Решение. Воспользуемся первым способом решения.Вычисляем координаты векторов и :

Воспользуемся первым способом решения. Вычисляем координаты векторов 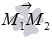и 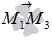: 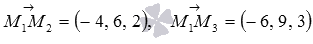. Находим векторное произведение векторов 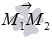и : .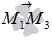

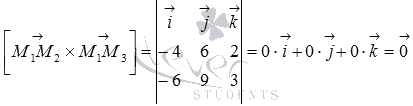Так как 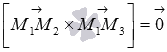, то векторы 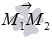и 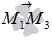коллинеарны, следовательно, заданные точки 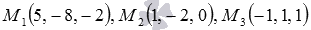лежат на одной прямой. Таким образом, поставленная задача имеет бесконечное множество решений, так как любая плоскость, содержащая прямую, на которой лежат точки М₁, М₂, М₃, является решением задачи.

Если будем решать эту задачу вторым способом, то получим:

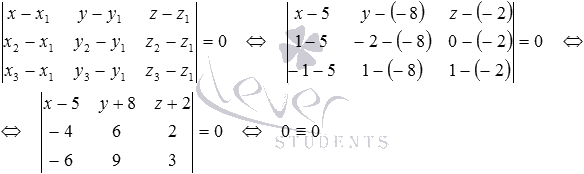
Мы приходим к тождеству, из которого можно заключить, что заданные точки 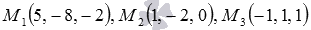лежат на одной прямой.

Если Вам все же захочется написать уравнение какой-нибудь плоскости (из их бесконечного числа), проходящей через три точки 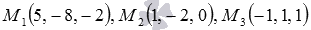, то следует выполнить следующие действия:

· написать уравнения прямой М₁М₂ (прямой М₁М₃ или М₂М₃),

· взять некоторую точку , координаты которой не удовлетворяют уравнениям прямой М₁М₂,

· составить уравнение плоскости, проходящей через три различных и не лежащих на одной прямой точки М₁, М₂ и М₄.

Глава 2. Прямая в пространстве.

Дата добавления: 2014-10-31