Выберите один правильный ответ. ТЕМА 5. Статистические закономерности малых выборок

ТЕМА 5. Статистические закономерности малых выборок. Распределение Стьюдента.

1. Наиболее общую совокупность изучаемых объектов называют:

1) выборочной

2) генеральной

3) репрезентативной.

2. Число объектов совокупности называется:

1) размером

2) величиной

3) объемом.

3. Среднее арифметическое значение признака выборочной совокупности называется:

1) генеральной средней

2) выборочной средней

3) вариантой.

4. Средние арифметические выборочных совокупностей, извлеченных из одной и той же генеральной совокупности:

1) могут иметь разные значения

2) всегда имеют одинаковые значения

3) имеют одинаковые значения, равные среднему арифметическому генеральной совокупности.

5. Среднеквадратическая (стандартная) ошибка характеризует разброс:

1) выборочных средних вокруг генеральной средней

2) вариант вокруг генеральной средней

3) вариант вокруг выборочной средней.

6. Интервал, покрывающий неизвестный параметр с заданной вероятностью, называется:

1) статистическим

2) доверительным

3) классовым.

7. Если признак в генеральной совокупности распределен по нормальному закону, то в выборочной совокупности при числе членов, меньшем 30:

1) признак распределен по нормальному закону

2) о законе распределения признака ничего сказать нельзя

3) признак подчиняется распределению Стьюдента.

8. Известно, что признак в генеральной совокупности распределен по нормальному закону. На основе измерений получены следующие значения признака: 3, 5, 6, 4, 7. Тогда выборочная дисперсия равна:

1) 3,0

2) 1,5

3) 2,5

4) 2,0.

9. Известно, что признак в генеральной совокупности распределен по нормальному закону. D=25, n=4, тогда стандартная ошибка равна:

1) 3,0

2) 1,5

3) 2,5

4) 2,0.

10. Для выборки получены значения: среднее 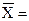5,0; среднеквадратическое отклонение S=1.5; ошибка среднего 0,5. Тогда объем выборки равен:

1) 3

2) 9

3) 5

4) 8.

11. Для выборки получены значения: среднее 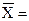5,0; среднеквадратическое отклонение S=1.5; ошибка среднего 0,5. Тогда при q= 0,01 доверительный интервал равен:

1) ±1,7

2) ±1,1

3) ±0,5

4) ±0,2.

12. Случайная величина распределена по нормальному закону. Выборочное среднее равно 4,1; выборочное среднеквадратическое отклонение S=3; n=36; доверительная вероятность Р=0,95. Тогда величина генеральной средней изменяется в пределах:

1) 3,12 £ m £ 5,08

2) 2,36 £ m £ 5,84

3) 3,08 £ m £ 5,12.

13. При сравнении достоверности различия двух зависимых выборок объем контрольной выборки равен 5, объем опытной выборки равен 5. Тогда число степеней свободы для определения табличного значения критерия Стьюдента t_табл. равно:

1) 5

2) 10

3) 8

4) 4.

14. При сравнении достоверности различия средних арифметических двух независимых выборок объем контрольной выборки равен 5, объем опытной выборки равен 5. Тогда число степеней свободы для определения t_табл. равно:

1) 5

2) 10

3) 8

4) 4.

15. Величиной нормированного отклонения t (по Стьюденту) является разность между:

1) выборочной средней и генеральной средней;

2) между выборочной средней и генеральной средней в единицах среднеквадратической ошибки;

3) выборочной и генеральной дисперсией.

16. У группы студентов измерили частоту сердечных сокращений до физической нагрузки и после, полученные выборочные совокупности являются:

1) независимыми

2) зависимыми.

17. У одной группы студентов измерили частоту сердечных сокращений до занятий физкультурой, у второй – после; полученные выборочные совокупности являются:

1) независимыми

2) зависимыми.

18. Совокупность, отобранная из генеральной, называется:

1) выборочной

2) ранжированной.

19. Среднее арифметическое значений признака генеральной совокупности называется:

1) генеральной средней

2) выборочной средней

3) вариантой.

20. Средняя арифметическая величина средних арифметических выборочных совокупностей равна:

1) генеральной средней

2) выборочной средней

3) размеру совокупности.

21. Среднеквадратическая (стандартная) ошибка при увеличении числа вариант в выборке:

1) увеличивается

2) уменьшается

3) не изменяется.

22. Среднеквадратическая (стандартная) ошибка при уменьшении объема числа вариант выборки:

1) увеличивается

2) уменьшается

3) не изменяется.

23. Выборка считается малой, если:

1) n< 100

2) n< 80

3) n< 30.

24. При увеличении доверительной вероятности доверительный интервал:

1) сужается

2) расширяется

3) не изменяется.

25. При увеличении уровня значимости доверительный интервал:

1) сужается

2) расширяется

3) не изменяется.

26. Выборка, характеристики которой соответствуют параметрам генеральной совокупности, называется:

1) достоверной

2) нормальной

3) репрезентативной.

27. Если объем выборки стремится к бесконечности, то среднеквадратическая (стандартная) ошибка стремится к:

1) нулю

2) единице

3) среднеквадратическому отклонению.

Дата добавления: 2014-10-31