УПРАЖНЕНИЯ. Вычислить определенные интегралы

Вычислить определенные интегралы.

Найти площади фигур, ограниченных следующими линиями.

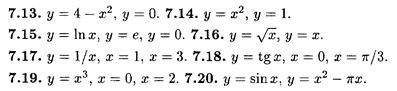
Найти объемы тел, образованных вращением вокруг оси Ох фигуры, ограниченной следующими линиями.

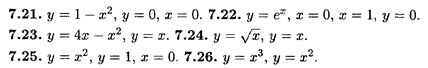
Вычислить несобственные интегралы в случае их сходимости.

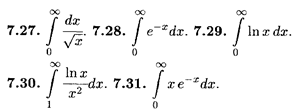
7.32. Найти площадь, заключенную между кривой у = и ее асимптотой при х ≥ 0.

7.33. Найти объем тела, образованного вращением вокруг оси Ох дуги кривой у = e^-x от х = 0 до х = +.

Решить задачи с экономическим содержанием.

7.34. Найти стоимость перевозки М т груза по железной доро­ге на расстояние 1 км при условии, что тариф у перевозки одной тонны убывает на а р. на каждом последующем километре.

7.35. Мощность у потребляемой городом электроэнергии вы­ражается формулой

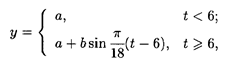
где t — текущее время суток. Найти суточное потребление электроэнергии при а = 15000 кВт, b = 12000 кВт.

Глава 8. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

8.1. Евклидово пространство E^m

Евклидова плоскость и евклидово пространство

Как мы знаем, множество всех упорядоченных пар вещест­венных чисел (x, у) называется координатной плоскостью и каждая точка на ней характеризуется парой своих координат: М(x, у).

Определение 1. Координатная плоскость называется евкли­довой плоскостью, если расстояние между двумя любыми точ­ками M₁(x₁, y₁) и М₂(x₂, y₂) определено по формуле

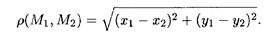
Аналогично вводится и понятие евклидова пространства. В этом случае каждая точка координатного пространства ха­рактеризуется тройкой чисел и тогда расстояние между дву­мя любыми точками пространства M (x₁, y₁,z₁) и М (x₂, y₂, z₂) определяется формулой

Стало быть, евклидова плоскость и евклидово пространст­во определяются способом измерения расстояния между двумя любыми своими точками.

Понятия m-мерного координатного пространства и m-мерного евклидова пространства

Определение 2. Множество всевозможных упорядоченных со­вокупностей т действительных чисел (x₁, х₂, x₃,..., x_m) назы­вается т-мерным координатным пространством А^m.

Каждую упорядоченную совокупность (x₁, x₂, x₃,, …,x_т,) называют точкой этого пространства и обозначают одной буквой М. При этом числа x₁, x₂, x₃, …, x_m называются коорди­натами точки М, что символически записывается следующим образом: М (x₁, x₂,..., x_m).

Определение 3. Координатное пространство А^m называется т-мерным евклидовым пространством Е^m, если между двумя любыми точками М'(х₁', х₂, '..., х_m') и М" (x₁'', х₂'',..., х_m'') про­странства А^m определено расстояние ρ(М', М") по формуле

Очевидно, что введенные понятия m -мерного координат­ного пространства А^m и m -мерного евклидова пространства E^m являются обобщениями понятий соответственно коорди­натных плоскости и пространства и евклидовых плоскости и пространства.

8.2. Множества точек евклидова пространства Е^m

Примеры множеств евклидова пространства Е^m

Будем обозначать символом { М } некоторое множество то­чек m -мерного пространства Е^m. Рассмотрим некоторые при­меры множеств в этом пространстве.

1. Множество { М } всевозможных точек, координаты x₁, x₂,..., x_m которых удовлетворяют неравенству

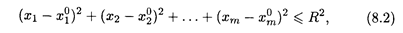
называется т-мерным шаром радиуса R с центром в точке M₀(x,x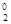,...,x).

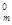Этот пример является m -мерным обобщением соответ­ственно круга на евклидовой плоскости и шара в трехмерном евклидовом пространстве, которые задаются следующими не­равенствами:

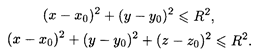
Неравенство (8.2) можно переписать с учетом (8.1) в виде

В случае строгого неравенства ρ(М, М₀) < R множество { М } называется открытым т-мерным шаром. Часто это мно­жество также называют R-окрестностью точки M₀. В случае (8.3) если неравенство не строгое, множество { М } называет­ся замкнутым т-мерным шаром. Эти понятия переносятся на случай любой размерности при т ≥ 2.

2. Множество { М } точек, таких, что расстояние от каж­дой из них до некоторой точки M₀ удовлетворяет равенству ρ(М, М₀) = R, называется т-мерной сферой радиуса R с цент­ром в точке M₀.

Аналогия: для плоскости — окружность (x – x₀)² + (у – y₀)² = R² радиуса R с центром в точке М₀(х₀, у₀), для пространства — сфера (x – x₀)² + (у – y₀)² + (z – z₀)² = R ² радиуса R с центром в точке М₀(х₀, у₀, z₀).

Понятие функции нескольких переменных

Введем понятие функции нескольких переменных.

Определение 1. Пусть каждой точке М из множества точек { М } евклидова пространства E^m по какому-либо закону ста­вится в соответствие некоторое число и из числового множес­тва U. Тогда будем говорить, что на множестве { М } задана функция и = f(M). При этом множества { М } и U называют­ся соответственно областью определения (задания) и областью изменения функции f(M).

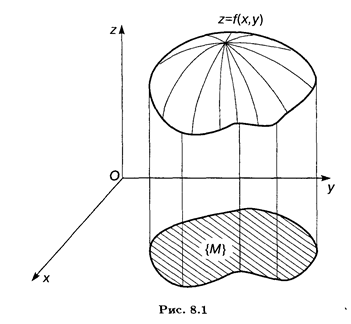
Как известно, функция одной переменной у = f (x) изобра­жается на плоскости в виде линии. В случае двух переменных область определения { М_п } функции z = f(x, y) представляет собой некоторое множество точек на координатной плоскости Оху (рис. 8.1). Координата z называется аппликатой, и тогда сама функция изображается в виде некоторой поверхности в пространстве E³. Аналогичным образом функция от т пере­менных

определенная на множестве { М } евклидова пространства Е^m, представляет собой гиперповерхность в евклидовом простран­стве Е^m+1.

Некоторые виды функций нескольких переменных

Рассмотрим примеры функций нескольких переменных и найдем их области определения.

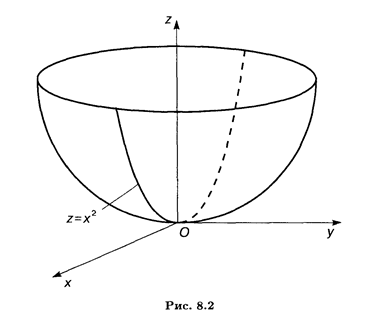
Решение. Это поверхность в евклидовом пространстве Е³. Областью определения этой функции является все множест­во точек плоскости Оху. Область значений этой функции — промежуток [0, ). Данная функция представляет собой пара­болоид вращения (рис. 8.2): в вертикальных сечениях этой поверхности плоскостями Oxz и Оуz получаются соответственно параболы z = х² и z = у².

Решение. Это поверхность в евклидовом пространстве Е³. Область определения данной функции — все множество точек евклидова пространства Е² или плоскости Оху. Эта функция является так называемым эллиптическим конусом с вершиной в начале координат O (0, 0, 0); приведенная формула суммирует две функции, задающие две его симметричные относительно плоскости Оху части (рис. 8.3):

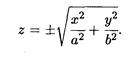
Приведем теперь наиболее часто встречающиеся в различ­ных приложениях виды функций нескольких переменных.

1. Уравнение вида

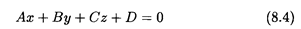
называется общим уравнением плоскости в системе коорди­нат Oxyz. Вектор 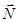= (А, В, С) перпендикулярен плоскости (8.4); он называется нормальным вектором этой плоскости. Ес­ли известно, что плоскость проходит через некоторую точку M₀(x₀, y₀, z₀), то она может быть задана уравнением

Например, составить уравнение плоскости с перпендику­лярным вектором 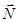= (1, 2, -1), проходящей через точку М ₀ (2, 1, 1), Согласно формуле (8.5) имеем

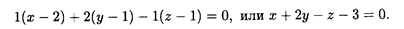
2. Функция Кобба—Дугласа — производственная функция, показывающая объем выпуска продукции Q при затратах ка­питала К и трудовых ресурсов L. Для случая двух переменных она имеет вид

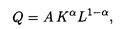
где А > 0 — параметр производительности конкретно взятой технологии, 0 < α < 1 — доля капитала в доходе.

Линии уровня

Понятие линии уровня широко используется прежде всего в геодезии, картографии, при составлении синоптических карт, а также при описании различных физических полей (темпера­тура, давление и пр.).

Определение 2. Линией уровня функции двух переменных z = f(x, y) называется плоская кривая, получаемая при пе­ресечении графика этой функции плоскостью z = С, где С — постоянная величина, параллельной координатной плоскости Оху.

Обычно линии уровня, соответствующие различным зна­чениям постоянной величины С, проецируются на одну плос­кость, например на координатную плоскость Оху; тогда их удобно анализировать и с их помощью исследовать сложный характер поверхности, описываемой функцией z = f (x, у).

Таким образом, можно сказать, что линии уровня функции z = f (x, у) — это семейство кривых на координатной плоскос­ти Оху, описываемое уравнениями вида

Обычно берут арифметическую прогрессию чисел C_i с по­стоянной разностью h; тогда по взаимному расположению ли­ний уровня можно получить представление о форме поверхнос­ти, описываемой функцией z = f(x, у). Там, где функция изме­няется быстрее, линии уровня сгущаются, а там, где поверх­ность пологая, линии уровня располагаются реже (рис. 8.4).

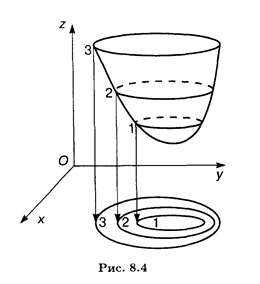
Пример 3. Найти линии уровня функции z = х ² + у ² — 2 х — 2 у.

Решение. Линии уровня данной функции — это семейство кривых на плоскости Оху, описываемое уравнением

Последнее уравнение описывает семейство окружностей с цент­ром в точке O ₁(l, 1) радиуса r = 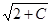. Поверхность враще­ния (параболоид), описываемая данной функцией, становится "круче" по мере ее удаления от оси, которая дается уравнени­ями x = 1, у = 1.

Дата добавления: 2014-10-15