Свойства математического ожидания

Математическое ожидание обладает рядом свойств, кото­рые указаны ниже.

Свойство 1. Математическое ожидание постоянной вели­чины С равно этой постоянной:

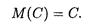
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:

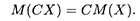
Свойство 3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий:

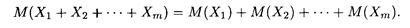
Свойство 4. Математическое ожидание произведения не­зависимых случайных величин равно произведению их мате­матических ожиданий:

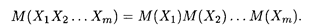
Пример 3. Пусть ежедневные расходы на обслуживание и ре­кламу автомобилей в некотором автосалоне составляют в сред­нем 100 тыс. р., а число продаж Х автомашин в течение дня подчиняется следующему закону распределения:

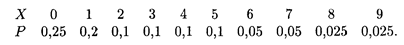
Найти математическое ожидание ежедневной прибыли при це­не на машину 150 тыс. р.

Решение. Ежедневная прибыль подсчитывается по фор­муле

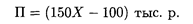
Искомая характеристика М (П) находится с использованием указанных выше свойств математического ожидания (в тыс. р.):

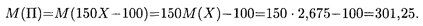
Если в п независимых испытаниях вероятность появле­ния в каждом из них события А постоянна, то ответ на во­прос о среднем числе появления события А дает следующая теорема.

ТЕОРЕМА 1. Математическое ожидание М(Х) числа появ­лений события А в п независимых испытаниях равно произве­дению числа испытаний на вероятность появления события в каждом испытании:

Пример 4. Найти математическое ожидание числа выигрыш­ных лотерейных билетов, если вероятность выигрыша по од­ному билету равна 0,015, причем куплено 200 билетов.

Решение. Поскольку приобретение каждого билета явля­ется независимым испытанием относительно появления собы­тия А — выпадения выигрыша, то здесь применимы теорема 18.1 и формула (18.7). В нашем случае n = 200, р = 0,015, откуда мы получаем

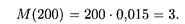
Дата добавления: 2014-10-15