Функция распределения и ее свойства

Непрерывные случайные величины

Пусть Х — непрерывная случайная величина (см. опреде­ление 3 п. 18.1), значения которой сплошь заполняют интервал (а, b). Теперь уже нельзя составить перечень всех возможных значений X, как это было сделано в случае дискретной случай­ной величины. Тем не менее существует способ задания любых видов случайных величин. Пусть х — действительное число. Обозначим вероятность события того, что Х примет значение, меньшее x, через F(x).

Определение 1. Функцией распределения случайной величи­ны Х называется функция F(x), определяющая вероятность того, что Х примет значение, меньшее х:

Геометрический смысл приведенного определения: F(x) — это вероятность того, что случайная величина Х примет зна­чение, изображаемое точкой на числовой оси левее точки х. По виду функции F(x) определяется и вид случайной величины. Уточним понятие непрерывной случайной величины.

Определение 2. Случайная величина называется непрерыв­ной, если ее функция распределения есть непрерывная кусочно-дифференцируемая функция с непрерывной производной.

Таким образом, дискретную случайную величину можно считать кусочно-непрерывной.

Функция распределения обладает рядом фундаментальных свойств, указанных ниже.

Свойство 1. Область значений функции распределения ле­жит на отрезке [0,1]:

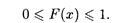
Свойство 2. Функция распределения является неубываю­щей, т.е.

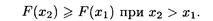
Свойство 3. Если возможные значения случайной вели­чины находятся на интервале (а, b), то F(x) = 0 при х ≤ а и F(x) = 1 при х ≥ b.

Из указанных свойств вытекают важные следствия.

1. Вероятность того, что случайная величина Х принимает значения, заключенные внутри интервала (α, β), равна разнос­ти значений функции распределения на концах этого интервала:

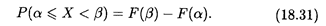
2. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.

3. Если возможные значения непрерывной случайной вели­чины Х расположены на всей числовой оси, то

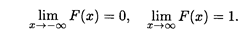
График функции распределения непрерывной случайной ве­личины показан на рис. 18.2.

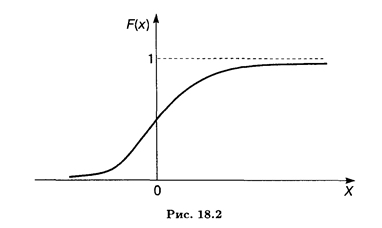
Пример 1. Найти функцию распределения процентного изме­нения стоимости акций по данным примера 3 п. 18.1 и постро­ить ее график.

Решение. Перепишем таблицу распределения дискретной случайной величины в порядке возрастания ее возможных зна­чений:

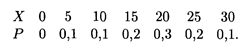
Если х ≤ 5, то F(x) = 0. Если 5 < х ≤ 10, то F(x) = 0,1. На интервале 10 < х ≤ 15 применяем теорему сложения вероят­ностей, так как события Х < 10 и 10 < Х ≤ 15 несовместны: F(x) = 0,1 + 0,1 = 0,2. Аналогично определяются значения F(x) на других интервалах: при 15 < х ≤ 20 F(x) = 0,4; при 20 < х ≤ 25 F(x) = 0,7; при 25 < х ≤ 30 F(x) = 0,9; при х > 30 имеем достоверное событие (все случаи изменения сто­имости акций исчерпаны), т.е. F(x) = 1. Таким образом, иско­мая функция распределения имеет следующую аналитическую форму записи:

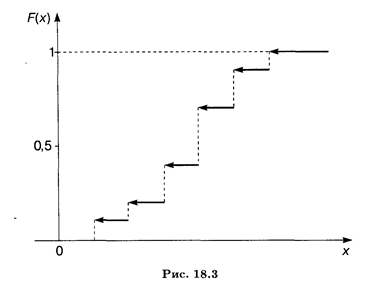
График этой функции распределения показан на рис. 18.3.

Дата добавления: 2014-10-15