Плотность распределения вероятностей и ее свойства

Определение 3. Производная от функции распределения не­прерывной случайной величины Х называется плотностью рас­пределения вероятностей X:

Из этого определения следует, что функция распределения является первообразной для плотности распределения или не­определенным интегралом от нее. Плотность распределения — это "скорость" изменения вероятности Р(Х < х). Из свойства 2 функции распределения следует справедливость следующей фундаментальной теоремы.

ТЕОРЕМА 5. Вероятность того, что непрерывная случай­ная величина Х примет значение на интервале [α, β), опре­деляется по формуле

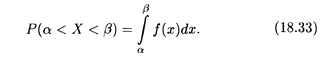
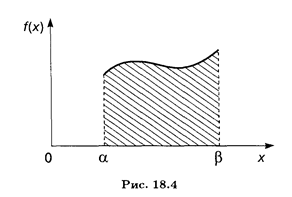
Вспоминая геометрический смысл определенного интеграла (см. п. 7.5), можно сказать, что вероятность того, что непрерывная случайная величина Х примет значение, при­надлежащее интервалу (α, β), равна площади криволинейной трапеции, ограниченной сверху кривой плотности распределе­ния f (x), снизу — осью Ох, а с краев — вертикальными пря­мыми х = α и х = β (рис. 18.4).

Связь между функцией распределения и плотностью рас­пределения вероятностей устанавливается, согласно (18.32), формулой

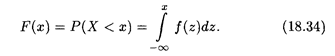
Пример 2. Случайная величина Х задана функцией распре­деления

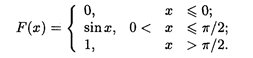
Найти плотность распределения X.

Решение. Функция F(x) является кусочно-дифференциру­емой. Согласно формуле (18.32), дифференцируя F(x) по ин­тервалам ее задания, получаем

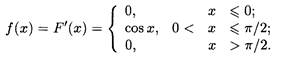
Пример 3. Непрерывная случайная величина Х задана плот­ностью распределения на всей числовой оси:

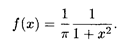
Найти вероятность того, что Х примет значение на интервале (-1, 1).

Решение. Согласно формуле (18.33), искомая вероятность равна

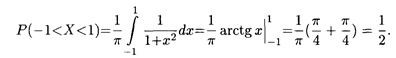
Плотность распределения обладает рядом свойств, основ­ные из них указаны ниже.

Свойство 1. Плотность распределения является неотри­цательной функцией:

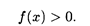
Это следует из характера функции распределения: она являет­ся неубывающей, и, значит, ее производная неотрицательна.

Свойство 2. Несобственный интеграл от плотности рас­пределения в пределах интегрирования по всей числовой оси равен единице:

Это равенство означает достоверность события, что случай­ная величина Х примет значение, принадлежащее интервалу (-,), т.е. вероятность этого события Р (-< Х < ) = 1.

Так, если все возможные значения случайной величины Х лежат внутри интервала (а, b), то

Дата добавления: 2014-10-15