Мгновенная скорость гармонического колебания

V = 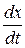= х_мcos(t + _o) (3)

Ускорение: а =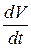= - ²х_мsin(t + _o) = - ²х (4)

Уравнение 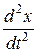+ ²х = 0 (5)

называется дифференциальным уравнением гармонического колебания. Решение этого уравнения приводится к виду (1).

Гармонические колебания происходят под действием силы

F = ma = - m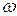²х = - кх, где к = m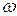², (6)

пропорциональной смещению и направленной к положению равновесия. Ею может быть, например, сила упругости (пружинный маятник). Возвращающие силы могут иметь и иную, не упругую природу. В этих случаях (математический маятник) они называются квазиупругими силами (от латинского quasi – как бы, якобы).

Так как к = m²=, то период гармонического колебания можно вычислить по формуле

T= 2 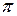(7)

Рассмотрим механическую колебательную систему, называемую математическим маятником.

Математическим маятником называется материальная точка, под- вешенная на невесомой и нерастяжимой нити - рисунок 1.

llll

дддддд

l

Если такой маятник вывести из положения равновесия, то он будет испытывать действие силы, возвращающей его в это положение и равной

F = - mg sin

При малых углах отклонения дугу, описываемую маятником, можно заменить хордой. Тогда

sin = 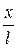, а величина силы

F = - 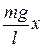= - кх,

т.е. при малых углах отклонения силы, вызывающие колебания, будут пропорциональны смещению, направлены к положению равновесия, и, следовательно, колебания маятника будут гармоническими.

Учитывая, что к = mg/l, то период колебаний математического маятника можно рассчитать по следующей формуле:

T =2 (8)

Из формулы (8) следует, что период колебаний математического маятника зависит от длины маятника l и ускорения силы тяжести g, но не зависит от массы маятника m и амплитуды колебаний x _m

.

ОПИСАНИЕ УСТАНОВКИ И МЕТОДОВ ИЗМЕРЕНИЯ

Определив период колебания математического маятника известной длины, можно рассчитать величину ускорения силы тяжести в данном месте Земли (ускорение силы тяжести зависит от географической широты места) по формуле

g = 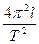( 9)

Математический маятник, применяемый в этой работе, представляет собой массивный шар небольшого радиуса (по сравнению с длиной маятника), подвешенный на двойной нити для того, чтобы колебания происходили возможно более строго в одной плоскости. Расстояние от точки подвеса маятника до пола L = З,20 м, радиус шара R = 3,95 см.

Дата добавления: 2014-10-31