Переключательные функции двух аргументов

Переключательные функции одного аргумента.

Существует четыре различных ПФ одного аргумента, таблица истинности которых имеет следующий вид:

Х	f0(x)	f1(x)	f2(x)	f3(x)

Функция f₀(x) называется константой нуля и обозначается f₀(x)=0 при любом x.

Аналогично функция f₃(x) и называется константа единицы т.е. f₃(x)=1.

Функция f₁(x) повторяет значение аргумента x и следовательно f₁(x)=x.

Функция f₂(x) принимает значение противоположное значению аргумента x. Эту функцию называют отрицанием (инверсией) переменной x и вводят для нее специальное обозначение f₂(x)=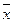. Черта стоящая над аргументом имеет смысл определенного функционального преобразования и называется знаком отрицания.

Логический элемент, реализующий функцию отрицания, называют элементом НЕ или инвертором и по ГОСТу обозначают следующим образом:

Для двух аргументов существует четыре набора значений переменных и шестнадцать различных ПФ.

X1

X2

f0

f1

f2

f3

f4

f5

f6

f7

f8

f9

f10

f11

f12

f13

f14

f15

В шестнадцать ПФ входят также функции, которые зависят от меньшего числа аргументов. Таких функций в таблице истинности шесть:

f₀(x1,x2)=0 – функция константа нуля.

F₁₅(x1,x2)=1 – функция константа единицы.

F₃(x1,x2)=х1,

F₅(x1,x2)=х2,

F₁₂(x1,x2)=,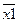

F₁₀(x1,x2)=.

Рассмотрим оставшиеся десять ПФ от двух аргументов.

Функция f₁(x1,x2) называется логическое произведение или конъюнкция и обозначается: f(x1,x2)=х1*х2=х1^х2=х1&х2.

Таблица истинности этой функции совпадает с таблицей умножения двух одноразрядных двоичных чисел т.е. f₁(x1,x2)=1 тогда, когда аргументы равны между собой и равны единице, в остальных случаях функция равна нулю. Логический элемент, реализующий эту функцию, называют элементом И или конъюнктором. Обозначение конъюнктора на функциональных схемах:

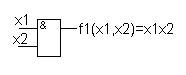
Конъюнкция легко обобщается на случае n аргументов, когда реализуется функция вида: f(x1,x2,…,xn)=x1*x2*…*xn. Функция конъюнкция n аргументов равна единице тогда, когда все аргументы равны единицы.

Функция f7(x1,x2) – называется дизъюнкцией х1 или х2 и обозначается f7(x1,x2)=x1vx2.

Дизъюнкция реализуется элементом, который называется элементом ИЛИ или дизъюнктором.

Сигнал на выходе дизъюнктора принимает нулевое значение только в том случае, если ни один из входных сигналов не имеет в данный момент времени единичное значение.

Функция f9(x1,x2)=x1~x2 – равна единице тогда, когда оба аргумента равны между собой. Это функция носит название логической равнозначности.

Функция f6(x1,x2)=x1x2 – логическая неравнозначность или сумма по модулю 2. эта функция принимает единичное значение тогда, когда х1≠х2. Второе название этой функции объясняется тем, что таблица истинности f6 совпадает с таблицей сложения двух одноразрядных двоичных чисел по модулю 2, т.е. 0+0=0, 1+0=1, 0+1=1, 1+1=0. Обобщим эту функцию на случай n аргументов. Такая функция принимает единичное значение тогда, когда число аргументов равных единице нечетно и равна нулю если число аргументов четно.

Функции f11(x1,x2)=и f13(x1,x2)=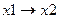называются импликациями и читаются: если х2, то х1 для f11, или если х1, то х2 для f13.

Функция f11 принимает нулевое значение только тогда, когда х2=1, х1=0.

Функция f2(x1,x2)=x1x2 – читается: не верно, что если х1, то х2 и является инверсией функции импликации f13.

.

Функция f13:

.

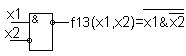Функция f14(x1x2)=x1/x2=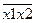называется штрихом Шеффера и является отрицанием функции конъюнкции. Элемент, реализирующий эту функцию, называется элемент И-НЕ и обозначается:

.

f8(x1x2)=x1↓x2=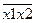. Функция f8 – называется стрелкой Пирса и является отрицанием от дизъюнкции. Элемент, реализующий эту функцию, называется элемент ИЛИ-НЕ и обозначается:

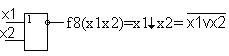
Две последних функции играют очень важную роль в вычислительной технике, поскольку все остальные функции могут быть выражены через каждую из них.

Система ПФ {f1, f2,,…,fm}, из которых с помощью операций суперпозиции и подстановки можно получить любую сколь угодно сложную ПФ, называется функционально полной системой (ФПС) ПФ. Такие системы ПФ называют базисом.

Приведем примеры некоторых базисов:

1. f=x1/x2
2. f=x1↓x2

Первые два базиса называются универсальными. Кроме универсального базиса существует булев базис:

1. f1=x1vx2

f2=x1&x2

f3=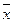

1. f1=x1x2

f2=x1&x2

f3=1 – базис Жигалкина

Возникает вопрос какие ПФ представляют наибольший практический интерес?

Оказывается, что наиболее удобный для решения задач синтеза схем ЭВМ является ФПС ПФ, содержащая операции конъюнкция, дизъюнкция и отрицание, т.е. булев базис. Этот набор ПФ обладает замечательным свойством: может построить любую КС так, что она будет содержать наименьшее количество элементов, в крайнем случае, равное. Поэтому эта система называется основной функционально полной системой ПФ.

Дата добавления: 2014-10-31