Минимизация не полностью определенных переключательных функций

Преобразование функции в минимальную конъюнктивную нормальную форму (КНФ).

Для того, чтобы получить выражение заданной ПФ в форме, содержащей минимальное количество букв, следует, кроме минимальной ДНФ получить также минимальную КНФ и выбрать ту из них, которая содержит меньшее число букв. Существуют различные методы минимизации КНФ. Рассмотрим один из таких методов основанной на минимизации функции 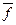и в переходе с помощью формулы де Моргана к функции f. При минимизации 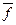можно использовать все методы, которые применялись ранее при нахождении минимальной ДНФ. После получения минимальной ДНФ функции 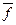с помощью формул де Моргана переходят к минимальной КНФ функции f.

Рассмотрим пример:

Возьмем функцию четырех переменных:

f=v(4,14)

.

В ЭВМ иногда применяются КС, закон функционирования которых определен не полностью. В таких схемах некоторые комбинации сигналов на входы никогда не подаются. Эти комбинации входных сигналов называются запрещенными. Для запрещенных входных комбинаций выходные сигналы не определены, т.е. могут принимать любые значения 0 или 1. Поэтому при синтезе КС с не полностью заданным законом функционирования можно произвольно задать значение выходных сигналов для запрещенной комбинации входных сигналов, поскольку нормальная работа схемы при этом не нарушается. Обычно выходным сигналам на запрещенных комбинациях придают такие значения, при которых можно построить наиболее простую схему. Работа схем с запрещенными комбинациями входных сигналов описывается не полностью определенными ПФ, т.е. функциями, значения которых определены не на всех наборах аргументов. Поэтому минимизация не полностью определенных ПФ с помощью карт Карно сводится к такому до определению ПФ, при котором получаются группы с максимальным числом соседних единиц в каждой группе, а число таких групп минимально. При этом ПФ будет содержать минимум букв.

Пример:

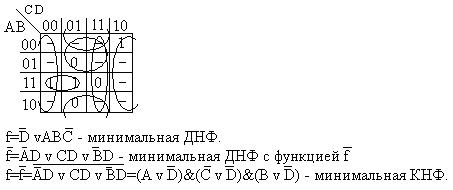
Найти минимальную ДНФ и минимальную КНФ не полностью определенной ПФ от четырех переменных. Функция равна единице на наборах: f=v(2,12,13) и равна нулю на наборах: f=v(5,9,15). На остальных наборах функция не определена.

Дата добавления: 2014-10-31