Кодирование информации

Информацию, поступающую на вход автомата, а так же выходную информацию принято кодировать конечной совокупностью символов. Эту совокупность называют алфавитом, отдельные символы, образующие алфавит – буквами, а любые упорядоченные последовательности букв данного алфавита – словами в этом алфавите.

Например: в алфавите X = (x₁, x₂), состоящем из двух букв, словами будут: x₁, x₂, x₁x₁, x₁x₂, x₂x₁,x₂x₂, x₁x₁x₁ и т.д.

Наряду со словами, состоящими не менее чем из одной буквы, введем слово, не содержащее ни одной буквы, которое будем обозначать символом е и называть пустым словом или пустой буквой.

Математической моделью реального конечного автомата является абстрактный автомат, который имеет один входной канал и один выходной канал.

X(x1,…,xm)

--->

A(a0,...,an)

--->

Y(y1,…,yk)

Автомат функционирует в дискретные моменты времени, интервал, между которыми Т называется тактом. При этом в каждый дискретный момент времени на вход автомата поступает одна буква входного алфавита, автомат переходит из одного состояния в другое и выдается одна буква выходного алфавита. В зависимости от того, как задается длительность такта Т, различают автоматы синхронного действия (T =const) и асинхронного действия (T 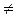const). Мы будем рассматривать, в основном, синхронные автоматы, функционирующие в дискретные моменты времени, которые можно обозначить целыми неотрицательными натуральными числами, t =0,1,2,3,…., имеющими смысл номера такта.

Для задания конечного автомата S необходимо задавать совокупность из пяти объектов: S(A, X, Y, d, l), где A = { a ₀, a ₁, a ₂,..., a _n}– множество внутренних состояний автомата, X = { x ₁, x ₂,…, x _m} – множество входных сигналов (входной алфавит), x _i – буква входного алфавита, Y = {y₁, y₂,…, y_k} – множество выходных сигналов (выходной алфавит),

d - функция переходов, определяющая состояние автомата a (t +1), в котором автомат будет находится в момент времени (t +1), в зависимости от состояния автомата a (t) и входного сигнала x (t) в момент времени t, то есть a (t +1) = d [ a (t), x (t)],

l - функция выходов, определяющая значение выходного сигнала y (t) в зависимости от состояния автомата a (t) и входного сигнала x (t) в момент времени t, т.е. y (t) = l [ a (t), x (t)].

Автомат работает следующим образом: в каждый момент времени t он находится в определенном состоянии a (t) из множества А возможных состояний. Причем в начальный момент времени t = 0 он всегда находится в состоянии a (t = 0) = a ₀. В момент времени t автомат воспринимает входной сигнал x (t), выдает выходной сигналу y (t) = l [ a (t), x (t)] и переходит в следующее состояние a (t +1)= d [ a (t), x (t)]. Другими словами абстрактный автомат каждой паре символов a (t) и x (t) ставит в однозначное соответствие пару символов a (t +1) и y (t). Такие автоматы называют детерминированными. На преобразование информации в детерминированных автоматах наложены условия.

Условия преобразования информации в детерминированных автоматах:

1. Любое входное слово, длинною l букв, преобразуется в выходное слово той же длины.

2. Если каждый раз перед подачей входных сигналов автомат находится в одном и том же состоянии, то при совпадении в двух входных словах первых l ₁ букв, в выходных словах первые l ₁ букв также совпадут.

Кроме детерминированных автоматов существуют вероятностные или стохастические автоматы, в которых переход из одного состояния в другое под воздействием случайных или детерминированных входных сигналов происходит случайно. Работа таких автоматов описывается уже матрицей переходов d, элементами которой являются вероятности переходов из одного состояния в другое. Нами будут рассмотрены, в основном, детерминированные автоматы.

Применяемые на практике автоматы принято разделять на два класса - это автоматы Мили и автоматы Мура, названные так по имени американских ученых, которые впервые начали их изучать. Функционирование автоматов строго подчиняется определённым законам (законы функционирования автоматов). Законы функционирования автоматов описываются системами уравнений:

Автомат Мили:

	a(t + 1) = d[a(t),x(t)]
	y(t) = l[a(t),x(t)]
	t = 1,2,3…

Автомат Мура:

	a(t + 1) = d[a(t),x(t)]
	y(t) = l[a(t)]
	t = 1,2,3…

Отличительной особенностью автоматов Мили является то, что их выходные сигналы зависят как от состояния автомата, так и от значения входного сигнала. В автоматах Мура выходные сигналы y (t) в каждый дискретный момент времени t однозначно определяются состоянием автомата в тот же момент времени и не зависят от значения входного сигнала.

Способы задания автоматов

Чтобы задать конечный автомат S, необходимо описать все элементы множества S = { A, X, Y, d, l }. То есть необходимо описать входной, выходной алфавиты и алфавит состояний, а также функции переходов d и выходов l. При этом среди множества A = { a ₀, a ₁,…, a _n} необходимо выделить начальное состояния a ₀, в котором автомат находится в момент времени t = 0. Существует несколько способов задания работы автомата, но наиболее часто используются табличный и графический.

Дата добавления: 2014-10-31