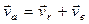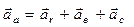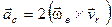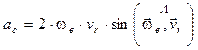Абсолютного прискорення точки

Визначення абсолютної швидкості і

Необхідні для виконання завдання К-7

Складний рух точки

Складний рух точки – це такий рух точки, який досліджується одночасно в нерухомій і рухомій системах координат.

Розглянемо рух точки М відносно системи рухомих осей координат Охуz, які в свою чергу рухаються відносно осей О₁х₁у₁z₁. Систему осей О₁х₁у₁z₁ вважатимемо нерухомою (рис.1). Рухома система координат Охуz жорстко зв’язана з тілом D по якому рухається точка М.

1. Рух точки М відносно нерухомих осей координат О₁х₁у₁z₁. називається абсолютним рухом.

Рівняння абсолютного руху точки М: .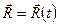

Абсолютною траєкторією точки М називають її траєкторію відносно нерухомих осей координат.

Абсолютною швидкістю 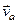і абсолютним прискоренням 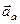точки М називають швидкість і прискорення точки відносно нерухомої системи координат.

2. Рух точки М відносно рухомої системи координат Охуz називається відносним рухом. Рівняння відносного руху точки М: ..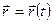

Відносною траєкторією точки М називають її траєкторію відносно рухомої системи координат.

Відносною швидкістю 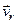і відносним прискоренням 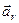точки М називають швидкість і прискорення точки відносно рухомої системи координат (від лат. relativus- відносний).

3. Переносним рухом точки М називається рух відносно нерухомої системи координат тієї точки рухомої системи координат, з якою в даний момент збігається точка, що рухається.

Переносною швидкістю 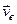і переносним прискоренням точки М називають швидкість і прискорення тієї точки рухомої системи координат, з якою в даний момент часу збігається точка, що рухається (від лат. entainer - переносити).

4. Основна задача складного руху точки полягає в тому, щоб встановити залежності між кінематичними характеристиками абсолютного, відносного і переносного рухів.

Теорема про додавання швидкостей

Теорема. Абсолютна швидкість точки при її складному русі дорівнює векторній сумі відносної і переносної швидкостей

(1)

Теорема про додавання прискорень

(теорема Коріоліса)

Теорема. Абсолютне прискорення точки при її складному русі дорівнює векторній сумі відносного, переносного та коріолісового прискорень.

(2)

Модуль і напрям коріолісового прискорення

Коріолісове прискорення визначається за формулою

(3)

де 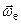– вектор кутової швидкості переносного руху;

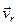– вектор відносної швидкості точки.

Коріолісове прискорення є результатом взаємного впливу двох рухів – переносного і відносного.

Модуль коріолісового прискорення визначається за формулою:

(4)

Напрям коріолісового прискорення знаходять за правилом визначення напряму векторного добутку (3).

Коріолісове прискорення може дорівнювати нулю в трьох випадках:

1) якщо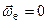, тобто при поступальному переносному русі;

2) якщо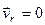, тобто відсутній відносний рух;

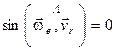
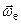3) якщо, тобто якщо вектори і 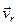паралельні.

Визначення відносної швидкості і відносного прискорення точки М

1. Якщо відносний рух точки заданий координатним способом, то:

, .

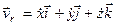2. Якщо відносний рух точки заданий природним способом, то:

, , , .

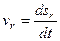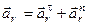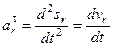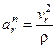Визначення переносної швидкості і переносного прискорення точки М

1. Якщо переносний рух поступальний (дивись рис.1), то:

, .

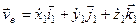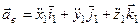2. Якщо переносний рух обертальний, то:

, , , .

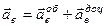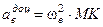де МК – найкоротша відстань від точки М до осі обертання.

Модуль і напрям абсолютного прискорення точки М

Для визначення абсолютного прискорення застосовують метод проекцій. Для цього необхідно побудувати прямокутну систему осей з початком в точці М і проектуючи рівність (2) на кожну з цих осей, знаходимо:

, , .

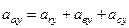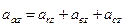Модуль абсолютного прискорення точки М знаходимо за формулою:

.

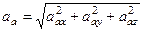Напрям вектора абсолютного прискорення точки М знаходимо за напрямними косинусами:

, , .

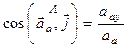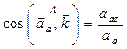Дата добавления: 2014-10-31