Г. Стаханов 2 страница

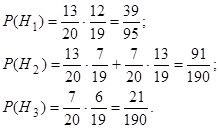
Вычислим условную вероятность 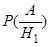. Если предположить, что событию Н₁, наступило, т.е. из первой урны по вторую переложены два белых шара, то во второй урне окажется шесть белых и шесть чёрных шаров. Поэтому 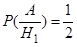. Аналогично вычислим 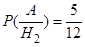; 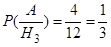. Вероятность события А найдем по (3.1):

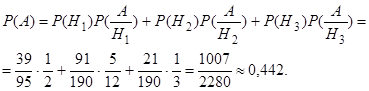
Пример 3.2. На сборку поступают детали о двух автоматов. Производительность первого автомата в 3 раза больше производительности второго. Первый автомат допускает 1% брака деталей, второй - 0,5%. На сборку поступила бракованная деталь. Найти вероятность того, что эта деталь изготовлена первым автоматом.

Решение. Обозначим через А событие "на сборку поступила бракованная деталь". Можно выдвинуть две гипотезы: Н₁ - деталь произведена первым автоматом; Н₂ - деталь произведена вторим автоматом.

В задаче требуется найти условную вероятность Р(). Поскольку первый автомат производит в 3 раза больше деталей, чем второй, то Р(Н₁)=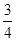, Р(Н₂)=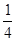. Условная вероятность Р(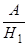) (вероятность того, что деталь будет бракованной, если она произведена первым автоматом), равна 0,01; Р(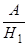)= 0.01; аналогично Р()= 0,005. Искомую условную вероятность Р() найдем по формуле Бейеса (3.2):

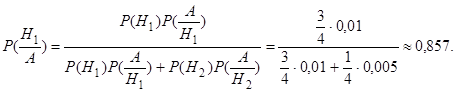
Варианты задачи 3.

3.1. На заводе, изготовляющем болты, первый станок производит 25%, второй – 35%, третий – 40%; всех изделий. В их продукции брак составляет соответственно 3%, 2% и 1%. Найти вероятность того, что случайно выбранный болт имеет дефект.

3.2. Имеются две урны: в первой семь белых и три черных, а во второй - пять белых и пять черных шаров. Из второй урны наудачу переложили в первую два шара. После этого из первой урны вынули один шар. Найти вероятность того, что вынутый шар окажется белым.

3.3. В батарее 20 орудий, из них два нестандартных. Вероятность попадания в цель из пристрелянного орудия равна 0,8, из не пристрелянного - 0,3. Найти вероятность поражения цели, если будет произведен один выстрел из наудачу выбранного орудия.

3.4. В цехе работает 20 станков. Из них 10 станков марки А, 4 - марки В и 6 - марки С. Вероятность того, что качество деталей окажется отличным, для этих станков равна соответственно 0,9; 0,7; 0,8. Какой процент деталей отличного качества выпускает цех?

3.5. Радиолампа может принадлежать однойиз четырёх партий с вероятностями р₁=0,3; р₂=0,2; р₃=0,4; р₄= 0,1. Вероятность того, что лампа проработает заданное время, для этих партий равна соответственно 0,4; 0,6; 0,8; 0,7. Найти вероятность того, что наудачу выбранная лампа проработает это заданное время.

3.6. В каждой из двух урн находится по 12 белых и восемь черных шаров. Из первой урины наудачу переложили во вторую два шара, а затем из второй урны вынули наугад один шар. Найти вероятность того, что вынутый шар окажется черним.

3.7. В продажу поступают телевизоры трёх заводов. Продукция первого завода содержит 10% телевизоров со скрытым дефектом, второго - 7%,третьего – 5%. Найти вероятность приобретения исправного телевизора, если магазин получил 30% телевизоров с первого завода, 25% - со второго и 15% - с третьего.

3.8. В каждом из трех ящиков находятся детали: в первом 18 стандартных и две бракованные, во втором - девять стандартных и одна бракованная, а третьем - 12 стандартных и три бракованные. Из наудачу выбранного ящика извлекли деталь. Найти вероятность того, что она окажется стандартной.

3.9. На сборку поступают шестерни с трех автоматов. Первый автомат даёт 20%, второй – 30%, третий – 50% шестерён. Первый автомат допускает 0,2% брака, второй - 0,3%, третий – 0,4%. Найти вероятность поступления на сборку бракованной шестерни.

3.10. В первой урне находится семь белых и три черных, во второй - шесть белых и четыре чёрных, в третьей - девять белых и шесть чёрных шаров. Найти вероятность того, что наугад вынутый шар из наудачу выбранной урны окажется белым.

3.11. С первого автомата на сборку поступает 30%, со второго –25%, с третьего – 20%, с четвёртого – 25% деталей. Среди деталей первого автомата 0,2% бракованных, второго - 0,1%, третьего - 0,25%, четвертого - 0,3%. Найти вероятность того, что поступившая на сборку деталь окажется бракованной.

3.12. При передачесообщения сигналена "точка" и "тире" они встречаются в отношении 5:3. Статистические свойства помех таковы, что искажается в среднем 2/5 сообщений "точка" и1/3 сообщений "тире". Найти вероятность того, что произвольный из принятых сигналов не искажён.

3.13. Стреляют по 10 мишеням типа А, по шести - типа В и по четырём - типа С. Вероятность попадания при одном выстреле в мишень типа А ровна 0,6, типа В - 0,5, типа С - 0,4. Найти вероятность поражения мишени при одном выстреле, если не известно, в мишень какого типа он будет произведен.

3.14. Для контроля продукции из одной из трех партий деталей наудачу взята для испытания одна деталь. Найти вероятность того, что она окажется бракованной, если в первой партии 2/3 деталей бракованные, во второй - 1/3. а в третьей все детали хорошего качества.

3.15. Прибор, установленный на борту самолета, может работать в двух режимах: в условиях нормального крейсерского полёта и перегрузки при взлете и посадке. Первый режим осуществляется в 80% всего времени полёта, второй - в 20%. Вероятность выхода прибора из строя за время полёта в нормальном режиме равна 0,15, в условиях перегрузки - 0,45. Найти вероятность безотказной работы прибора за время полёта.

3.16. Детали изготовляют на двух заводах. Объём продукции второго завода в 2 раза больше, чем первого. Среди деталей первого завода 3% бракованных, второго – 2%. Найти вероятность того, что наудачу взятая деталь окажется не бракованной.

3.17. В двух ящиках находится по 20 деталей: причём в первом 15 из них стандартных, во второй - 18. Из первого ящика наудачу извлечена одна деталь, и переложена во второй. Найти вероятность того, что наудачу извлеченная после этого деталь из второго ящика будет стандартной.

3.18. Наборщик пользуется двумя кассами: в первой 85%, во второй – 95% шрифта отличного качества. Найти вероятность того, что наугад извлеченная литера из наудачу взятой кассы будет отличного качества.

3.19. В партии 600 лампочек: из них-200 изготовлены на первом, 300 - на втором, 100 - на третьем заводе. Вероятность того, что лампочка окажется нестандартной, для первого завода равна 0,07, для второго - 0,1, для третьего - 0,05. Найти вероятность того,что наудачу взятая из партии лампочка окажется стандартной.

3.20. В первой урне содержится 12 белых и восемьчёрных, во второй - четыре белых и шесть чёрных шаров. Из первой урны наудачу переложили во вторую два шара. Найти вероятность того, что шар, вынутый после этого из второй урны, окажется чёрным.

3.21. В урну, в которой находится три шара, опушен один белый шар, после чего из неё наудачу извлечён также один шар. Найти вероятность того, что извлечённый шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров в урне (поцвету).

3.22. В ящике находится 20 деталей, изготовленных на первомзаводе, 16 -на втором, 14 - на третьем. Среди деталей, изготовленных на первом заводе, 90% отличного качества, на втором – 80%, на третьем – 95%. Найти вероятность того, что извлеченная наудачу деталь окажется отличного качества.

3.23. Имеется две партииизделий по 20 и 30 шт., причём вкаждой из них есть по два бракованных изделия. Изделие, взятое наудачу из первой партии, переложено во вторую, после чего наудачу выбрано изделие из второй партии. Найти вероятность того, что это изделие окажется бракованным.

3.24. Три перфораторщицы набили по одинаковому комплекту перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,1; для второй и третьей перфораторщиц эти вероятности равны соответственно 0,15 и 0,12. Найти вероятность того, что наудачу выбранная перфокарта содержит ошибку.

3.25. Имеется три одинаковые урны: первая содержит четыре белых и восемь чёрных, вторая - 18 белых и шесть чёрных, третья - семь белых и пять чёрных шаров. Найти вероятность того, что наугад извлеченный шар из наудачу выбранной урны окажется чёрним.

3.26. В ящике находится 10 теннисных мячей, восемь из которых новые. Для первой игры наугад берут два мяча, которые после игры возвращают в ящик. Для второй игры также наугад берут два мяча. Найти вероятность того, что мячи, взятые для второй игры, новые.

3.27. В первой урне находятся 14 белых и 11 чёрных, во второй -10 белых и 15 чёрных шаров. Из второй урны наудачу переложили в первую один шар, после чего из первой урны вынули наугад один шар. Найти вероятность того, что этот шар окажется белим.

3.28. В тире имеется пять ружей, вероятность попадания в мишень из которых при одном выстреле равна соответственно 0,6; 0,7; 0,8; 0,9; 0,5. Определить вероятность попадания в мишень при одном выстреле, если стрелок берёт одно из ружей наудачу.

3.29. Имеется две партии изделий по 10 и 15 шт., причем в каждой из них есть по два бракованных изделия. Два изделия, взятые наудачу из первой партии, переложены во вторую, после чего выбрано наудачу одно изделие из второй партии. Найти вероятность того, что это изделие окажется бракованным.

3.30. На сборку поступают детали из двух автоматов. Первый даёт 1% брака, второй - 0,5%. Найти вероятность того, что на сборку поступит бракованная деталь, если всего на сборку с первого автомата поступает 3000, со второго - 2000 деталей.

Варианты задачи 4.

4.1. Два стрелка независимо друг от друга стреляют по одной мишени, причём каждый из них делает по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,5, для второго – 0,7. После стрельбы обнаружена одна пробоина в мишени. Найти вероятность того, что она принадлежит второму стрелку.

4.2. В партии 800 лампочек: 300 изготовлены на первом заводе, 400 - на втором, 100 - на третьем. Вероятность того, что лампочка окажется стандартной, для первого завода равна 0,95, для второго -0,9, для третьего - 0,92. Наудачу взятая из партии лампочка оказалась не стандартной. Найти вероятность того, что она изготовлена на первом заводе.

4.3. На заводе, изготовляющем болты, первый станок производит 30%, второй – 45%, третий – 25% всех изделий. В их продукции браксоставляет соответственно 4, 3, 2%. Случайно выбранный из продукции болт оказался бракованным. Найти вероятность того, что он изготовлен на втором станке.

4.4. В первой урне содержится три белых и семь чёрных, во второй - пять белых и пять чёрных шаров. Из первой урны наудачу переложили во вторую два шара. После этого из второй урны вынули один шар. Он оказался белим. Найти вероятность того, что из первой урны во вторую переложили два белых шара.

4.5. На трёх станках изготовляют детали одного наименования: на первом – 20%, на втором – 35%, на третьем – 45% всех деталей. Вероятность каждой детали быть бездефектной равна 0,8, если она изготовлена на первом станке, 0,9 - если на втором, 0,7 - если на третьем. Наудачу взятая деталь оказалась бездефектной. Найти вероятность того, что она изготовлена на третьем станке.

4.6. Однотипные приборы выпускаются тремя заводами в количественном отношении 2:3:5, причём вероятность брака для этих заводов равна соответственно 0,03; 0,1; 0,05. Прибор, приобретённый лабораторией, оказался бракованным. Найти вероятность того, что данный прибор выпущен третьим заводом.

4.7. Две перфораторщицы набили по одинаковому комплекту перфокарт. Вероятность того, что первая перфораторщица допустила ошибку, равна 0,15. вторая - 0,1. При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошибку допустила первая перфораторщица.

4.8. В урне лежит шар неизвестного цвета - с равной вероятностью белый или чёрный. В урну опустили один белый шар, и после тщательного перемешивания наудачу извлекли также один вир. Он оказался белым. Найти вероятность того, что в урне остался белый шар.

4.9. Из первого ящика, в котором находится 17 стандартных и три бракованные детали, переложили наугад одну деталь во второй ящик, в котором находится восемь стандартных и две бракованные детали. Затем из второго ящика наудачу извлекли деталь. Она оказалась стандартной. Найти вероятность того, что из первого ящика во второй переложили бракованную деталь.

4.10. На сборку поступают детали из двух автоматов. Первый даёт 98% качественных деталей, второй – 99%. На сборку поступила бракованная деталь. Найти вероятность того, что она изготовлена на первом автомате, если всего на сборку с первого автомата поступает 2000, со второго - 1000 деталей.

4.11. В ящике находится восемь теннисных мячей, пятьиз которых новые. Для первой игры наугад взяли два мяча, которые после игры возвратили в ящик. Для второй игры взяли наугад также два мяча, которые оказались новыми. Найти вероятность того, что мячи, взятые для первой игры, также были новыми.

4.12. Среди поступавшихна сборку деталей с первого автомата 0,15% бракованных, со второго - 0,2%, с третьего - 0,25%, с четвёртого - 0,4%. Производительности автоматов относятся соответственно, как 4:3:2:1. Взятая наудачу деталь оказалась стандартной. Найти вероятность того, что она изготовлена на втором автомате.

4.13. Среди 300 изделий 150 первого сорта, 100 - второго, 50 -третьего. Вероятность брака среди изделий первого сорта 0,01, второго - 0,02, третьего - 0,05. Взятое наудачу изделие оказалось не бракованным. Найти вероятность того, что это изделие первого сорта.

4.14. С первого автомата на сборку поступает 60%, со второго –40% всех деталей. На первом автомате брак составляет 2%, на втором – 3%. На сборку поступила бракованная деталь. Найти вероятность того, что она изготовлена на первом автомате.

4.15. Имеется три одинаковых по виду ящика. В первом ящике 15 белых и пять черных, во втором - 20 черных, в третьем - 13 белых и семь чёрных шаров. Из выбранного наугад ящика вынули шар. Он оказался белым. Найти вероятность того, что шар вынут из третьего ящика.

4.16. Наборщик пользуется двумя кассами. В первой кассе – 80%, во второй; - 93% шрифта отличного качества. Наугад извлеченная литера из наудачу взятой кассы оказались отличного качества. Найти вероятность того, что она вынута из второй кассы.

4.17. В пирамиде установлено 20 винтовок, шесть из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95, без оптического прицела - 0,75. Стрелок поразил мишень из наудачу взятой винтовки. Найти вероятность того, что он стрелял из винтовки без оптического прицела.

4.18. Имеется три партии деталей по 30 в каждой. Число стандартных деталей в первой, второй и третьей партии равно соответственно 28, 25 и 20. Из наудачу взятой партии извлечена деталь, оказавшаяся стандартной. Найти вероятность того, что эта деталь извлечена из второй партии.

4.19. Имеется три одинаковых урны: в первой находится три белых и семь чёрных, во второй - 15 белых и пять чёрных, в третьей - восемь белых и семь чёрных шаров. Из наудачу выбранной урны вынут шар. Он оказался чёрным. Найти вероятность того, что шар вынут из третьей урны.

4.20. На сборку поступают детали с трех автоматов. Первый автомат даёт 0,5% брака, второй - 1%, третий - 0,75%. На сборку поступила бракованная деталь. Найти вероятность того, что она изготовлена на втором автомате, если всего на сборку с первого автомата поступает 2000, со второго - 3000, с третьего - 5000 деталей.

4.21. В батарее 15 орудий, два из них не пристрелянных. Вероятность попадания в нуль из пристрелянного орудия равна 0,75, из пристрелянного - 0,24. Сделали один выстрел, и не попали в цель. Найти вероятность того, что выстрел произведениз не пристрелянного орудия.

4.22. Три стрелка произвели выстрел, причём две пули поразили мишень. Найти вероятность того, что поразил мишень первый стрелок, если вероятность попадания в мишень первым, вторым и третьим стрелками равна соответственно 0,8; 0,7; 0,6.

4.23. В специализированную больницу в среднем поступает 40% больных с заболеванием К, 35% - с заболеванием М и 25% - с заболеванием N. Вероятность полного излечения болезни К равна 0,8, болезни М- 0,7, болезни N - 0,05. Больной, поступивший в больницу, был выписан здоровым. Найти вероятностьтоги, что он страдалзаболеванием N.

4.24. Имеется 10 одинаковых урн, в семииз которых находится по три чёрных и пять белых, а в трёх - по шесть чёрных и четыре белыхшара. Из урны, взятой наудачу, извлечен шар. Он оказался белым. Найти вероятность того, что шар извлечён из урны, в которой находится шесть чёрных и четыре белых шара.

4.25. Радиолампа может принадлежать к одной из трёх партий с вероятностями р, = 0.4; Р = 0,5; /',= 0,1. Вероятность того, что лампа проработает заданное число часов, для этих партий равна соответственно 0,3; 0,4; 0,8. Лампа проработала заданное число часов. Найти вероятность того, что она принадлежит к первой партии.

4.26. Имеется два одинаковых по виду ящика. В первом ящике 15 стандартных и пять стандартных, по втором - семь стандартных и три нестандартные детали. Из выбранного наудачу ящика вынули одну деталь. Она оказалась стандартной. Найти вероятностьтого, что эту деталь вынули из второго ящика.

4.27. Известно, что 95 % выпускаемой продукции соответствует стандарту. Упрощенная схема контроля признает пригодной стандартную продукцию с вероятностью 0,97 и нестандартную - с вероятностью 0,06. Найти вероятность того, что изделие, прошедшее упрощенный контроль, удовлетворяет стандарту.

4.28. Партия холодильников выпущена московским и минским заводами. Из них 60% холодильников выпущено минским заводом. Для холодильников московского завода вероятность безотказной работы в течение времени t равна 0,95, минского - 0,92. Случайно выбранный холодильник работал безотказно течении времени t. Найти вероятность того, что это холодильник московского завода.

4.29. В урну, в которой находится дна шара, опущен один белый шар, после чего из неё начудачу извлечён один шар. Он оказался белым. Найти вероятность того, что первоначально в урне находились один белый и один небелый шары (все предположения о первоначальном составе шаров в урне равновозможные).

4.30. Прибор состоит из двух узлов. Работа каждого узла необходима для работы прибора в целом. Вероятность работы первого узла 0,8, второго - 0,9. Прибор вышел из строя. Найти вероятность того, что отказал только первый узел.

4. ПОВТОРЕНИЕ ИСПЫТАНИЙ. ФОРМУЛА БЕРНУЛЛИ. НАИВЕРОЯТНЕЙШЕЕ ЧИСЛО ПОЯВЛЕНИЯ СОБЫТИЯ В НЕЗАВИСИМЫХ ИСПЫТАНИЯХ.

Несколько испытаний называются независимыми, если вероятность того или иного исхода каждого из испытании не зависит от того, какие исходы имели другие испытания.

Если в каждой из n независимых испытаний вероятность появления события А постоянна и равна р, то вероятность того, что в этих n испытаниях событие А наступитm раз, выражается формулой Бернулли: 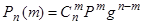, (4.1.)

где 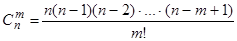; g=1-p.

Число m, появлений события А в n независимых испытаниях, в каждой из которых вероятность появления события равна p, называется наивероятнейшим, если вероятность того, что событие А наступит в этих испытаниях m₀ раз, не меньше вероятностей остальных возможных исходов испытаний. Число m₀ определяется из двойного неравенства

np-g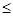m₀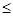np+p. (4.2.)

Следует отметить, что разность чисел np-g и np+p равна единице. Если np+p не является целым числом, то существует одно наивероятнейшее число m₀. В частности, если np - целое число, то m₀=np.Если np+p - целое число, то существует два наивероятнейших числа m₀^'=npg, m₀^"=np-p.

Пример 4.1. Вероятность выиграть по одному билету лотереи 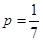. Найти вероятность выигрыша при наличии шести билетов: а) по двум билетам; б) не более чем по двум билетам; в) не менее чем по двум билетам; г) хотя бы по одному билету.

Решение: а) по условию n=6, m= 2, 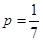, 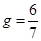. Воспользуемся формулой Бернулли (4.1.):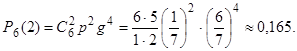

б) обозначим искомую вероятность 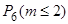. Выиграть не более чем по двум билетам из шести означает, что среди шести билетов будет или один выигрышный, или два выигрышных, или не будет ни одного выигрышного, т.е.

;

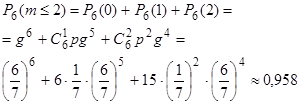в) вероятность того, что из шести билетов будет не менее чем два выигрышных:

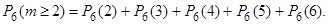
В данном случае проще найти вероятность противоположного события. Среди шести билетов нет ни одного выигрышного, или есть один выигрышный и вычесть её из единицы:

;

г) выиграть хотя бы по одному билету из шести означает, среди этих шести билетов будет не менее одного выигрышного. В данном случае также проще найти вероятность противоположного события (среди шести билетов нет ни одного выигрышного) и вычесть из единицы:

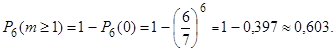
Пример 4.1. ОТК проверяет партию из 10 деталей. Вероятность того, что деталь стандартная, равна 0,85. Найти наивероятнейшее число стандартных деталей в этой партии.

Решение. По условию p=0,85, n=10, g=1-p=0,15. Число m₀ определяется из двойного неравенства (2), т.е.

10ּ0,85-0,15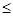m₀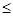10ּ0,85+0,85, или 8,35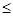m₀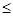9,35. Поскольку m₀ – целое число то, очевидно, что m₀=9.

Варианты задачи 5.

Вероятность появления события А в каждом из n независимых испытаний постоянна и равна p. Найти:

1) вероятность того, что в n независимых испытаниях событие А появится: а) m раз; б) не менее m раз; в) не более m раз; г) хотя бы 1 раз;

2) наивероятнейшее число появления события А в независимых испытаниях и вероятность наивероятнейшего числа появлений события А в этих испытаниях:

5.1.	n=5	m=2	p=0,6
5.2.	n=8	m=7	p=0,7
5.3.	n=6	m=4	p=0,5
5.4.	n=8	m=3	p=0,6
5.5.	n=5	m=4	p=0,9
5.6.	n=6	m=5	p=0,4
5.7.	n=7	m=3	p=0,6
5.8.	n=7	m=5	p=0,8
5.9.	n=5	m=2	p=0,3
5.10.	n=6	m=2	p=0,7
5.11.	n=5	m=3	p=0,2
5.12.	n=4	m=3	p=0,5
5.13.	n=7	m=3	p=0,9
5.14.	n=6	m=3	p=0,6
5.15.	n=4	m=2	p=0,2
5.16.	n=6	m=2	p=0,4
5.17.	n=6	m=3	p=0,3
5.18.	n=7	m=4	p=0,7
5.19.	n=5	m=3	p=0,9
5.20.	n=6	m=4	p=0,5
5.21.	n=7	m=5	p=0,8
5.22.	n=4	m=2	p=0,6
5.23.	n=5	m=3	p=0,7
5.24.	n=6	m=5	p=0,4
5.25.	n=5	m=4	p=0,6
5.26.	n=6	m=3	p=0,2
5.27.	n=7	m=5	p=0,3
5.28.	n=4	m=2	p=0,9
5.29.	n=5	m=3	p=0,8
5.30.	n=6	m=4	p=0,7

5. ЛОКАЛЬНАЯ И ИНТЕГРАЛЬНАЯ ТЕОРЕМЫ МУАВРА-ЛАПЛАСА. ФОРМУЛА ПУАССОНА.

Если число испытаний n велико, применение формулы Бернулли приводит к громоздким вычислениям. Поэтому в таких случаях используют асимптотические формулы.

Локальная теорема Муавра-Лапласа. Если вероятность p появления события А в каждом из n независимых испытаний постоянна, причём 0<p<1, а число испытаний достаточно велико, то вероятность того, что в этих испытаниях событие А наступит m раз,

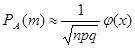, где ; .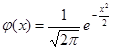

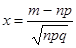Функция чётная: 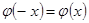. Имеются таблицы, в которых приведены значения функции , соответствующие положительным значениям аргумента; для x>5 полагают .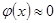

Формула Пуассона. Если в каждом из n независимых испытаний вероятность p появления события А постоянна и мала (p<0,1), а число испытаний n достаточно велико, то вероятность того, что событие А наступит в этих испытаниях m раз, 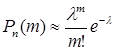, где 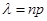. (5.1.)

Для функции 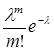, которая является функцией двух переменных и m, имеются таблицы.

Интегральная теорема Муавра-Лапласа. Если вероятность p события А в каждом изnнезависимых испытаний постоянна, причём 0<p<1, а число испытаний достаточно велико, то вероятность того, что в этих испытаниях событие А наступит не менее m₁ раз и не более m₂ раз, 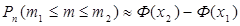, где Ф(х)- функция Лапласа,

.

Функция Лапласа нечётная: Ф(х)= - Ф(х). Имеются таблицы значений этой функции для положительных значений х: для x>5 полагают Ф(х)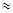0,5.

Вероятность отклонения относительной частоты события от его вероятности в независимых испытаниях. Если вероятность p появления события А в каждом из n независимых испытаний постоянна (0<p<1), а число испытаний достаточно велико, то вероятность того, что отклонение относительной частоты 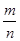события А от его вероятности p по абсолютной величине не превзойдёт заданного числа 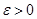, 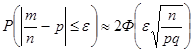. (5.2.)

Дата добавления: 2014-10-31