Г. Стаханов 5 страница

13.1.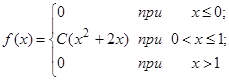
13.2.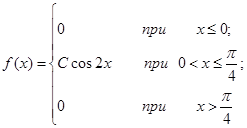
13.3.
13.4.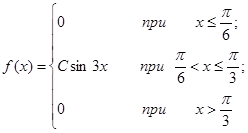
13.5.
13.6.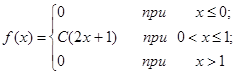
13.7.
13.8.
13.9.
13.10.
13.11.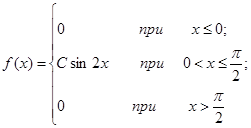
13.12.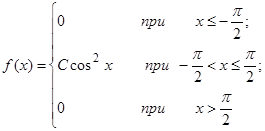
13.13.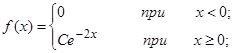
13.14.
13.15.
13.16.
13.17.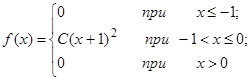
13.18.
13.19.
13.20.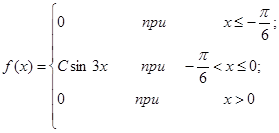
13.21.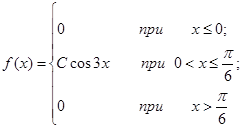
13.22.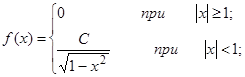
13.23.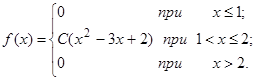
13.24.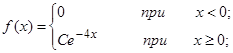
13.25.
13.26.
13.27.
13.28.
13.29.
13.30.

8. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ. ПОНЯТИЕ О ЦЕНТРАЛЬНОЙ ПРЕДЕЛЬНОЙ ТЕОРЕМЕ ЛЯПУНОВА

Распределение вероятностей непрерывной случайной величины Х называется нормальным, если плотность распределения вероятностей 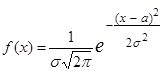, где a –математическое ожидание; - среднеквадратическое отклонение случайной величины Х.

Вероятность того, что нормально распределённая случайная величина Х примет значение, принадлежащее интервалу ,

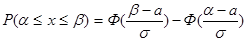, (8.1.)

где Ф(х) – функция Лапласа, .

Вероятность того, что отклонение нормального распределения случайной величины Х от её математического ожидания а не превзойдёт по абсолютной величине заданного числа ,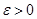

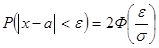(8.2.)

Нормальный закон – это наиболее часто встречающийся на практике закон распределения, которому подчинены многие случайные величины, например погрешности измерений, отклонения размеров изготовляемых деталей от номинального, ошибки стрельбы. Чем это объясняется? Ответ на этот вопрос был дан выдающимся русским математиком А. М. Ляпуновым. Содержание центральной предельной теоремы Ляпунова: если случайная величина Х представляет собой сумму очень большого числа независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

Приведём формулировку центральной предельной теоремы для одинаково распределённых слагаемых: если Х₁, Х₂, …,Х_n – независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием a и дисперсией 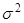, то при неограниченном увеличении n закон распределения суммы неограниченно приближается к нормальному.

Рассмотрим среднее арифметическое этих случайных величин .

При достаточно большом n 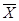также имеет распределение, близкое к нормальному.

Поскольку М(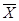)= а; D(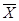)=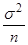, вероятность того, что 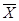попадёт в интервал : .

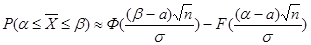Вероятность того, что отклонение среднего арифметического 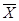от математическое ожидания а не превзойдёт по абсолютной величине заданного числа ,

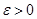(8.3.)

Пример 8.1. Математическое ожидание и среднеквадратичное отклонение нормально распределённой случайной величины Х равны соответственно 10 и 4. Найти вероятность того, что в результате испытания Х примет значение, находящееся в интервале (8, 15).

Решение. Воспользуемся формулой (8.1.). Подставив значение 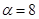, , 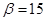а =10, , получим . По таблице значений функции Лапласа найдём Ф(1,25)=0,3944; Ф(0,5)=0,1915. Искомая вероятность .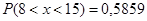

Пример 8.2. Измеряют диаметр вала без систематических погрешностей. Случайные погрешности измерения Х подчинены нормальному закону с математическим ожиданием а =0 и среднеквадратическим отклонением .

Решение. Прежде всего найдём вероятность того, что одно измерение будет произведено с погрешностью, не превосходящей по абсолютной величине 10 мм. Используем формулу (8.2). Принимая а=0, =20, =10, находим .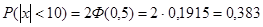

Следовательно, р=0,383.

Вероятность того, что одно измерение будет произведение с погрешностью; превосходящей по абсолютной величине 10 мм, q=1-p=0,617.

Пусть событие А состоит в том, что погрешность хотя бы одного из трёх независимых измерений не превзойдёт по абсолютной величине 10 мм. Тогда Р(А)=1-Р(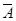), где 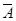- противоположное событие, состоящее в том, что погрешности всех трёх измерений превзойдут по абсолютной величине 10 мм.

Значение Р(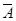) вычислим по формуле Бернулли (4.1.): Р(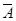)=q³=0,617³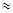0,235.

Искомая вероятность Р(А)=1-0,235=0,765.

Пример 8.3. Пусть Х₁, Х₂, …,Х_n – независимые одинаково распределённые случайные величины с математическим ожиданием a и дисперсией 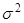=3; 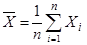- среднее арифметическое. Найти такое положительное 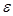, чтобы с вероятностью =0,95 можно было ожидать, что среднее арифметическое 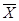отклониться от математического ожидания а по абсолютной величине не более чем на , если n=2700.

Решение. Используем формулу (8.3.): .

Обозначим 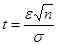, тогда . По таблице значений функции Лапласа найдём Ф(1,96)=0,475.

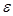Следовательно, t=1,96, т.е. . Для нахождения получим уравнение .

Задача 14. Найти вероятность попадания в заданный интервал нормально распределённой случайной величины Х, если известны её математическое ожидание а и среднеквадратичное отклонение .

14.1.	= -3	=6	=1	=3
14.2.	=2	=6,5	=5	=2
14.3.	=5	=8	=3	=4
14.4.	=0	=5,4	=2	=2
14.5.	=1	=10	=4	=5
14.6.	=4	=11	=7	=3
14.7.	=3	=12	=6	=4
14.8.	=4	=15	=8	=6
14.9.	=13	=18	=16	=5
14.10.	=16	=20	=15	=3
14.11.	=3,3	=5,7	=4	=1
14.12.	=7	=14	=9	=6
14.13.	=12	=23	=18	=4
14.14.	=15	=25	=19	=5
14.15.	=15	=18	=17	=1
14.16.	=13	=21	=16	=2
14.17.	=15	=20	=14	=3
14.18.	=12	=18	=13	=4
14.19.	=3,5	=12	=6	=5
14.20.	=6	=10	=5	=2
14.21.	=4	=10	=8	=3
14.22.	=13	=17	=12	=4
14.23.	=11	=22	=13	=5
14.24.	=14	=24	=15	=4
14.25.	=14	=22	=17	=2
14.26.	=8	=13	=6	=3
14.27.	= -2	=8	=2	=5
14.28.	=6,5	=9,8	=8	=1
14.29.	=4	=15	=9	=4
14.30.	=10	=16	=12	=3

Задача 15. Измеряют некоторую физическую величину без систематических погрешностей. Случайные погрешности измерения Х подчинены нормальному закону с математическим ожиданием a =0 и среднеквадратичным отклонением . Найти вероятность того, что: а) одно измерение будет произведено с погрешностью, не превосходящей по абсолютной величине заданного положительного числа ; б) изn независимых измерений погрешность хотя бы одного не превзойдёт по абсолютной величине числа .

15.1.	=2	=1	3	15.2.	=4	=5	2
15.3.	=10	=4	3	15.4.	=9	=3	4
15.5.	=5	=4	2	15.6.	=10	=6	4
15.7.	=3	=1,5	3	15.8.	=20	=15	4
15.9.	=8	=5	3	15.10.	=8	=2	5
15.11.	=4	=6,4	2	15.12.	=2,5	=3	3
15.13.	=10	=7,5	2	15.14.	=6	=4	3
15.15.	=3	=2,4	3	15.16.	=2	=3	2
15.17.	=4	=3	3	15.18.	=5	=2	3
15.19.	=7	=4,2	4	15.20.	=8	=6	2
15.21.	=1	=0,8	3	15.22.	=0,9	=1	3
15.23.	=4	=2	4	15.24.	=5	=3	2
15.25.	=2	=2	3	15.26.	=3	=2	3
15.27.	=2	=1,5	3	15.28.	=3	=1	4
15.29.	=8	=4	3	15.30.	=2	=2,5	2

Задача 16. Х₁, Х₂, …,Х_n – независимые одинаково распределённые случайные величины с математическим ожиданием a и дисперсией 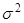; 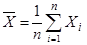- среднее арифметическое.

Дата добавления: 2014-10-31