Г. Стаханов 4 страница

7.1. Случайная величина и закон её распределения.

Случайной называется величина, которая в результате испытания примет одно и только одно возможное значение, заранее неизвестное и зависящее от случайных причин.

Случайная величина называется дискретной, если она может принимать лишь конечное или счётное число испытаний.

Непрерывной называется случайная величина, возможные значения которой заполняют некоторый промежуток (конечный или бесконечный).

Законом распределения случайной величины называется соотношение, устанавливающее связь между её возможными значениями и соответствующими им вероятностями.

Закон распределения дискретной случайной величины может быть задан в виде таблицы, в которой приводят возможные значения случайной величины и соответствующие им вероятности.

xi	x1	x2	…	xn
pi	p1	p2	…	pn

Такая таблица называется рядом распределения дискретной случайной величины Х.

Закон распределения дискретной случайной величины Х можно изобразить графически, для чего в прямоугольной системе координат строят точки М₁(х₁;р₁), М₂(х₂;р₂),…,М_n(х_n;р_n) и последовательно соединяют их отрезками прямых (полученная фигура называется многоугольником распределения), а также задать аналитически (в виде формулы): Р(х=х_i)=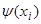. Например, пусть дискретная величина Х- это число появлений события А в n независимых испытаниях, в каждом из которых вероятность появления события А постоянна и равна р. Возможные значения Х: х₁=0, х₂=1,…, х_n+1=n. Для нахождения вероятностей этих возможных значений воспользуемся формулой Бернулли: 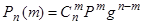, (7.1.)

Где m=0,1,2,…,n; q=1-p.

Формула (7.1.) – аналитическое выражение закона распределения вероятностей этой случайной величины Х.

Закон распределения вероятностей, определяемый формулой Бернулли, называется биноминальным.

Как дискретную, так и непрерывную случайную величину можно задать функцией распределения F(x), определяющей для каждого Х вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т.е. F(x)=P(X<x).

Функция распределения любой случайной величины является неубывающей функцией аргумента х, причём .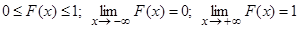

Вероятность того, что случайная величина Х примет значение, удовлетворяющее двойному неравенству .

Можно дать более точное определение непрерывной случайной величины: случайная величина Х называется непрерывной, если её функция распределения F(x) непрерывна всюду, а производная функции распределения непрерывна во всех точках, за исключением, может быть, конечного числа точек на любом конечном интервале.

Вероятность того, что непрерывная случайная величина Х примет одно определённое значение, равна нулю, т.е. Р(х=х₀)=0. Поэтому для непрерывной случайной величины Х .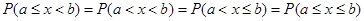

Плотностью распределения вероятностей непрерывной случайной величины Х называется первая производная от её функции распределения .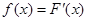

Плотность распределения вероятностей неотрицательна, т.е. .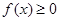

Вероятность того, что непрерывная случайная величина Х примет какое-нибудь значение из интервала (а, в): .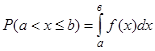

Несобственный интеграл , поскольку он выражает вероятность того, что случайная величина Х примет какое-либо значение из интервала .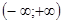

Если задана плотность распределения непрерывной случайной величины Х, то её функция распределения 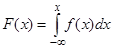. (7.2.)

Следует отметить, что плотность распределения вероятностей существует только для непрерывной случайной величины.

7.2.Числовые характеристики случайных величин.

Математическим ожиданием дискретной случайной величины Х называется сумма произведений всех её возможных значений на соответствующие им вероятности:

М(х)=х₁р₁+ х₂р₂+…+ х_nр_n.

Если дискретная случайная величина Х может принимать счётное число значений, то 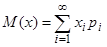при условии, что этот ряд абсолютно сходится и .

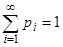Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством , где f(x) – плотность распределения вероятностей.

Предположим, что интеграл сходится абсолютно. В частности, если все возможные значения случайной величины Х принадлежат интервалу (а; в), то 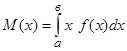. (7.3.)

Дисперсией случайной величины Х называется математическое ожидание квадрата отклонения случайной величины Х от её математического ожидания D(х)=М[X-M(x)]².

Для дисперсии случайной величины Х эта формула принимает вид 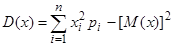. (7.4.)

Для непрерывной случайной величины Х, все возможные значения которой принадлежит интервалу (а, в), получим 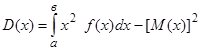. (7.5.)

Среднеквадратичным отклонением случайной величины Х называется квадратный корень из её дисперсии: .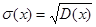

Пример 7.1. Дискретная величина Х задана законом распределения:

xi
pi	0,2	0,3	0,4	0,1

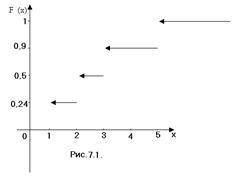
1.Найти функцию распределения F(x) и построить её график.

2. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х.

Решение. По определению функция распределения F(x)=P(X<x). Если х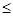1, то F(x)=0, так как значений, меньших единицы, случайная величина Х не принимает.

Если 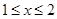, то F(x)=0,2. Действительно, Х может принять значение единицы с вероятностью 0,2.

Если , то F(x)=0,2+0,3=0,5. Действительно, Х может принять значение единицы с вероятностью 0,2 и значение два с вероятностью 0,3; следовательно, одно из этих значений, безразлично какое, случайная величина Х может принять с вероятностью 0,7(по теореме сложения вероятностей несовместных событий).

Если 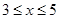, то F(x)= 0,2+0,3+0,4=0,9 (по теореме сложения вероятностей несовместных событий).

Если x>0, то F(x)=1, так как в этом случае событие является достоверным.

Следовательно функция распределения имеет вид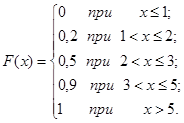

Построим график этой функции (рис. 7.1.).

Пример 7.2. Непрерывная случайная величина Х задана функцией распределения 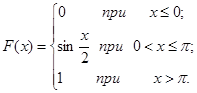Найти:

а) вероятность того, что в результате испытания Х примет значение, находящееся в интервале ;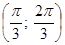

б) плотность распределения вероятностей f(x);

в) математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х.

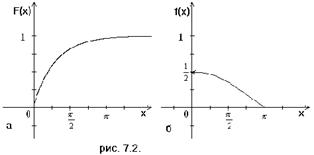
Построить график функций F(x) и f(x).

Решение. 1. Воспользуемся формулой 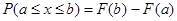, принимая , получаем.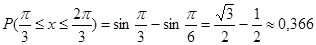

2. Плотность распределения вероятностей f(x) равна производной от функции распределения F(x): 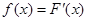. Следовательно,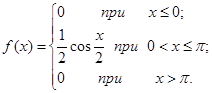

Поскольку все возможные значения случайной величины Х принадлежат интервалу (0; 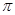), то, применяя формулу (7.3.), получаем 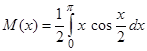. Интегрируя по частям, находим .

Дисперсию D(x) вычисляем по формуле (7.5.):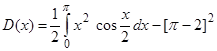

Выполняя дважды интегрирование по частям, находим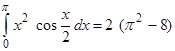

Окончательно получаем D(x)= .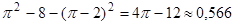

Среднеквадратическое отклонение .

Построим графики функций F(x) и f(x) (рис.7.2.).

Пример 7.3. Непрерывная случайная величина Х задана плотностью распределения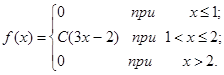

Найти: а) постоянный параметр С;

б) функцию распределения F(x).

Решение. А) плотность распределения f(x) должна удовлетворять условию 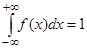. Попытаемся добиться того, чтобы это условие выполнялось для заданной функции 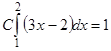. Так как 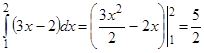, то ;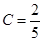

б) для нахождения функции распределения F(x) используем формулу(7.2.). Если 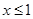, то .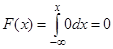

Если 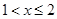, то .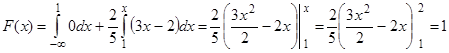

Следовательно, искомая функция распределения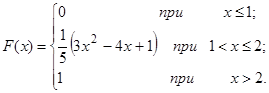

Задача 10. Дискретная случайная величина Х задана законом распределения (в первой строке таблицы приведены возможные значения, во второй – вероятности возможных значений). Требуется: а) построить многоугольник распределения; б) найти функцию распределения F(x) и построить её график; в) найти математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х.

10.1.	xi
pi	0,1	0,2	0,2	0,4	0,1
10.2.	xi	-3	-1
pi	0,1	0,2	0,4	0,2	0,1
10.3.	xi
pi	0,3	0,1	0,3	0,2	0,1
10.4.	xi	-4	-2
pi	0,1	0,2	0,3	0,2	0,2
10.5.	xi
pi	0,2	0,2	0,4	0,1	0,1
10.6.	xi	-2
pi	0,05	0,1	0,5	0,2	0,15
10.7.	xi
pi	0,1	0,4	0,25	0,15	0,1
10.8.	xi
pi	0,15	0,2	0,3	0,2	0,15
10.9.	xi	-1
pi	0,4	0,2	0,1	0,2	0,1
10.10.	xi
pi	0,1	0,2	0,3	0,25	0,15
10.11.	xi	-2	-1
pi	0,15	0,2	0,4	0,15	0,1
10.12.	xi	-2
pi	0,2	0,25	0,3	0,15	0,1
10.13.	xi
pi	0,05	0,3	0,4	0,15	0,1
10.14.	xi
pi	0,1	0,3	0,2	0,3	0,1
10.15.	xi	-2	-1
pi	0,15	0,2	0,3	0,25	0,1
10.16.	xi	-1
pi	0,1	0,15	0,35	0,3	0,1
10.17.	xi
pi	0,15	0,4	0,3	0,1	0,05
10.18.	xi	-3
pi	0,3	0,25	0,2	0,15	0,1
10.19.	xi
pi	0,15	0,2	0,3	0,25	0,1
10.20.	xi	-2	-1
pi	0,15	0,1	0,35	0,3	0,1
10.21.	xi
pi	0,1	0,2	0,4	0,25	0,05
10.22.	xi	-1
pi	0,1	0,15	0,3	0,25	0,2
10.23.	xi
pi	0,1	0,2	0,4	0,2	0,1
10.24.	xi
pi	0,15	0,3	0,25	0,2	0,1
10.25.	xi	-2
pi	0,15	0,25	0,3	0,2	0,1
10.26.	xi
pi	0,25	0,15	0,2	0,3	0,1
10.27.	xi	-1
pi	0,2	0,25	0,3	0,1	0,15
10.28.	xi
pi	0,1	0,3	0,2	0,1	0,3
10.29.	xi
pi	0,2	0,3	0,25	0,15	0,1
10.30.	xi
pi	0,1	0,15	0,35	0,3	0,1

Задача 11. Дискретная случайная величина Х может принимать только два значения: х₁ и х₂, причём х₁<х₂. Вероятность того, что Х примет значение х₁, равна р₁. Найти закон распределения случайной величины Х, если известны её математическое ожидание М(х) и дисперсия D(x).

11.1.	pi=0,2	М(х)=1,9	D(х)=0,16
11.2.	pi=0,4	М(х)=1,6	D(х)=0,24
11.3.	pi=0,8	М(х)=1,2	D(х)=0,16
11.4.	pi=0,3	М(х)=1,7	D(х)=0,21
11.5.	pi=0,9	М(х)=1,1	D(х)=0,09
11.6.	pi=0,5	М(х)=1,5	D(х)=0,25
11.7.	pi=0,1	М(х)=1,9	D(х)=0,09
11.8.	pi=0,6	М(х)=1,4	D(х)=0,24
11.9.	pi=0,7	М(х)=1,3	D(х)=0,21
11.10.	pi=0,2	М(х)=2,6	D(х)=0,64
11.11.	pi=0,4	М(х)=2,2	D(х)=0,96
11.12.	pi=0,8	М(х)=1,4	D(х)=0,64
11.13.	pi=0,3	М(х)=2,4	D(х)=0,84
11.14.	pi=0,9	М(х)=1,2	D(х)=0,36
11.15.	pi=0,5	М(х)=2,0	D(х)=1,00
11.16.	pi=0,1	М(х)=2,8	D(х)=0,36
11.17.	pi=0,6	М(х)=1,8	D(х)=0,96
11.18.	pi=0,7	М(х)=1,6	D(х)=0,84
11.19.	pi=0,2	М(х)=3,4	D(х)=1,44
11.20.	pi=0,4	М(х)=2,8	D(х)=0,16
11.21.	pi=0,8	М(х)=1,6	D(х)=1,44
11.22.	pi=0,3	М(х)=3,1	D(х)=1,89
11.23.	pi=0,9	М(х)=1,3	D(х)=0,81
11.24.	pi=0,5	М(х)=2,5	D(х)=2,25
11.25.	pi=0,1	М(х)=3,7	D(х)=0,81
11.26.	pi=0,6	М(х)=2,2	D(х)=2,16
11.27.	pi=0,7	М(х)=1,7	D(х)=1,89
11.28.	pi=0,9	М(х)=3,9	D(х)=0,64
11.29.	pi=0,3	М(х)=3,4	D(х)=0,84
11.30.	pi=0,1	М(х)=3,8	D(х)=0,36

Задача 12. Непрерывная случайная величина Х задана функцией распределения F(x). Найти: а) вероятность того, что в результате испытания величина Х примет значение, находящееся в интервале (a, b); б) плотность распределения вероятностей f(x); в) математическое ожидание, дисперсию и среднеквадратичное отклонение случайной величины Х.

Построить графики функций F(x) и f(x).

12.1.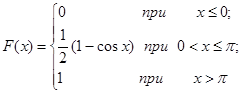
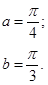
12.2.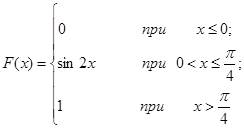
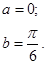
12.3.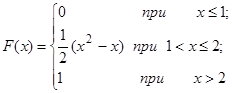
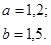
12.4.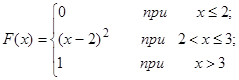
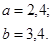
12.5.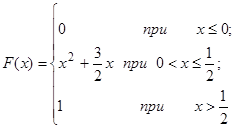
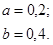
12.6.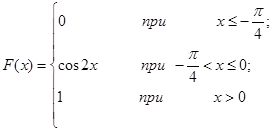
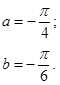
12.7.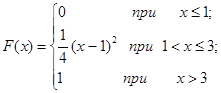
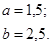
12.8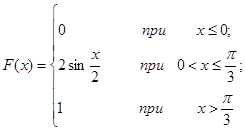
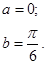
12.9.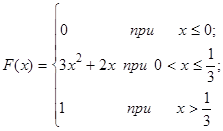
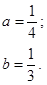
12.10.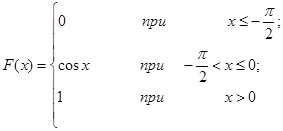
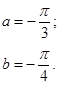
12.11.
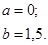
12.12.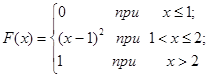
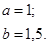
12.13.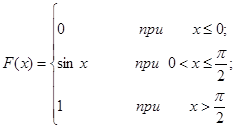
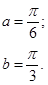
12.14.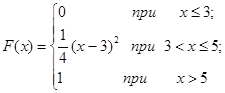
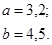
12.15.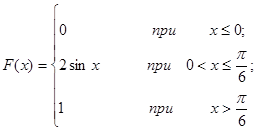
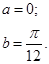
12.16.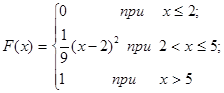
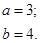
12.17.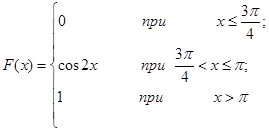
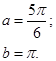
12.18.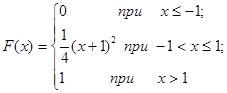
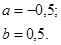
12.19.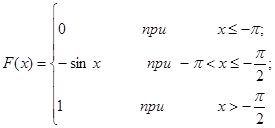
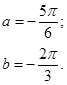
12.20.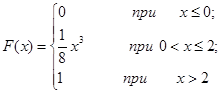
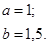
12.21.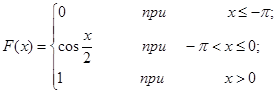
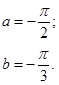
12.22.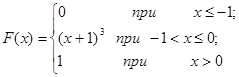
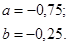
12.23.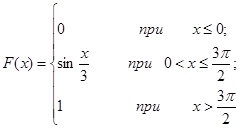
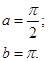
12.24.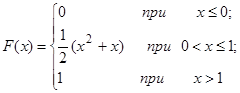
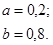
12.25.
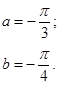
12.26.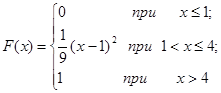
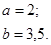
12.27.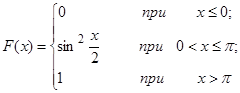
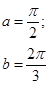
12.28.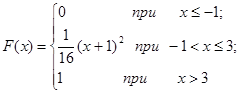
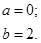
12.29.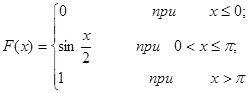
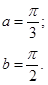
12.30.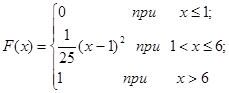

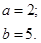
Задача 13. Непрерывная случайная величина Х задана плотностью распределения вероятностей f(x). Найти: а) постоянный параметр С; б) функцию распределения F(x). Построить графики функций F(x) и f(x).

Дата добавления: 2014-10-31